功率分配机构效率研究

不考虑搅油损失、润滑等因素的影响，直齿啮合齿轮副的啮合效率经验公式［108］可表示为：

式中，η表示效率，Za和Zb为两啮合齿轮的齿数，正、负号分别对应着外啮合和内啮合，下标ab表示功率由a流入b。本书在计算时为了简便分别将内外啮合效率取为0.98和0.97。

ηi0j定义为行星架固定时的简单行星排齿轮的效率：

ηi0j=ηiq ·ηqj

注意：齿轮副的啮合效率与观察者所处的参考坐标系（固定于行星架上）无关，作用于太阳轮、齿圈和行星架的转矩始终满足转矩平衡方程：

Ti ＋Tj ＋Tk=0

假设行星架固定，则各元件之间的相对转速为

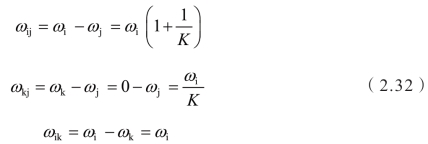
主动件：太阳轮。被动件：齿圈。固定件：行星架。

得到

主动件：齿圈。被动件：太阳轮。固定件：行星架。

得到

主动件：太阳轮。被动件：行星架。固定件：齿圈。此时效率

齿圈固定，由转速方程可得

则太阳轮与行星架的相对转速为

ηj（i－k）可改写为

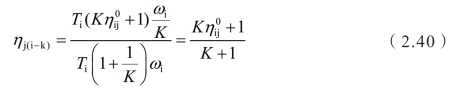
主动件：行星架。被动件：太阳轮。固定件：齿圈。

效率可转换为

主动件：齿圈。被动件：行星架。固定件：太阳轮。

由于太阳轮固定，可得

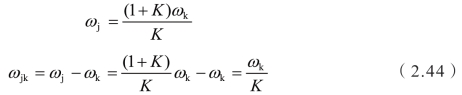
效率可转换为

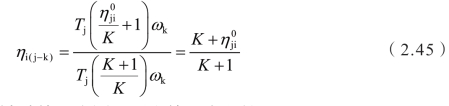
主动件：行星架。被动件：齿圈。固定件：太阳轮。

由于太阳轮固定，可得

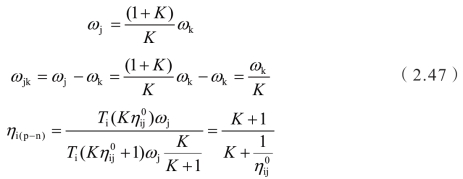
对于具有二自由度的基本行星排，单个元件p的绝对旋转角速度可以表示为另外两个基本元件m，n的绝对旋转角速度的线性组合：

如图2.20所示，有两种可能的功率流向：双输入、单输出和单输入、双输出。对双输入、单输出情况，假设功率由基本元件m，n流入基本行星排，ηe为行星排效率，则有

图2.20　二自由度行星机构功率示意

若假设

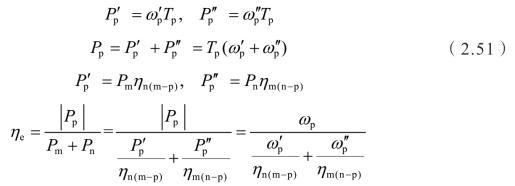
对于单输入、双输出的情况，有

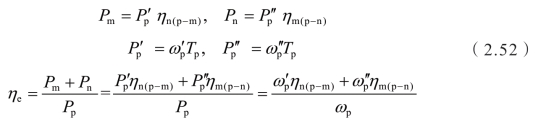
二自由度行星排系统效率见表2.4。

表2.4　二自由度行星排系统效率

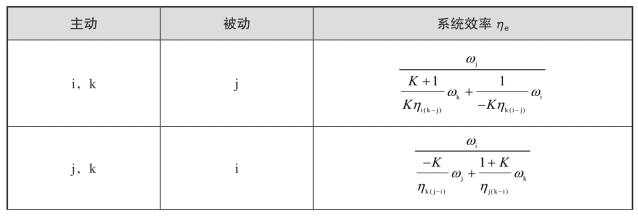
续表

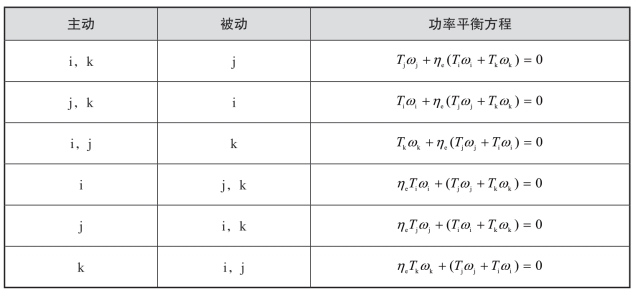
二自由度行星排功率平衡方程见表2.5。

表2.5　二自由度行星排功率平衡方程

需要注意，图2.21中的效率模型仅对应于电池功率接近于0的情形，意味着一个电机作为电动机时，另一个电机则充当发电机，而二者电功率实现平衡。

此时电动机的用电功率和发电机的充电功率均被认为发动机输入功率的函数：(www.xing528.com)

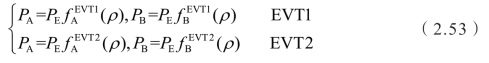
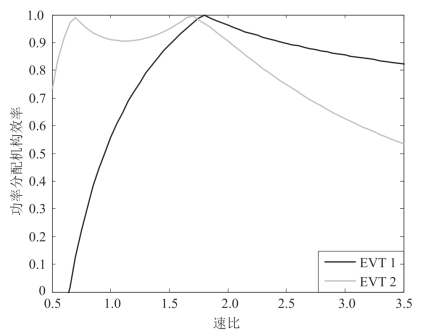
图2.21　功率分配装置效率

若不考虑行星排机械损失，则定义功率分配机构的效率如下：

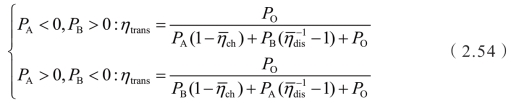
式中，ηtrans为功率分配机构效率；PA，PB分别为电机A、B功率；PO为输出功率，PE为发动机功率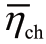；，分别为电机作为发电机、电动机工作时的平均效率；f是一个与速比相关的功率分流系数，由功率流分析得到，不同速比下的耦合机构效率曲线如图2.22所示。

考虑行星排机械损失，则利用行星排功率流、单自由度和二自由度效率分析方法，集成分析由多个简单排组合而成的功率分配装置的效率。本节的分析基于一个基本假设：功率流分析中未计入的损失不会影响行星耦合机构的功率流向和分流形式。对于某个基本行星排，根据功率流分析的结果，得到基本行星排的主、被动件和功率流向，在表中选取合适的表达式，结合转速方程和转矩方程，可得到如下的功率方程。

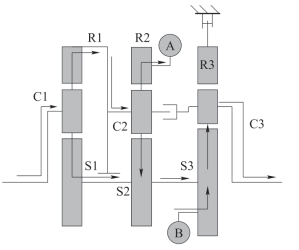
图2.22　EVT1功率流情况

（ρEVT1＞1.787 9）

α，β归纳于表2.6。

表2.6　功率方程系数

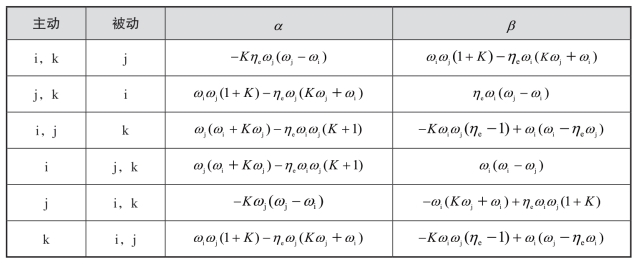
集成分析过程如下：

（1）根据功率分配机构的构型进行运动学分析。

（2）进行功率流分析（不考虑机械效率）。

（3）在得到功率流方向后，由表4、表5、表6获得对应的功率平衡方程、所需的效率值及系数值。

（4）对于每个连接节点，写出功率平衡条件。

（5）确定系统的功率输入点和输出点，可定义输入功率分别为，输出功率则分别为。

（6）求解出各个行星排元件以及各连接点的功率平衡方程。

（7）所得的输出功率之和与输入功率之和的比例即为系统总效率。

以ρEVT1＞1.787 9的流程为例说明分析效率的步骤：首先根据运动学与功率流分析得到各行星排的主、被动件情况：

行星排1：主动件为行星架，被动件为齿圈和太阳轮，因此有

ηe1Tk1ωk1 ＋(Tj1ωj1 ＋Ti1ωi1)=0

式中，

式中，

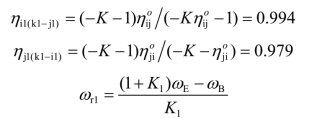
列功率方程：

αPs1 ＋βPr1=0

式中，

此外，有

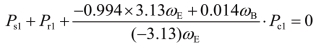
行星排2：主动件为行星架，被动件为齿圈和太阳轮，因此有

ηe2Tk2ωk2 ＋(Tj2ωj2 ＋Ti2ωi2)=0

式中，

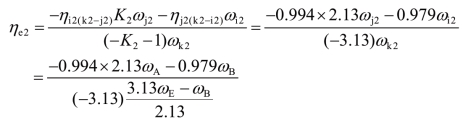
列功率方程：

αPs1 ＋βPr1=0

式中，

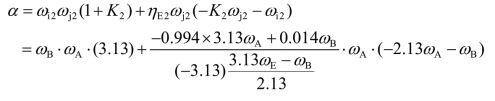
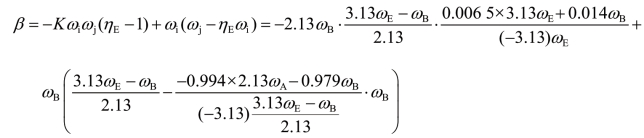
此外，有

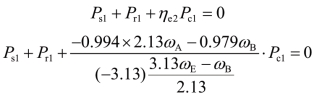
行星排3：主动件太阳轮，被动件行星架，有

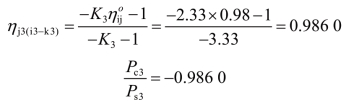
最后，列出各连接件的功率平衡方程组：

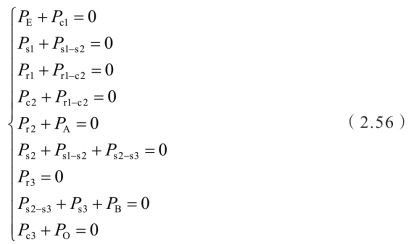
求解方程组，输出功率与输入功率的比例即为系统总效率，其他模式的其余情况也按照类似的流程求解得到，最终获得的系统效率如图2.23所示。

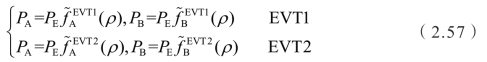
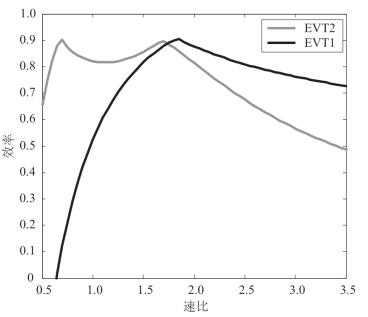
图2.23　考虑机械效率后的功率分配装置效率

若将功率分配机构的机械损失分别集中等效到电机处和输出端，则可将式改写为功率分配装置的效率包括电功率损失和机械功率损失，由于功率分配装置的机械损失，转矩方程式中的系数矩阵中的各元素实际上均为变量，但为了能够使得本书第三章中进行能源效率最优化策略设计时将转速、转矩表达式中的系数矩阵保持为线性定常，进而提高优化求解过程的计算效率，将图2.23和 图2.21在各速比下的效率结果相除，将功率分配机构的机械效率（不包括电机效率）简化为一个等效平均机械效率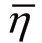（本书求得的效率取平均值为0.902），将机械损失计入实际的功率输出项：

功率分配装置效率为

式中，ηtrans为图2.21中未考虑机械损失的功率分配装置效率。