当从动件运动规律确定以后，凸轮轮廓曲线便可用解释法求解，也可用作图法绘制。对精度要求不很高的凸轮，一般采用作图法即可满足使用要求，而且较简便。本节仅研究如何用作图法绘制凸轮的轮廓曲线。
1）作图法的原理
为便于绘出凸轮轮廓曲线，应使工作时转动着的凸轮与不动的图纸间保持相对静止。根据相对运动原理，如果给整个凸轮机构加上一个与凸轮转动角速度ω 数值相等、方向相反的“-ω”角速度，则凸轮处于相对静止状态，而从动件一方面按原定规律在机架导路中作往复移动，另一方面随同机架以“-ω”角速度绕O点转动，即凸轮机构中各构件仍保持原相对运动关系不变。由于从动件的尖底始终与凸轮轮廓相接触，因此，在从动件反转过程中，其尖底的运动轨迹，就是凸轮轮廓曲线（见图2.41）。这就是凸轮轮廓设计的反转法原理。
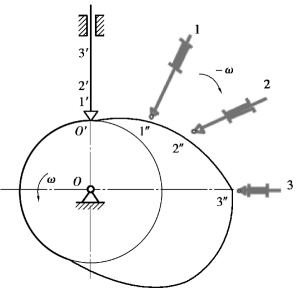
图2.41 反转法原理
根据反转法原理，设计时可将凸轮视作不动，分别作出从动件在反转运动过程中边反转边沿导路移动时尖底的轨迹。光滑连接这些点，即得要求的凸轮轮廓曲线。
2）凸轮轮廓曲线的设计
（1）对心式直动尖底从动件盘形凸轮轮廓的设计
已知凸轮的基圆半径rb、角速度ω 和从动件的运动规律，设计该凸轮轮廓曲线。
设计步骤：
①选比例尺μl，根据从动件的运动规律，作出从动件的s-φ（t）线图，如图2.42所示。
图2.42 对心式直动尖底从动件盘形凸轮轮廓的设计
②用与s-φ（t）线图相同的长度比例尺，以rb为半径作基圆，此圆与从动件移动导路中心线的交点A，便是从动件尖底的初始位置。
③自OA 开始，沿“-ω”方向，在基圆上取Φ，Φs，Φ′，
，并将其分成与s-φ（t）线图中相应的等分，得1，2，3，…各点，则O1，O2，O3，…，这一系列向径线的延长线，就是从动件在反转过程中的导路位置线。
④在从动件各个位置线上，自基圆向外分别量取11′=11′，22′=22′，33′=33′，…，由此得1′，2′，3′，…各点，这就是从动件反转过程中其尖底所处的一系列位置。(www.xing528.com)
⑤将1′，2′，3′，…各点，用曲线板连成光滑的曲线，该曲线即为所求的盘形凸轮的轮廓曲线。
（2）对心式直动滚子从动件盘形凸轮轮廓的设计
已知凸轮的基圆半径rb、角速度ω、滚子半径rT和从动件的运动规律，设计该凸轮轮廓曲线。
设计步骤：
①将滚子中心看成尖底从动件的尖底，按照上述方法先绘制出尖底从动件的凸轮轮廓曲线（即滚子中心的轨迹），如图2.43所示，该曲线称为凸轮的理论轮廓曲线。
②以理论轮廓曲线上的各点为圆心，以滚子半径rT为半径作一系列的滚子圆。然后再作这些滚子圆的内包络线即为凸轮的实际工作曲线，该曲线称为凸轮的实际轮廓曲线。
应当指出，在绘制滚子从动件凸轮机构的凸轮轮廓曲线时，其滚子从动件的凸轮基圆半径是指其理论轮廓曲线的最小向径；理论轮廓曲线与实际轮廓曲线是两条法向等距曲线。
（3）对心式直动平底从动件盘形凸轮轮廓的设计
已知凸轮的基圆半径rb、角速度ω 和从动件的运动规律，设计该凸轮轮廓曲线。
设计步骤：
①把平底与从动件轴线的交点看成尖底从动件的尖底，按照前述方法，求出尖底的一系列位置点1′，2′，3′，…。
②再过这些位置点1′，2′，3′，…画出其平底一系列位置线，这一系列平底位置线的包络线即为所求的凸轮实际轮廓曲线，如图2.44所示。
图2.43 滚子从动件盘形凸轮轮廓
图2.44 平底从动件盘形凸轮轮廓
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
