优化翅片间距，提高散热效率

11.3.1.1　翅片传热理论分析

对于两相邻的对称等温平板，前人得到了如下半经验关系式［6，7］：

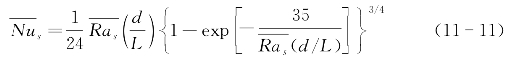
其中，Nus 为平均努塞尔数，Ras为瑞利数，d为平板间距，L为平板长度。式（11-11）为以空气为工作流体得到的关系式，其应用范围为：

式（11-11）中，平均瑞利数分别定义为：

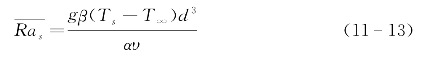
当d≪L时，式（11-11）可以简化为：

对于空气而言，考虑翅片温度为70℃的等温体，环境温度为20℃，此时按照平均温度Tf=45℃时，空气的参数［8］为：υ=17.70×10-6m2／s，Pr=0.702，β=翅片节距s为8 mm，当翅片厚度为0.8 mm时，则翅片间距d为7.2 mm。

由式（11-13）可计算得出：

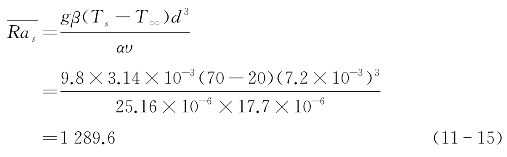
因此，翅片之间的自然对流为层流边界层。此处

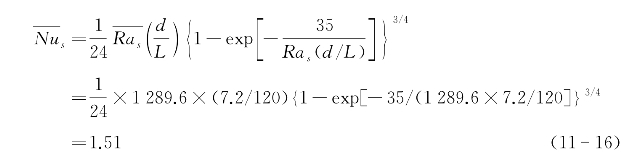
翅片内侧面对流传热的特征尺寸D=A／P=40 mm。

由此，理论平均对流换热系数为

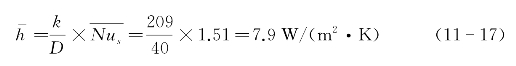
由式（11-12）可以得出s的范围为：(www.xing528.com)

1.3 mm＜s＜43 mm

此时，由式（11-15）和（11-16）可得理论平均对流换热系数为：

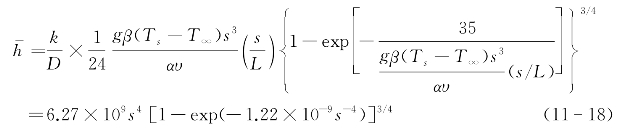
考虑当翅片间距d在4～12 mm之间时，理论平均自然对流换热系数如图11-2所示。

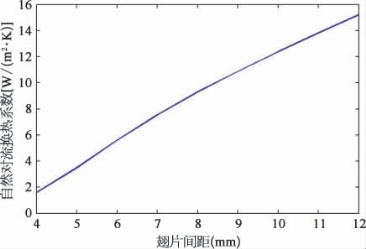
图11-2　理论对流传热系数与翅片间距的关系

值得注意的是，在以上理论计算中，并未考虑管道存在的影响，同时没有考虑到在实际中翅片并非为一等温体，但这样的计算值也为数值模拟提供了一定的参考。

11.3.1.2　数值优化分析

采用Ansys Icepak进行数值模拟，该软件由计算流体力学软件商Fluent公司研发，广泛用于电子热分析、结构热分析等领域。如图11-3所示，从整个散热器中截取一个翅片散热单元进行讨论，该单元由2个240 mm×120 mm×0.8 mm的翅片和3段外径为10 mm铜管组成。翅片材料设置为6063-T5铝，重力方向沿着y轴方向，给定环境温度为20℃，铜管表面温度恒温70℃。整个系统4个开口处为开口边界条件，开口处为环境温度和环境压强。采用单精度、一阶迎风格式进行计算。由此，铜管表面的热量经翅片传到空气中，引起翅片内部空气的密度差，从而诱发空气流动，产生自然对流换热。通过改变不同的翅片节距，经计算后、后处理可以获得不同节距下翅片内表面上的平均自然对流换热系数［1］。通过选取一个合适的平均自然对流换热系数，即可确定相应的翅片节距。

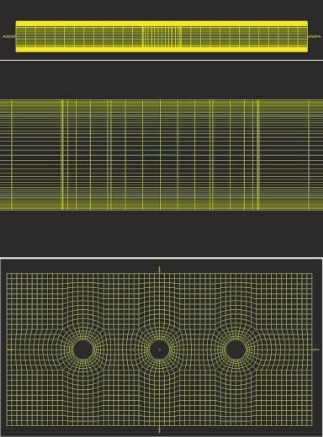
图11-3　翅片计算网格

通过Icepak网格产生器，设置网络类型为Hexa Unstructured，x、y、z上的网格大小分别为0.005 mm、0.004 mm、0.004 mm，产生的网格如图11-3所示，网格数量在80 000～12 000之间。通过网格检查工具，可知：网格倾斜程度数值Skewness在0.75～1之间，网格单元接近等边的程度很好；面对齐Face alignment数值接近1，表面不存在严重变形的单元；网格质量在0.8～1之间，网格扭曲程度很小；网格体积大于e-12，满足单／双精度的求解要求。经计算对比不同网格数的模拟结果，满足网格无关性要求，如图11-4所示。

按照LED高杆灯长期作业、性能稳定的系统需求，无风扇的翅片散热器是唯一较为合理的散热方式［1］。但是，相对于风扇冷却，纯粹的自然对流的表面传热系数一般较低［＜10 W／（m2·K）］。经处理后数据可以得到翅片表面的平均自然对流换热系数与翅片节距的关系，如图11-5所示。当翅片节距为4、6、8、10、12 mm时，对应的翅片表面平均自然对流换热系数分别为：0.56、2.89、4.87、6.07、6.62 W／（m2·K）。然而，假定初始液态金属管路长度为420 cm时，随着不断增加翅片的节距，两个翅片之间所需求的液态金属管路的长度也随之加长，由此造成了液态金属填充量的增加。此外，采用较大的翅片节距，设计出来的液态金属散热器整体体积也将随之增大，造成散热器重量变大，不利于高杆灯的高空安装及稳定性。综合考虑这些因素，本章案例选取翅片节距8 mm作为合适的翅片节距进行散热器结构设计，此时翅片表面平均自然对流换热系数为4.87 W／（m2·K）。

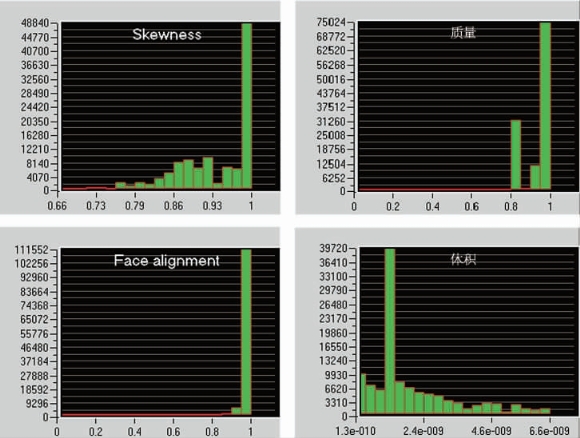
图11-4　网格质量相关数

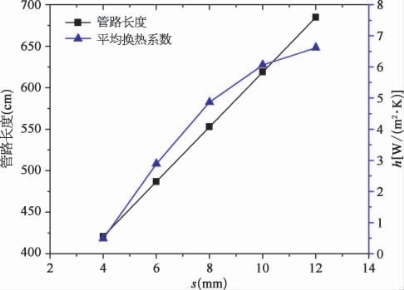
图11-5　翅片节距s对表面平均自然对流换热系数h以及管路长度的影响