圆管内液态金属流体换热理论探究

圆形管道内液态金属流动过程满足的控制方程为：

此处，ar，ax分别为液态金属径向和轴向的热扩散系数，为简便起见，可以假设：

边界条件可以设定为

稳态时，则式（8-2）变为：

变换为无量纲形式为：

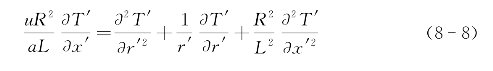
式中，由分离变量法，可得到方程（8-8）的稳态解。为简化起见，在下列分析中，略去无量纲方程（8-8）中的上标′。

假定无量纲温度可表示为T（r，x）=R（r）X（x），则方程（3-7）变为：

方程（8-9）中，等号左边为x的函数，右边为r的函数。要使两边相等，其值必须为一个常数。在方程（8-9）中，只有这个常数小于零才有非零解，因而设这个常数为-β2，则方程（8-9）分解为：

考虑物理条件，可以得到方程（8-10）的特征值为：

方程（8-11）为贝塞尔方程，其根为：

式中，βm由边界条件决定，对第一类边界条件βm=0，也依然是方程的根。

考虑相同的边界条件式（8-4）～（8-6），可得到液态金属流动传热过程温度分布的理论解为：

由Peclet数式（8-14）可简化为

边界上能量方程可写为：(www.xing528.com)

式中，h为对流换热系数，Tm为横截面积上流体平均温度，对圆管可表示为

考虑无量纲参数以及Bessel函数关系式，

可以从方程（8-9）到（8-12）得到局部Nu数Nux

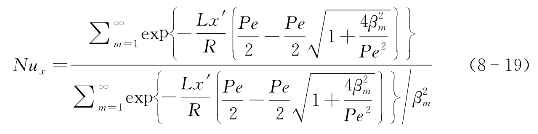
如果忽略轴向导热，则方程（8-2）到（8-6）可得解析解为：

由局部Nu数在流道长度上积分，可得到流道的平均Nu数，即：

由式（8-19）和（8-21）可知，Pe数对液态金属的换热起着重要作用，这与之前的研究是一致的［4］。显然

因此，当Pe数足够大时，轴向导热可以忽略，对分析结果造成的影响不大，而当Pe数很小时，忽略轴向导热将带来较大误差。图8-1到图8-5分别给出了考虑轴向导热和忽略轴向导热时，管道R／L，x／L，Pe数对无量纲分布，以及局部Nu数的影响。

图8-1　考虑轴向导热与忽略轴向导热时的无量纲温度分布

（a）x=0.05，Pe=10；（b）x=0.1，Pe=10。

图8-2　R／L=0.05时不同位置时的相对误差与Pe数的关系

图8-3　当R／L=0.01，x／L=0.01时Nu数与Pe数的关系

图8-4　Nux与R／L的关系（x／L=0.01）

图8-5　Nux与x／L的关系（R／L=0.04）