电磁泵驱动系统的仿真分析

7.3.3.1　计算物理模型

直流电磁泵的结构相对简单，图7-10是两种具有不同结构流道的电磁泵的示意图［21］。根据电磁泵的工作原理，在磁场作用区域内电磁泵的截面形状需做成扁平状［3］，磁铁间隙可设为1 mm。为了同外管路的连接，在电磁泵的进出口设置了圆形的引接管。在电磁泵1中，液态金属流体受到扁平工作段的电磁力推动作用后直接从圆形的引接管流出；而在电磁泵2中还包括了位于工作段和引接管之间的过渡段，此段将工作段的扁平截面平滑地过渡到引接管的圆形截面。

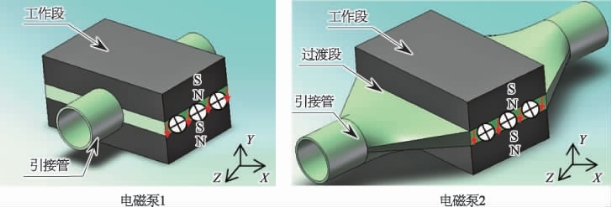
图7-10　两种不同流道结构的电磁泵示意

考虑到液态金属电磁泵流道的高度相比其长度和宽度要小，因此对于直流电磁泵驱动下的液态金属可作二维流场简化处理，如图7-11所示。在电磁泵的入口设置速度边界条件，出口为压力边界条件，电极壁面设为电压的边界条件，剩余壁面均设置成无滑移的绝缘壁面边界条件。

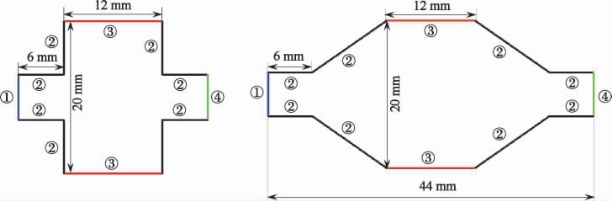
图7-11　计算区域及边界条件

①速度入口边界条件；②绝缘壁面边界条件；③电压边界条件；④压力出口边界条件。

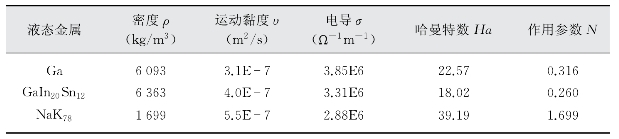
表7-1给出了电磁泵仿真计算过程中的参数取值。在计算中，忽略永磁体的边界效应，假设永磁体所产生的磁场均匀地分布在电磁泵的工作段。数值求解采用压力校正算法，先假设一个压力场，然后通过求解不可缩流动的N-S方程得到速度场，这些速度不需要满足泊松型连续方程，所以对压力场的修正也带来了速度场的修正，最终满足质量守恒。求解速度场的同时计算电势场的方程，得到安培力，然后将其反馈回N-S方程并作为体积力处理，连续耦合安培力和速度场，直到牛顿迭代收敛。

表7-1　计算参数取值表［14］

7.3.3.2　仿真结果

如下介绍以镓为流动工质，在入口速度为0.1 m／s，分别在没有外加电磁场和施加了1T磁场、20 m V电压的条件下，对上述两种流道结构的电磁泵的速度矢量进行仿真计算的结果［21］。从图7-12可以看出，在无外加电磁场的情况下，电磁泵1和2中靠近管壁的流体质点的流速均比较小；但当在流道外加了电磁场，流体在进入电磁泵的工作段后，速度分布发生了扭曲（图7-13），在靠近电极壁面附近的流体速度要比其他区域都明显要大，在电磁泵1中甚至还出现较为明显的漩涡。图7-14给出了电磁泵流道的电流矢量分布，电流密度矢量由两部分组成，一部分是由电极静电场产生，另一部分是由感应电动势场产生。从图7-14可以看出，电流从高电势壁面往流场区域里扩散，最终又汇集到低电势壁面，在两电极壁面附近的电流最大。由交叉电流密度和磁场强度产生的安培力在靠近电极的地方最强，使得这里比其他区域的轴线速度阻力更小，所以才产生了如图7-13的速度矢量分布。图7-15是电磁泵1和2进出口压差的对比图。从图中可以得到在相同入口速度和电磁场作用下，电磁泵1的进出口压差要比电磁泵2小。这是因为在电磁泵1中，液态金属经扁平状的工作段区直接流到圆形引接管，在边壁突变的地方，容易出现主流与边壁脱离的现象形成漩涡区，造成较大的阻力损失。

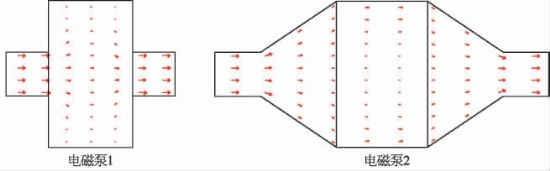
图7-12　无外加电磁场的电磁泵流道速度矢量

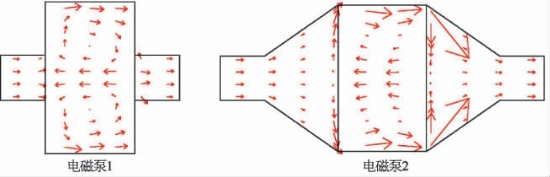
图7-13　1 T磁场、20 mV电压下的电磁泵流道的速度矢量

图7-14　电磁泵流道的电流分布

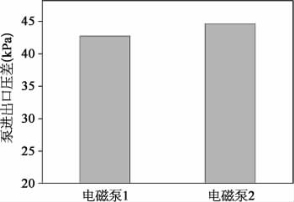
图7-15　不同流道结构的电磁泵的进出口压差(www.xing528.com)

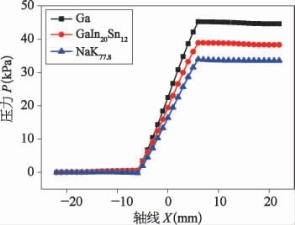
图7-16　不同流动工质的泵的轴线压力分布

液态金属镓或其合金由于价格会使其利用受到一些限制，共晶合金NaK77.8的熔点可以达到-12.65℃，其导热系数为21.8 W／（m·K），加上碱金属材料的易得性，考虑到芯片冷却的载冷工质是预先密封在管路里的，若能把共晶钠钾合金作为芯片散热的冷却工质，则不仅会有良好的散热性能，同时其成本又极为低廉［21］。为此，这里以电磁泵2为例，分别对用镓、镓铟锡和钠钾合金作为流动工质的电磁泵性能进行了数值仿真。图7-16是3种工质在入口速度为0.1 m／s和施加了1 T磁场、20 m V电压的条件下的电磁泵的轴线压力图。从图中可以看出流体从入口进入电磁泵的工作区域，轴线压力得到逐步的提升。在这3种工质的对比中，液态金属镓的电磁泵出口处压力值最大，这是因为液态金属镓的大电导值使得其在相同的输入电压下，能产生比较高的电流和电磁力，进而获得较大的出口压力。

当电磁泵流量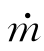=0的情况下，电磁泵的压头与电磁场有着如下关系［4］：

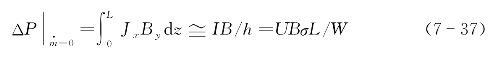
式中，Jx为电流密度，By为磁场强度，L为处于磁隙间的液态金属的长度，h为电极的宽度，W为电磁泵流道的宽度，σ为液态金属的电导，U为电极壁面的输入电压。基于上述理论公式，这里给出了以镓为工质，外输电压为4 m V的电磁泵2的静压头同外加磁场的变化关系，以及外加1 T磁场的电磁泵2的静压头同外加电压的变化关系，结果如图7-17和7-18所示。从图中可以看出，仿真值与解析解几乎完全重合，进一步表明液态金属电磁泵的进出口压差同磁感应强度和外加电压呈线性变化关系。

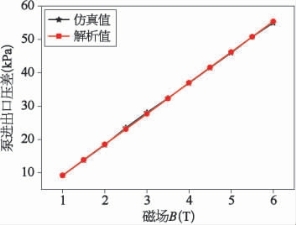
图7-17　电磁泵2的压头同外加磁场的变化关系

图7-18　电磁泵2的压头同外加电压的变化关系

7.3.3.3　实验对比

为验证仿真计算结果的准确性，考虑到电磁泵2具有较为合理的流道结构，笔者实验室采用浇注的办法制作了电磁泵2并进行了相应的实验测量［21］。首先用石蜡等熔点较低的材料固化定型成预先设计好的流道形状，此流道应包含具有扁平截面的工作段，将上述定型后的流道置于模具内部，并将圆形引接管接入到上述流道的两端。电极材料由导电性能良好的铜板制成，厚度为1 mm，电极从两侧嵌入到流道的扁平状部分。在浇注过程中，使用环氧树脂作为材料，将用于形成泵体的液态浇注材料送入到模具内，待其填满后置于烘箱进行固化。浇注材料固化后，将模具和石蜡清除，在工作段区域安装永磁铁布置磁场。为了更为有效地利用永磁铁所产生的磁场，采用防漏磁材料2Cr13制作成导磁环，将电磁泵安放在导磁环内，可起到很好的防漏磁效果。

泵的进出口静态压差是电磁泵的主要性能指标之一，反映电磁泵对液态金属的驱动能力。图7-19给出了电磁泵静压实验的系统示意图。为便于观察和计量，使用透明的塑料软管同电磁泵连接形成U型管路。通过观察U型管左右两管内液面的高度差来感知泵进出口压强的大小，高度差越大，说明泵的进出口压差越大。

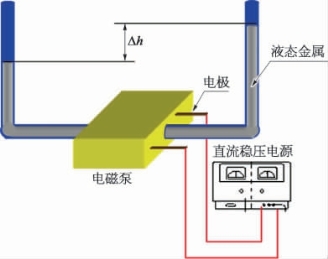
图7-19　电磁泵静压实验系统

U型管左右两边的高度差与电磁泵产生的静压头的关系式为：

式中，Δh是泵高，单位是m；ΔP静压是电磁泵产生的静压头，单位Pa；ρ是液态金属的密度，单位是kg／m3。

图7-20　不同输入电流下电磁泵静压随输入电流变化的实验值与仿真值

以GaIn20Sn12为流动工质，通过直流稳压电源给电磁泵的电极输入任意固定电流I，测量U型管的进出口高度差，拟合出电磁泵的静态压差与输入电流的变化关系，并与仿真计算结果比较。图7-20是在不同输入电流下，电磁泵2的静压随输入电流变化的实验值与仿真值。从中可以看出，实验值与仿真值吻合得比较好，但实验值要比仿真值小，这是因为在电磁泵的实际工作过程中还存在更多客观影响因素［21］，如：电枢效应、漫流损失等可能消耗电磁力产生的部分压头。实验和仿真结果均表明，上述两种流道结构的电磁泵在磁感应强度不变的情况下，静压头与通过液态金属的电流呈线性关系，因此可以通过调节电流的大小来改变电磁泵的驱动力。