低熔点金属热沉模块的数值传热模型

6.5.3.1　简化数值模型

数值模拟是指导热沉设计和优化的重要工具，建立低熔点金属相变热沉数值传热模型对于促进其应用十分重要。对于传统的有机类相变热沉，自然对流往往对强化相变材料内部的热量传递起着关键作用，因此在建模时需要将液相自然对流传热考虑进来。然而，对流的引入会极大地增加数值计算的计算量，特别是在三维模拟情形，可能导致计算耗时巨大。

如前所述，对于低熔点金属相变传热过程，其Ra数一般较小，热传导占主导地位，而自然对流传热可以忽略。因此，可以给出一种简化的数值计算模型来描述低熔点金属相变热沉的相变传热过程［11，15，16］。在简化模型中，忽略液相金属区域的自然对流及相应的自然对流传热，将整个相变材料区域视为静止的热传导区域来看待，这样一来便可以消除因求解非线性流动方程带来的困难。

这里，针对上一小节的EBiInSn热沉建立其简化三维传热模型。鉴于热沉模型的对称性，计算时只取其1／4进行模拟。图6-18是＃1 EBiInSn热沉的数值计算模型，＃2和＃3是类似的。模型包含3个部分：模拟热源、热沉结构、相变材料。为方便建模，这里将加热棒等效为热源底部的恒定热流。由于实验监测的是热沉底部的温度，而不是热源的温度，因此热源与热沉之间接触热阻可以不考虑，对结果影响不大。如果要考虑界面热阻的话，导热膏的热导率约为1 W／（m·K），厚度假定为0.1 mm，因此界面热阻可以设定为0.1×10-3m2·K／W。热沉的外侧与周围空气之间存在自然对流传热和热辐射，等效对流传热系数假定为10 W／（m2·K），环境温度为24℃，模拟热源周围视为绝热。

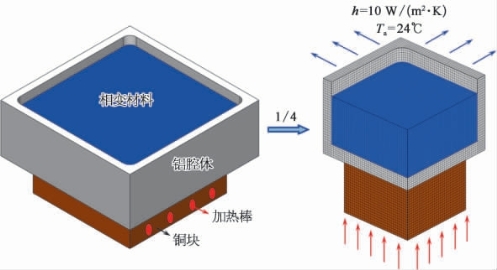
图6-18　＃1 EBiInSn热沉数值计算模型与网格划分

整个计算区域可以用下面的能量方程来描述：其中，H表示总焓，它包含显热焓Hs和潜热焓Hl两部分。这里，潜热焓Hl仅对EBiInSn区域有意义，对于模拟热源和铝腔体结构区域，其潜热焓始终为0。q为体积热源，在这里设为0。

6.5.3.2　数值模型的验证(www.xing528.com)

基于上述简化数值传热模型，采用ANSYS Fluent来进行数值计算。在正式计算之前，先进行了网格和时间步长无关性验证。以＃1 EBiInSn热沉为例，在80 W加热功率下，不同网格大小和时间步长下其有效工作时间计算结果如表6-9所示。可以看到，网格大小为13 022，时间步长为1 s时对于这一问题已足够精确。

表6-9　网格大小和时间步长无关性验证（＃1 EBiInSn，80 W）

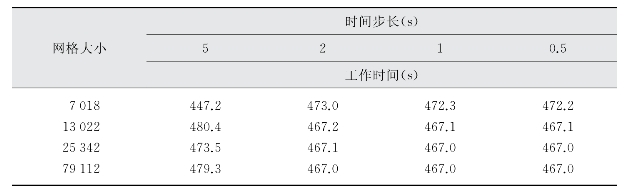
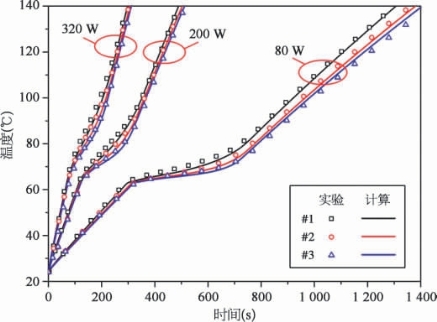
图6-19　数值计算结果与实验结果对比

这里，给出了＃1、＃2、＃3号EBiInSn热沉在80 W、200 W、320 W功率下的瞬态热性能计算结果，并对热沉底部平均温度进行了统计，如图6-19所示。可以看到，对于这9种工况，数值计算结果均与实验结果很好地吻合，这表明简化的数值传热模型可以很好地预测低熔点金属相变热控模块的传热过程。图6-20直观地展示了＃1 EBiInSn热沉在相变过程中的温度云图和液相分数云图。固相EBiInSn就像一个巨大的冷池，持续从热源吸热，而其温度始终保持在熔点值附近，直到完全熔化。液相EBiInSn内部的温度梯度是热沉底部温升的主要原因。基于这里给出的简化数值计算模型，也可以对其他结构形式和热边界条件情形进行快速的热性能模拟计算。

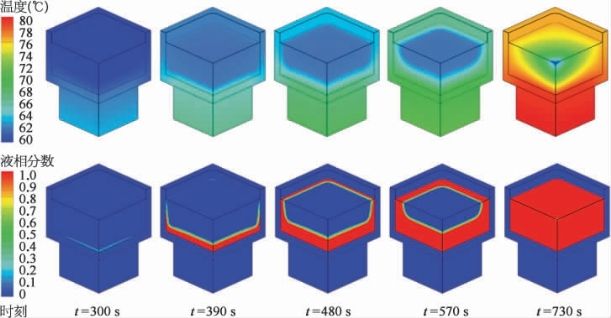
图6-20　＃1 EBiInSn热沉温度云图与液相分数云图（80 W热冲击）