腔体内低熔点金属相变传热的通用规律

由于低熔点金属相变材料的热物性质与传统的有机类相变材料存在很大不同，因此其固液相变传热过程也会有自身的特点。实际应用中，相变材料往往需要封装在腔体内。为此，如下对矩形腔体内的低熔点金属熔化过程进行讨论［11，15，16］。

6.4.2.1　数值计算模型的验证

在6.4.1小节中介绍了焓-多孔度方法的数学模型。基于这一模型，可以利用商用软件Ansys Fluent来对低熔点金属的熔化过程进行分析。在参数化研究之前，需先对数值计算模型的可靠性和精确性进行验证。Beckermann和Viskanta［17］曾对腔体内金属镓的熔化过程进行过定量实验测试研究。实验中，采用的腔体的长和宽均为47.6 mm，深度为38.1 mm。腔体左侧施加一个高于镓熔点（29.78℃）的恒定温度TH，腔体右侧则施加一个低于其熔点的恒定温度TC；其余4个面做绝热处理。初始时刻，用低温TC冷却整个相变材料区域，使其处于固态并且处于均匀的温度TC。当在左侧面施加高温TH后，左侧的镓开始熔化，液固界面逐渐向右移动并最终达到稳态，形成一个稳定的界面。实验中研究了5种不同的工况，见表6-4。

表6-4　方腔内镓熔化实验工况［17］

这里，将实验对应的问题简化为一个二维方腔（47.6 mm×47.6 mm）内的熔化问题，左右边界均为恒壁温条件。利用Boussinesq假设来激活液相区域的自然对流。由于所分析问题的Ra数低于自然对流的层流／湍流转变临界值109［11］，因此采用层流流动模型。图6-3展示了对＃1的数值计算结果，并与相应的实验数据做了对比。这里，选取时间为50 min时的结果，此时整个传热过程已经达到稳态。可以看到，在液态金属液相区域，温度分布呈现水平分布，这是典型的自然对流下的温度分布。在实验测试中，监测了3条水平线上的温度。将数值模拟得到的结果中的对应位置的温度分布与实验结果对比，如图6-3（b），可以看到，两者吻合较好。同时，也对另外4组实验工况进行了模拟计算，并获得其稳态时的固液界面位置，与实验结果对比，见图6-4。可以看到，两者也吻合较好，说明数值计算模型可以很好地预测低熔点金属的对流型熔化过程。

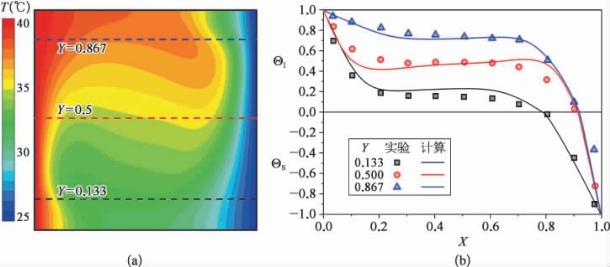
图6-3　数值计算结果与实验数据［17］对比

（a）温度云图，＃1，t=50 min；（b）3条水平线上的温度分布。

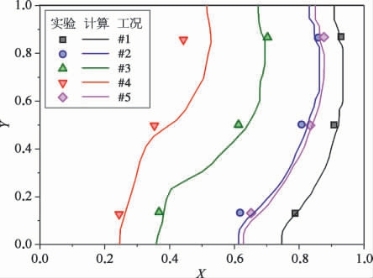
图6-4　稳态情况下固液界面位置

6.4.2.2　低熔点金属与有机相变材料熔化过程对比

为直观说明低熔点金属与传统有机相变材料固液相变传热过程的差别，选取典型的低熔点金属镓和典型的有机相变材料二十烷，两者的主要热物性数据对比见表6-5。假定有一个竖直腔体（5 mm×20 mm），初始时刻整个腔体和相变材料均处于熔点温度Tm，腔体左侧突然施加一个恒定的高温热源TH（TH=Tm+15℃），熔化过程开始。

表6-5　镓和二十烷主要热物性对比

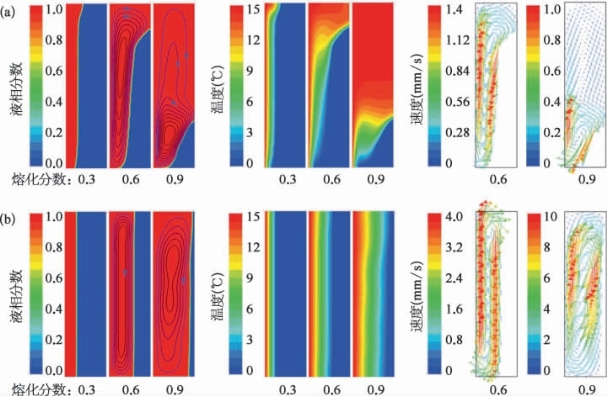
图6-5　熔化过程液相分数云图、温度云图、速度矢量图

（a）二十烷；（b）镓。

图6-5直观展示了两种相变材料熔化过程中的液相分数云图、温度云图和速度矢量图，这里主要选取了熔化分数分别为0.3、0.6和0.9的3个时刻。其中，在液相分数云图中还插入了液相区域自然对流的流线。对于二十烷，固液界面线为倾斜向上，温度分布呈现水平分层，这是典型的自然对流传热的特征。而对于镓，固液界面保持竖直方向向右推进，温度分布呈现竖直分层，这是典型的热传导的特征。从液相速度分布矢量图可以看到，液相镓中的自然对流速度是二十烷的3倍左右，这主要是因为镓的黏度比较小。

尽管液相镓中的自然对流流动比较强，但其传热过程是热传导主导型的，也就是说自然对流传热可以忽略。在液相二十烷中，尽管自然对流流动相对微弱，但是由此带来的传热强化相对于其热传导而言是不可忽略的，甚至是最主要的。造成这一差异的主要原因在于两种相变材料热导率之间巨大的差异。从表6-5可以看到，镓的热导率是二十烷的225倍。高的热导率赋予了镓良好的导热性能，而二十烷低的热导率则严重阻碍了其内部的热量传递，需要依靠自然对流过程来强化其传热储热过程。

图6-6定量对比了镓和二十烷的熔化过程，包括熔化分数、从壁面流入相变材料的热流量以及相应的无量纲换热系数等参数随时间的变化关系。这里分别给出了高温边界的相对温度（TH-Tm）为5℃、15℃和25℃的情形。在熔化开始，存在一个很大的热流，随后在贴壁面处形成熔化液膜。液膜的存在实际上充当了壁面和固相之间的一个传热热阻，因此，随着时间的推移，液膜越来越厚，热阻越来越大，相应的热流密度不断降低，熔化分数曲线的增长速率也逐渐下降。

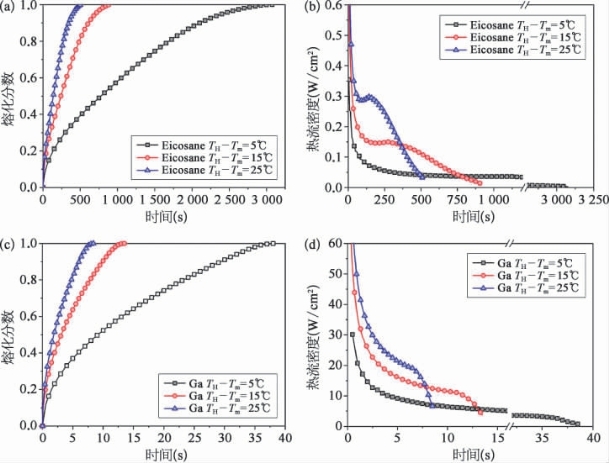
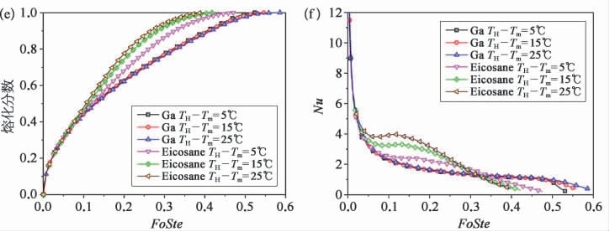
图6-6　镓与二十烷（Eicosane）熔化过程对比

（a）十二烷熔化分数；（b）十二烷热流量随时间的变化；（c）镓熔化分数；（d）镓热流量随时间的变化；（e）镓和十二烷的熔化分数；（f）镓和十二烷的Nu数随无量纲时间Fo·Ste的变化。

随着液相区域的不断扩大，其内部的自然对流也逐渐发展起来。在某一临界时刻，当液相区域的温度不均匀性带来的浮升力足以克服其环流阻力时，自然对流随即形成。从图6-6（b）可以看到，对于二十烷，其热流会在某一时刻突然升高，这也就是自然对流形成的时刻。自然对流强化了其液相区域内的热量传递，因此有效增加了其储热速率。而对于镓而言，其热流一直保持下降趋势，自然对流的形成并未明显影响其储热速率，这与前面图6-5中得到的结论是一致的。

从图6-6也可以看到，对于二十烷，在边界相对温度分别为5℃、15℃和25℃时，其完全熔化所需时间分别为3 080 s、515 s和910 s。而对于镓而言，完全熔化所需时间则大大减小，分别为38 s、13.5 s和8.5 s，大概是前者的1／100。对比两者的体积相变潜热可以发现，镓的体积潜热为489 mJ／m3，二十烷的为194 mJ／m3。也就是说，在同等体积下，熔化镓所需的潜热量是二十烷的2.5倍。从储热热流量来看，二十烷在熔化中的热流量基本保持在10-1W／cm2量级，而镓则高达101W／cm2，比前者高出两个数量级。从这一系列定量的对比可以看到，就热性能而言，低熔点金属的相变吸热性能远高于传统的石蜡类材料。

为更清晰地认识两类相变材料相变传热过程的本质差别，这里给出无量纲分析。一般常用Fo数来表征无量纲时间，而对于固液相变问题而言，考虑到相变过程的影响，常用Fo数与Ste数的乘积来表征无量纲时间，也就是：

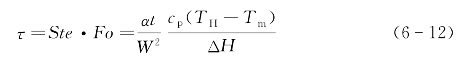
其中，W是竖直腔体的水平宽度，这里作为这一问题的特征长度。

熔化分数φ和换热强度Nu是熔化过程中最关心的两个主要无量纲参数。熔化分数是指相变材料的熔化体积的百分比，可以用下式计算得到：

Nu数可用下式计算得到：

(www.xing528.com)

其中，q″（t）为从恒温壁面流入相变材料的实时热流密度。

图6-6（e～f）展示了这两种相变材料的熔化分数和Nu数随无量纲时间τ的变化规律。可以看到，对于镓，在这3种参数条件下，其无量纲曲线几乎是完全重合的。而对于二十烷，在不同的加热条件下其熔化过程曲线不一样，边界壁面温度越高，其Nu数越大，相应的熔化速度越快，总熔化时间越短。造成这种差异的本质原因实际上是自然对流的影响。Ra数是表征自然对流换热强度的无量纲数，其定义如下：

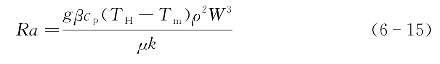
从物理意义上来讲，它也可以理解为是对流换热与热传导的比值（再乘以一定的比例因子）。当Ra数小于某一临界值时，热传导占主导地位；当Ra数较大时，对流换热开始起作用甚至占据主导地位。对于这里研究的问题，当壁面相对温度为15℃时，镓的Ra数为552，远小于二十烷的45 659。这也解释了为什么在无量纲尺度下，镓的熔化曲线基本重合，而二十烷的会有所变化。这是因为，对于镓而言，这里研究的几种情况下的Ra较小，自然对流不会影响其传热过程。而对于二十烷，Ra较大，自然对流传热也相对较强，因而熔化过程也得到加速。

可以看到，由于热物性上的巨大差异，低熔点金属相变材料与传统有机相变材料的相变传热过程实际上存在很大差异。为进一步弄清楚其相变传热的一般规律，下面给出参数化的数值计算结果，分别针对恒定壁温和恒定热流两种情况进行分析。

6.4.2.3　恒定壁温边界条件熔化过程

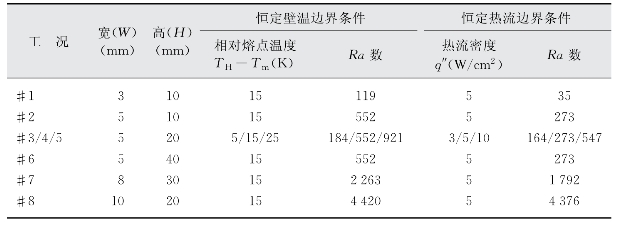
这里，针对在实际热控应用中可能遇到的几种尺寸和温度情形进行数值计算，具体参数列于表6-6。图6-7展示了8种不同情况下的熔化过程。在图中图例部分，HaWb表示腔体的高度（H）和宽度（W）分别为a mm和b mm；5 K表示给定壁面温度为熔点以上5℃。

表6-6　腔体内相变过程模拟工况参数列表

对比＃2、4、6可以发现，三者的熔化过程曲线是完全重合的，也就表明在该条件下，腔体高度对熔化过程没有明显影响。＃3、4、5之间唯一的不同是壁面温度大小，不难理解，温度越高，熔化过程越快。对于壁面温度相同的几组，如＃1、2、4、6—8，其热流密度大小与时间的关系遵循同一条变化规律曲线。

通过无量纲化，可以很容易发现其中的规律。图6-7（b）和（d）是熔化分数和Nu数随无量纲时间FoSte的变化曲线。可以看到，在无量纲尺度下，镓的熔化过程表现出很好的规律性，研究的几种情形的结果完全重合。通过拟合，可以给出如下表征恒壁温下低熔点金属熔化过程一般规律的无量纲关系式：

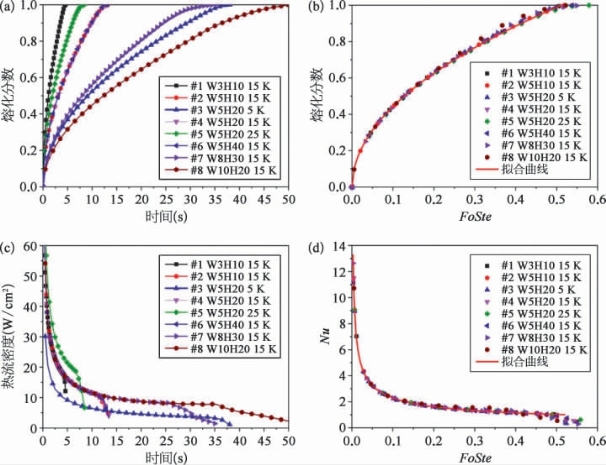
图6-7　不同壁温和不同腔体尺寸下镓的熔化过程曲线

（a）熔化分数随时间的变化；（b）熔化分数随无量纲时间FoSte的变化；（c）热流密度随时间的变化；（d）Nu随FoSte的变化。

6.4.2.4　恒定热流边界条件熔化过程

类似地，这里也给出了恒定热流边界条件下的情形，相应的参数列于表6-6。在恒热流边界条件下，部分无量纲参数的定义中涉及特征温度（ΔTc=TH-Tm）的部分需要做一定的修改，因为此时壁面温度TH是未知的随时间变化的量。可以用已知的边界热流密度q″来重新定义特征温度：ΔTc=q″W／k。基于这一定义，其他的无量纲变量可以重新定义为：

图6-8总结了针对8种不同情形的计算结果，可以看到，熔化分数随时间几乎线性增加。此外，壁面温度也会随时间线性增加，并在最终熔化快要结束时急剧上升。通过对无量纲曲线进行拟合可以给出如下关系式：

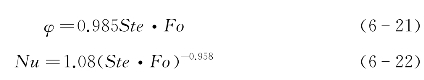
至此，已经得到了表征恒壁温和恒热流下低熔点金属熔化过程一般规律的无量纲关系式。而对恒定壁温边界条件，其一维斯蒂芬问题有如下精确解［11］：

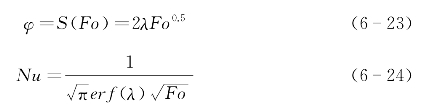
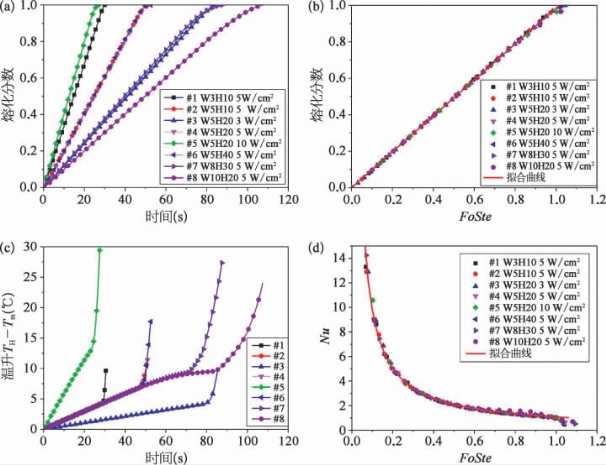
图6-8　不同边界热流密度下镓的熔化过程曲线

（a）熔化分数随时间的变化；（b）熔化分数随无量纲时间FoSte的变化；（c）壁面温度随时间的变化；（d）Nu随FoSte的变化。

在小Ste数（Ste＜0.2）下，有如下近似［11］：

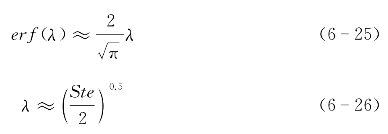
于是，熔化分数和Nu数可以近似表达为：

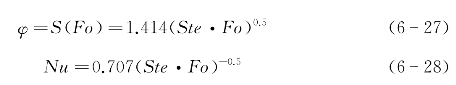
可以看到，这与式（6-16）和式（6-17）非常接近，也就是说，低熔点金属的对流型固液相变传热问题与不考虑对流的传导型相变问题的结果是一样的，这说明其中的自然对流传热实际上是可以忽略的。

同样，针对恒热流情形，杨小虎等［11］给出了一种近似解：

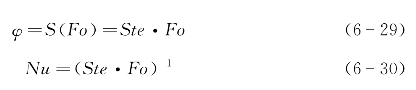
这里得到的式（6-21）和式（6-22）也十分相近。两者的差别在于，在近似解中，忽略了显热吸热的影响，因此式（6-29）中的常数系数比式（6-21）略大一点。

这里所分析问题的Ra数均较小，因此热传导占据主要地位。从表6-6可以看到，针对恒壁温和恒热流，这里研究的Ra数的最大值分别为4 420和4 376，且在这一Ra数时，相应的无量纲曲线已经开始小幅度地偏离拟合曲线。因此可以认为，对于低熔点金属，Ra数小于4 000时，可以忽略其自然对流的影响，只考虑其热传导过程即可。