测量热导率的方法简介

热导率和热扩散率都是表征材料热传递性能的物性参数，准确获得材料的热物性参数对各种材料的应用均非常重要。目前，热导率主要依靠实验测量的方法得到，相关方法有很多种，但是各自的测量条件、测量参数的个数、测量精度和试样尺寸都不尽相同［11］。

热导率测量方法一般可以分为稳态法和非稳态法两大类，稳态法指的是实验中待被测试样上的温度分布达到稳定后再进行测量，其数据分析的依据是稳态的导热微分方程，能直接测得热导率，特点是实验公式简单，但实验时间长，需要测量导热量（直接或间接）和若干点的温度。非稳态法指的是实验测量过程中被测试样的温度随时间变化，其分析的依据是非稳态导热微分方程。测量原理是对处于热平衡状态的试样施加某种热干扰，同时测量试样对热干扰的响应（温度随时间的变化等），然后根据响应曲线确定试样材料热物性参数的数值。在非稳态测量方法中，测量信号是时间的函数，因而可以分别或同时得出热导率、体积热容，以及组合参数如热扩散率、蓄热系数等。

由于稳态法一般耗时较长，因此非稳态热导率测试技术近年来成为研究热点，而瞬态平面热源技术则是众多非稳态法中应用相对比较多的方法［11］。其中常用的非稳态测量方法包括热线法、热探针法、热带法和平面热源法等。

2.3.1.1　热线法

热线法可用来测量固体、粉末和液体的热导率，温度范围从室温到1 800 K，能够同时得到比热和热扩散率，但准确性较差。它有3种基本测试形式［11］：交叉热线、平行热线和热电阻式热线法。交叉热线法适用的热导率区间在0.05～5 W／（m·K），平行热线法最高可测至25 W／（m·K）甚至更高。另外，热线法既可用于各向同性材料，也可用于各向异性材料，材料可以是均质的，也可以是非均质。热线法的原理如图2-4和图2-5所示，将一根均匀细长的金属丝（线）埋设在待测试样的凹槽内或者紧密夹持在两块试样中，当有电流通过时，细丝内就有热量产生，热量沿径向在试样中传导。测量并记录细丝的温度响应（温升随时间的变化）或距细丝某个距离处的温度响应，然后根据细丝—试样实验系统的传热数学模型及温度变化的理论公式，就可计算出被测试样的热物性参数。在交叉热线和平行热线法中，温度响应通过焊接在热线上的热电偶或布置在试样内的热电偶测量得到。而在热电阻式热线法中，热线本身既是加热元件也是测温元件，温度响应是通过测量热线本身的电阻变化来获得的，不需要设置另外的热电偶。最常用的热线材质是纯铂，其他已知电阻温度系数的性能稳定的电热金属也可以，热线典型的长度为100～200 mm，直径为25～500μm，测量液体时其直径可小到5μm。

图2-4　交叉热线法示意［11］

图2-5　平行热线法示意［11］

热线法温度响应的理论公式如下：

式中：ΔT（r，t），温升，即温度与系统初始平衡温度之差（T-T0）；r，半径；t，时间；λ和a，试样的热导率和热扩散率；Ei，指数积分函数；q，热线上每单位长度的发热量。

当加热一定时间之后，即满足条件：时，可得到简化的公式：

式中：欧拉常数（0.577 2）。

对于热电阻式的热线法，温度响应通过测量热线上电压的变化来获得：

式中：a，热线的电阻温度系数；r0，热线的半径。

如果画出温升ΔT（r，t）随对数时间ln t的变化曲线。曲线呈线性变化趋势，直线的斜率m=q／（4πλ），截距n=m ln p［4a／（C*Er2）］，据此可以得到被测试样的热导率λ和热扩散率a：

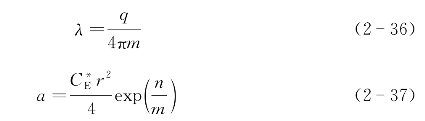
由式（2-37）可见，热扩散率a的测量误差较大，因为理论上要求热线要非常细，即r→0，而半径r的数值太小会导致无法获得很准确的热扩散率值。所以，如果采用交叉热线法的话，一般只能测得热导率。热导率λ的测量精度取决于温度T和发热量q的测量精度，一般测量误差可以控制在3%左右甚至更小。

2.3.1.2　热探针法

热探针法的原理也是基于热线法［11］，只不过用探针取代了热线，可以测量各种均质固体和粉末状材料的热导率和比热，也可以测量非均质的多孔材料，可测量的温度范围为-50～500℃，热导率测量区间为0.05～20 W／（m·K）。热探针法对于测量一些熔融材料、粉末或者含湿材料特别适合，还可以进行现场和野外作业。实验室用的热探针长度通常为200 mm，直径为1～2 mm。

热探针法原理如图2-6所示，折叠的或者螺旋形的细金属加热丝，以及测温元件被封装在一根细长的薄壁金属管内，互相之间要保持绝缘。在一定时间里对探针加热，同时测量并记录探针的温度响应，然后根据探针—试样实验系统的传热数学模型及温度变化的理论公式，就可计算出被测试样的热物性参数。

热探针法温度响应的理论公式或模型有两种，一种为理想线热源模型，与热线法模型相同：

图2-6　热探针法示意

式中：A=q／（4πλ），B=［q／（4πλ）］·［ln（4a／r2）-CE］。

另一种是较为精确的Jaeger修正模型：

式中：A=q／（4πλ），B=［q／（4πλ）］·｛ln［4a／］+4πλ（Γ+W）｝，D=［（qcr2）／（8πλ2）］·｛（1-cp／c）ln［4a／］｝+1-［4πλcp（Γ+W）／c］，E=［（qcr2）／（8πλ2）］·（1-cp／c）。其中：φd，探针的外直径；Γ、W，探针与试样之间的接触热阻以及探针的内部热阻；cp、c，分别为探针和试样的体积热容，其他符号与热线法相同。

若采用理想线热源模型，热导率λ的测量误差与被测材料的结构有关，对于含湿的细颗粒材料误差约为5%，而对于干燥的粗颗粒材料误差有可能超过10%。若采用较为精确的Jaeger修正模型，热导率λ的测量误差为3%～5%，体积热容c的误差比较大，约为20%。在现场或野外作业时，测量误差通常最小也会达到10%。(www.xing528.com)

2.3.1.3　热带法

图2-7　热带法示意

热带法测量原理类似于热线法，不同之处是用很薄的窄金属带（热带）替代热线［11］，如图2-7所示。实验中将薄金属带夹持在待测材料中间，从某时刻起以恒定电功率加热金属带，测量并记录热带的温度响应曲线，根据温度变化的理论公式可同时得到被测材料的热导率和热扩散率。热带法不仅可以测量液体、松散材料、多孔介质及非金属固体材料的热导率，在热带表面覆着一层很薄的绝缘层之后，还可用于测量金属材料，适用范围较广，而且实验装置易于实现。与圆柱状电加热体相比，薄带状电加热体与被测固体材料有更好的接触状态，故热带法比热线法更适宜于测量固体材料，而且热扩散率的测量结果也较热线法精确。另外，热带比细的热线要更加结实耐用一些。热带的温度变化可以通过测量热带电阻的变化来获得，也可以借助在热带表面上焊接热电偶来直接测量获得。

最常用的热带材质是纯铂，也可以使用其他已知电阻温度系数的性能稳定的金属，热带典型的长度为100～200 mm，宽度为3～5 mm，厚度为10μm或更小。

热带法温度响应的理论公式或模型如下：

式中：wh，热带宽度；erf（z），误差函数；q，热带每单位长度的加热热流。

当加热一定时间，即时，可得简化公式：

对于热电阻式的热带法，温度响应是通过测量热带上的电压变化来获得：

如果画出温升ΔT（t）或电压ΔU（t）随对数时间的变化曲线，曲线呈线性变化趋势，直线的斜率为m=q／（4πλ），截距为据此可以得到被测试样的热导率λ和热扩散率a：

由式（2-44）可见，用热带法得到的热扩散率的测量误差比热线法要小得多，因为wh的数值（1～10 mm）比热线的半径大得多，可保证热扩散率值达到满意的精度。热导率的测量误差一般在3%，热扩散率a的测量误差可以控制在4%左右。

2.3.1.4　平面热源法

平面热源法可以快速测量试样的导热系数和热扩散率［11］，其原理是向电热合金制成的金属片通以某种固定形式（阶跃式或脉冲式）的电流，金属片释放热量而成为热源，即平面热源，如下以阶跃式电流为例。使用该热源加热试样，并测量出试样某点（实验中通常取试样某截面的中心点，该点相当于中心探测区）过余温度—时间曲线，根据相应的数学模型和改进高斯-牛顿参数估计法，可以同时测得试样的导热系数λ和热扩散率a，进一步得到体积热容ρc=λ／a，式中ρ表示试样的密度，c表示试样的比热容，其物理模型如图2-8所示。

图2-8　平面热源法示意

对于固体而言，实际的热传导过程都是复杂的三维过程。为了简化分析，假设模型与周围环境之间不存在换热，热量只沿某个固定的方向进行传导，例如厚度方向，这样的模型即是理想一维模型。实际测量中，只要满足半无限大理论模型即可将它认为是理想一维模型，平面热源法正是基于该理论来测量材料的导热系数，相应导热微分方程、初始条件和边界条件如下：

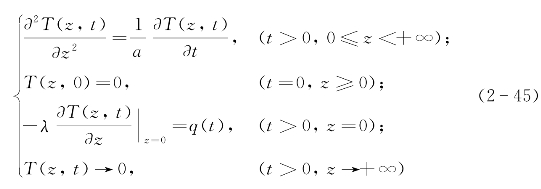
式中：T（z，t）为过余温度，试样真实温度与系统初始温度T0之差，℃；z为热传导方向的空间坐标，m；t为时间，s；λ为试样导热系数，W／（m·K）；a为试样热扩散率，m2／s；q（t）为试样加热面上的热流密度，W／m2，若电流以阶跃形式出现，当加热电流为I，加热片两端的电压为U，平面热源电阻为R，q（t）=Q／（2S）=UI／（2S）=I2R／（2S），Q为加热功率，W；S为平面热源的面积，m2。

对式（2-45）中的时间变量t作完全的拉普拉斯变换（即对偏微分方程和边界条件都作拉氏变换），以求解0≤z＜+∞区间内各截面中心点过余温度随时间的变化关系T—t曲线，设象函数为θ（z，p），变换后得到：

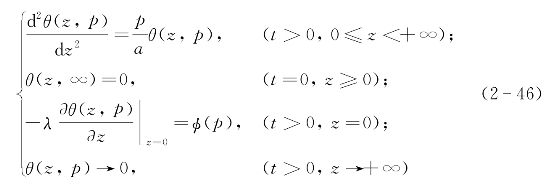
式中，p为拉普拉斯变量，θ为温度T（z，t）的拉普拉斯变换，为热流q（t）的拉普拉斯变换，其中：

求解式（2-46）得到：

以阶跃式电流通过金属片，加热时间内，q（t）为常数，利用拉氏反变换对式（2-49）进行求解，得到相应的数学模型：

式中，erfc为余误差函数。

在式（2-50）中被测试样厚度z=z0处的平面中心点处，过余温度T（z0，t）随时间t的变化是实验中可以使用多通道数字示波器直接测量得到的，因此式中仅含导热系数λ和热扩散率a两个未知参数。又由于λ和a是线性无关的，根据式（2-50），可以利用改进高斯—牛顿参数估计法编写程序同时计算出λ和a这两个参数，进一步可以得到体积热容ρc=λ／a。

加热过程中，金属片两端的电压U和电流I也都可以使用多通道数字示波器测量得到，金属片的有效加热面积S可以直接测量得到，因此q（t）=UI／（2S），为常数。