预测液态合金的热导率

液态金属的热导率可表示为

其中，λL表示声子对合金热导率的贡献，而λe表示电子对合金热导率的贡献。对许多金属或者合金来说，电子对热导率的贡献依旧处于支配地位，因此我们忽略了声子对热导率的贡献，即假设λ=λe，根据威德曼-弗朗兹-洛伦兹（Wiedemann-Franz-Lorenz，WFL）定律［4］，可得

式中，α为Seebeck系数。对非半导体材料而言，同相比，α2的值比较小，因而可以忽略。即对大多数金属而言，

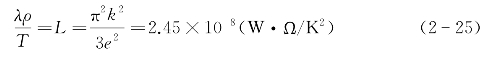
从定量上看，这种关系是基于这样一个事实：在液态金属或合金中，热量传递和电子传递均与自由电子密切相关。热导率随电子平均运动速度的增加而增加，因为电子直接进行了能量传输。而电导率却减少，因为粒子间相互碰撞改变了电子运动的方向。热导率和电导率的这种相关性表明，在金属中，自由电子既充当导电的载体，又充当导热的载体。20世纪50年代，苏联物理学家朗道提出了“费米液体”理论，把金属中大量的电子视作“费米液体”，从微观角度解释了自由电子的这种行为［5］。学术界研究发现［6，7］，WFL定律对汞铟合金也适用，根据文献数据［8］，WFL定律还可用于Bi0.85Sb0.15合金。由于电阻率测试比热导率测试容易得多，因此根据电阻率来预测热导率是一个可行的方法。

但是，也应注意到，实际测量中，洛伦兹数并不一定是一个常数，而且有时与温度相关（当然也可能测量时存在误差）。比如，钠的洛伦兹常数可以表示为［1］

钾的洛伦兹常数为

从方程（2-14）和（2-24），可得到二元合金的热导率为

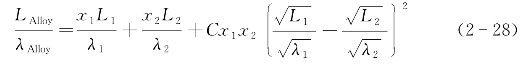(www.xing528.com)

对大多数金属而言

式（2-28）简化为

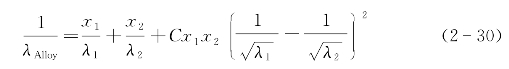
值得注意的是，式（2-26）到（2-28）中的洛伦兹数是计算出来的宏观数据，即在（2-24）中代入电阻率的值和热导率的值，众所周知，金属的电阻率和热导率测量都会带来较大误差，因而，宏观洛伦兹数对计算合金的热导率不一定合适，除半导体之外，我们还是取洛伦兹数为常数，即假设式（2-25）对所有金属都成立。

由式（2-21）和（2-24），可得熔点时固态热导率和液态热导率的关系：

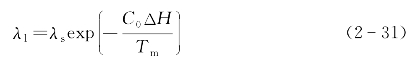
式中，λl和λs分别为液态和固态下的纯金属热导率。比如，要计算50℃的液态镓铟合金热导率，纯镓在50℃时为液态，而金属铟在此温度下为固态，因此需要把铟的热导率数据转化为50℃下的液态热导率值，尽管金属铟在50℃下很可能不存在液态。而ΔH为潜热，单位为kJ／mol，C0值可取为80［9，10］。

对于可能由于测试带来洛伦兹数产生误差的问题，研究者设计了一种仪器来测量液态金属的洛伦兹数，温度可高达773 K且具有很高的精度［6］。前人测试发现，液态镓、汞和锡均与WFL定律符合很好。对多价金属二元合金，Zm≥3，合金热导率可以简化为

值得注意的是，采用式（2-31）预测的二元合金的热导率与浓度并不呈线性关系，为直观起见，假设液态金属A与B的导热系数分别为20 W／（m·K）、40 W／（m·K），则其线性插值和按照式（2-31）的区别如图2-3所示。

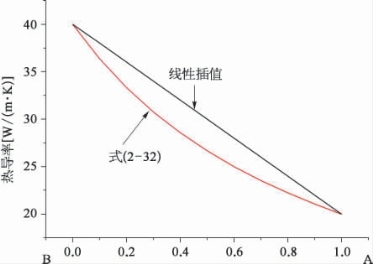
图2-3　合金热导率的线性插值与式（2-32）计算比较