液态金属的电阻率特性分析

金属及合金的热导率与电导率的比值为常数，一般可以由电导率对热导率进行预测［2］。由Faber-Ziman公式［3］，液态合金的电阻率可写为

其中，为普朗克常数与2π之比；|e|为电子电荷；vF为费米速度。对一质量为m的电子而言，有

wα（q）和wβ（q）为价电子α和β的库仑势的傅立叶变换。xα和xβ分别为摩尔分数。

在式（2-1）中

这里，kF为波矢，Z为合金有效化合价，对价电子数为Zα和Zβ的二元合金来说，合金有效化合价可表示为

在式（2-1）中，为简单起见，采用Faber和Ziman提出的置换模型，在这种置换模型中，所有组分都具有相同的原子体积和结构因子，即

长波长PY硬球结构因子表达式为

其中

其中，m=σq，σ为金属的硬球半径。式（2-7）为结构因子的唯一的理论关系式，因而在液态金属理论中得到广泛应用。根据Faber和Ziman理论［3］，液态金属的表达式可分解为

其中

从式（2-9）～（2-11）可以看出，液态合金的电阻率中ρ′与浓度呈线性关系，而ρ″则与浓度呈二次方关系。

对于二元合金，xα=1和xβ=0对应电阻率ρ1为纯液态金属，而xα=0和xβ=1对应电阻率ρ2为纯液态金属β，也即，

从式（2-9）～（2-13），不考虑相变，我们得到二元合金的电阻率表达式(www.xing528.com)

其中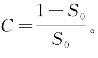，S0为S（q）从区间0到2kF的平均值。我们知道，对单价金属，在整个区间内，结构因子S（q）远远小于1，可用S（0）代替。图2-1为区间上限2kF在硬球结构因子S（q）上的位置示意图。

图2-1　结构因子SH（q）曲线上不同化合价的2kF位置示意

而S0的表达式可由下式得出

其中，

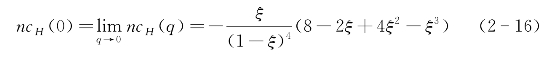
将方程（2-16）代入（2-15）可得其中，ξα和ξβ为液态纯金属α和β的堆垛分数，

其中，n为单位体积粒子数。对碱金属来说，ξ介于0.47和0.8之间，因此，对两种一价金属，比如钠、钾、金、银来说，由于C＞0，合金的电阻率ρAlloy与x的关系曲线往上凸起。合金的电阻率可由式（2-14）～（2-19）计算。而对于多价金属，S（q）在q的范围内接近或大于1，式（2-1）中的积分完全由〈…〉Z决定。对多价金属铝、铟、锡，常数C的值几乎为零，因此，合金电阻率与浓度几乎呈线性关系。所以，对多价金属合金（Zm≥3），电阻率可简化为

如果发生相变，即使在相同温度下电阻率也将发生变化。Mott［4］提出了一个公式计算熔点温度时液态电阻率与固态电阻率之比，即

其中，ΔHTm为熔化焓或熔化潜热，单位为kJ／mol。

假设固态金属α，电阻率为ρ1，与另一种电阻率为ρ2的液态金属形成合金，则金属α的虚拟电阻率可表示为

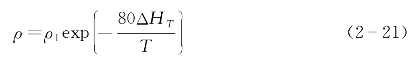
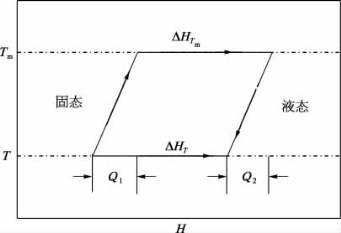
图2-2　固态到液态转变过程

为简化起见，可以假设Q1=Q2，因此，

即在式（2-21）中，ΔHT可用熔点温度时的潜热代替。