基于触发器级的时序逻辑电路设计优化方案

时序逻辑电路的一般设计方法是一种基于触发器级的状态化简法，其具体设计步骤如下：

（1）将实际问题抽象为逻辑问题，根据问题的因果关系作状态表或者状态转换图。

（2）状态化简。

（3）确定触发器的数目、类型及状态编码，作状态转换的卡诺图。

（4）求状态方程、驱动方程和输出方程。

（5）根据得到的方程式作电路图。

（6）检查设计的电路能否自启动。

【例4.4.1】 试设计三相六拍制的步进电机控制器。

【说明】步进电机是将电脉冲信号转换成角位移的一种机电转换器。它具有快速启停、精确步进的特点，被广泛用于需精确定位的位置控制系统中。例如，打印机打印头的移动、磁头沿磁盘半径方向的进动以及机器人四肢动作等都是依靠步进电机。步进电机的角位移与输入脉冲的个数成正比，其转速与输入脉冲的频率成正比，其转动方向由输入脉冲对电机绕组的加电顺序决定。正向转动的通电顺序为A→AB→B→BC→C→CA→A，反向转动的通电顺序为A→AC→C→CB→B→BA→A。

解：（1）将步进电机的每一拍通电看作一个状态，得到状态转换图S0→S1→S2→S3→S4→S5→S0。

（2）对于步进电机来说，S0～S5的任何一个状态都不能省略，否则会导致步进电机失步。所以S0～S5为最简状态。

（3）选取三个D触发器，每个触发器输出的高电平使步进电机的一相绕组通电，步进电机电路如图4.4.1所示。对S0～S5六个状态进行编码并得编码后的状态转换图，如图4.4.2所示。

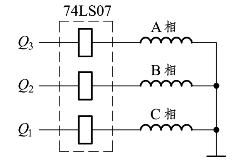
图4.4.1　例4.4.1的步进电机电路

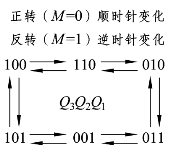
图4.4.2　例4.4.1的状态转换图

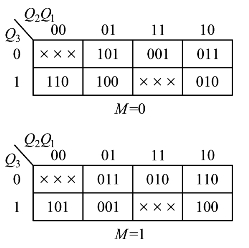
图4.4.3　例4.4.1的卡诺图

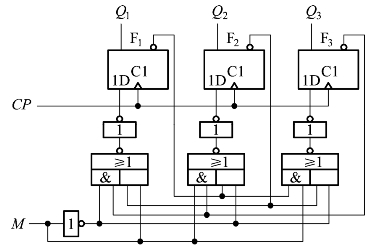
图4.4.4　例4.4.1的步进电机驱动电路图

（4）选取M为正反转控制信号，当M＝0时步进电机正向转动，当M＝1时步进电机反向转动。由图4.4.2得Q3Q2Q1的卡诺图，如图4.4.3所示，这里的一个卡诺图相当于三个函数的卡诺图的重叠。注意前一个状态与其后一个状态的关系是初态与次态的关系。在上卡诺图中，当初态Q3Q2Q1＝100（坐标值），其次态Q3Q2Q1＝110（见卡诺图4.4.3的左下角）；当初态Q3Q2Q1＝110（坐标值），其次态Q3Q2Q1＝010（见卡诺图4.4.3的右下角）；当初态为Q3Q2Q1＝000或Q3Q2Q1＝111时，其次态为约束项×××。

根据Q3Q2Q1的卡诺图可得状态方程和驱动方程：

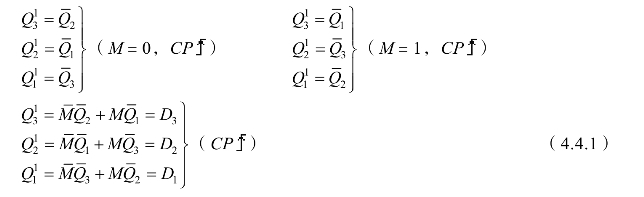(www.xing528.com)

（5）根据驱动方程式（4.4.1）作步进电机控制器的电路图，如图4.4.4所示。

（6）该时序逻辑电路有一个无效循环：，应避免电路进入这个循环。

【例4.4.2】试用基于触发器级的方法设计8位串行数据序列检测器，被检测数据序列为10110010。若检测到该序列则检测标志F置1，否则为0。

解：（1）定义状态，并列出状态表，如表4.4.1所示：设串行数据输入变量为A，数据从高位开始输入。用Si表示依次输入了i位有效数据后电路的状态，即S0（0），S1（1），S2（10），S3（101），S4（1011），S5（10110），S6（101100），S7（1011001），S8（10110010）。

（2）状态化简：从表4.4.1可以看出S8和S0两个状态是等价的，所以实质上只有8个有效状态。将S8用S0代替。

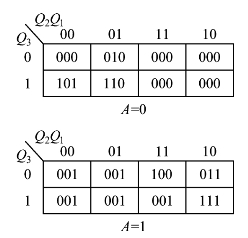
图4.4.5　例4.4.2的卡诺图

表4.4.1　例4.4.2的状态表

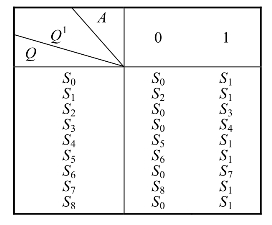
（3）因为只有8个有效状态，所以选取三个JK触发器。对下列8个状态编码：S0→000，S1→001，S2→010，S3→011，S4→100，S5→101，S6→110，S7→111。根据表4.4.1和状态的编码作用这三个JK触发器的次态Q3Q2Q1的卡诺图，如图4.4.5所示。

（4）根据Q3Q2Q1的卡诺图可得状态方程、驱动方程和输出方程为

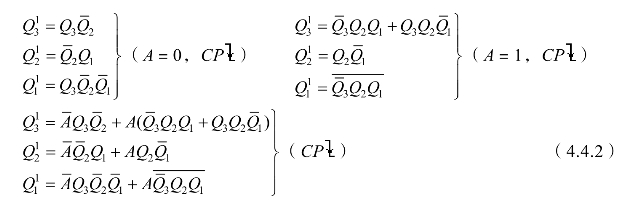
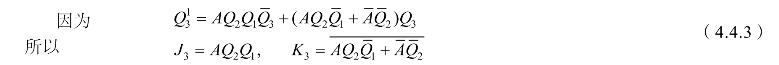
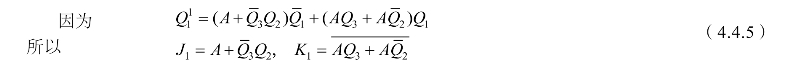
当电路的状态为S7（1011001），即Q3Q2Q1＝111时，若此时A＝0则检测标志F＝1，否则F＝0。由此得输出方程为

（5）根据式（4.4.3）～式（4.4.6）作8位串行数据序列检测器的电路图，如图 4.4.6所示。

（6）因为该电路中只有三个触发器，含8个有效状态，所以该电路没有无效状态。

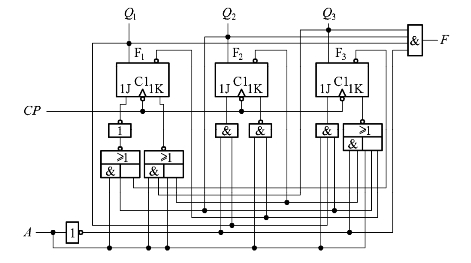
图4.4.6　例4.4.2的电路图

【说明】与例4.2.3相比较，基于触发器级的时序逻辑电路设计能够做到电路最简。本例只用了三个触发器，而例4.2.3用了八个触发器。但例4.2.3的设计思路简单，像搭积木一样，设计效率高。