冲刷率与冲刷量的关系分析

冲刷率有两种概念：一种是由Laursen于1952年提出的，冲刷率等于出冲刷区的输沙率与入冲刷区的输沙率之差；另一种是用单位时间，单位床面被水流冲离床面并被水流带走的泥沙量来表示。后一种概念采用较多。

1.Partheniades冲刷率公式

假定床面瞬时切应力τ0服从正态分布，时均值为标准差，又假设cf为颗粒间的吸附力，c为包括cf在内的土壤黏着力，σmax为水流作用在粒间触点或在黏粒内形成的张应力，直接与τ0有关，由此得到一个冲刷临界表达式

式中：K为比例常数。引入τ0服从正态分布等若干假设，最后得到冲刷率表达式为

式中：E为冲刷率；Ds为平均粒径；γs为颗粒比重；A为无量纲形状系数；w为积分变量；t（τ0）为移动一个黏粒或絮团需要σmax≥cf作用的时间。

此式把水流参数和土壤性质分成两个因子，ADsγs/t（τ0）是土壤性质的函数，τ0η0决定于床面形状和水流条件。其适用范围是：水流切应力小于床面抗剪强度，但大于床面颗粒的最大黏结力。原作者认为此式仍是定性的表达式，因为待定常数众多，实用还有一定困难。

上式方括号内的部分，实质是冲刷力大于抗冲力的概率，最多只能等于1，所以冲刷率的最大极限为

实际计算结果，当切应力较大时，冲刷率很快可接近极限值，这时当切应力再增加时，冲刷率几乎不再增加。究其原因主要是公式中引入的时间t（τ0）与水流条件无关造成的。我们可以从量纲分析来重新描述t（τ0），就可以改善这一困难。

t（τ0）的物理意义是指当水流切应力满足冲刷条件后，掀走一个颗粒所需要的作用时间，这应与水流条件U*，水流黏性γ和粒径有关，即存在关系

可表示成d/tU*=F（U*d/γ），进一步设F（U*d/γ）=βU*d/γ。

则得到，于是冲刷率公式可化为

分别用Partheniades公式和式（1）验证Patheniades实验可看出式（1）克服了上述困难（见图2）。

图2　冲刷率公式比较

2.Ariathurai冲刷率公式

Ariathurai由试验得出冲刷率经验公式

式中：为时均床面切应力；τc为临界切应力；M为抗冲系数。

M与颗粒的阳离子交换量、钠吸收比、水的离子含量的关系公式形式简单，生产使用可能比较方便。但是，由于M建立的关系众多，计算时由不同参数得到M值很难一致。

3.Abdel-Rahmann冲刷深度公式

Abdel-Rahmann从水槽试验分析出的冲刷深度公式：

式中：h为冲刷深度；R为水力半径；J为能坡；P和b为决定于黏土矿物性质和水流黏度常数；S为抗剪强度。(www.xing528.com)

这也是一个经验公式。

4.用“速率论”方法分析黏性土冲刷的三个冲刷率公式

“速率论”是一种分析工具，具有广泛的用途。其理论建立在统计力学基础上，最先用于物理化学领域，随后在流变学、水泥、陶瓷、金属、沥青和黏土的蠕变研究中得到广泛应用。

（1）Raudkivi和Hutchison发现试验中冲刷率随水温变化。这个现象可以用类似土力学中黏性土蠕变的速率论公式来描述。根据试验资料，拟合两组试验的冲刷率公式为

式中：Ea，Eb分别为两组试验的冲刷率；R为通用气体常数1.98cal/（K·mol）；T为绝对温度，K。

作者并未提出冲刷机理的解释，只是由冲刷率与温度有关的现象作了推测，尽管还比较粗糙，但这是第一次把速率论与黏性土冲刷联系起来了。

（2）Christensen和Das的小管路试验表明，冲刷率与切应力和温度关系与速率论一致，他们得到的试验活化能和试验流动体积较黏性土蠕变的结果低。从蠕变移植的冲刷率公式为

其中

式中：X为一个函数，决定于τ0作用方向流动单元的数量和克服一个能垒在此方向的移动分量；K为波尔兹曼常数1.38×10-16尔格/°K；h为普朗克常数6.624×10-27尔格/秒；ΔE为越过能垒的自由活化能；λ为颗粒相邻两平衡位置的距离；S为单位面积上流动单元的数量。

上式中确定S、λ和X比较困难，作者取对数后对1/T微分得到

式中：N为阿佛加得罗常数，6.02×1023（N=R/K）。作者最后分析就用此式，通过建立ln（E/T）和1/T的关系，其斜率就是试验活化能ΔE-λNτ0/2S的值。切应力与冲刷率的关系规律也较好（见图3）。求出一个重要的活化参数一试验活比能，对高岭土，=16.3kcal/mol，对Grundite泥，=15.4kcal/mol。此外还用实验数据分别算出了a，β和S的值。

图3　水流切应力与冲刷率关系

（3）Gularte在《黏性土抗冲性》博士论文中，直接移植了两个蠕变的速率论公式：一是Mitchell的试验活化能公式

二是Andersland的试验流动体积公式：

式中：T1，T2为不同测次的温度；E1，E2为对应的冲刷率；τ1，τ2为对应的床面切应力；其余符号同上。

移植中将轴向应变率改为冲刷率，有效切应力换水流切应力。对机理的描述仍旧是不够严密的。作者认为，既然在蠕变时认为越过能垒的流动单元的速率正比于轴向应变率，那么，对于具有定常结构的土壤冲刷，有理由假设在切应力方向越过能垒的流动单元的速率会正比于离开土壤表面的颗粒的速率，即正比于冲刷率。这种演绎的方法有一定道理，但显然不够严密，是否能更严密地对黏性土冲刷的速率论分析作出解释，也是一项有意义的工作。

作者的试验就是按上两式安排的，主要任务就是根据试验数据得出试验活化能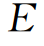和试验流动体积Vf。上两式给出的冲刷率E1、E2都是相对值，计算时除了已知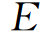和Vf外，还应知道一组基准τ、T作用下的冲刷率，才能算出其余各种τ、T之下的冲刷率E。

作者既肯定了速率论研究黏性土冲刷的潜力，又指出现有研究成果仍属定性研究。