设c为淤积过程的瞬时含沙量（kg/m3）；c1为初始含沙量。试验表明，对应相同的c1，在不同的床面切应力τ作用下，用无尺度含沙量c/c1表示的淤积过程是不同的。图8给出了c1=4.85kg/m3的8组试验的淤积过程。图8中显示，含沙量在经历很短一段时间后就逐步达到一种持续不变的含沙量c2。切应力τ越大，达到稳定浓度的时间越短。τ=7.4N/m2时，10h左右才达到c2。τ=36N/m2时，仅在半小时内即已达到c2。这说明黏性土的淤积过程与床面切应力密切相关。当τ小于一定值时，不再存在稳定浓度c2，经过较长时间以后，全部悬浮泥沙均会淤积。图9给出了一个有趣的结果，对相同的床面切应力τ=16.1N/m2，4种不同初始浓度c1，最后达到的稳定浓度c2仍不相同。c1高的，c2亦高。这一点正是黏性土淤积与非黏性土淤积性质根本不同的地方。后者具有水流挟沙力的概念，即在τ和d相同的条件下，经过足够的时间，无论初始浓度是否相同，最终达到的平衡浓度是相同的。
图8 淤积过程
将c2无尺度化，得到c2/c1。图10绘出了全部试验组次的c2/c1与τ的关系。从图中可以看出，对相同的τ，尽管c1相差10倍，但c2/c1却基本相同。这里c2/c1表征了黏性土的一种的特征，即当τ一定时，c1中不能淤积的那一部分c2所占的比例是一定的，与c1的绝对值基本无关。图10还看出，当τc=6.8N/m2时为一转折点，τ大于τc时存在c2/c1，而τ＜τc时c1会全部淤积，不存在c2，所以τc称临界淤积切应力。将切应力无尺度化，得到c2/c1与（τ/τc—1）的关系如图11，用回归分析得到对数函数的相关关系
图9 c～c1关系
图10 c2/c1—τ关系(www.xing528.com)
从以上分析可知c1—c2表示淤积到稳定状态时用浓度表示的最大淤积量。c1—c表示淤积过程中某时刻以前的淤积浓度。这样用
构成一个无尺度淤积浓度，能直接反映淤积过程。图12给出了无尺度淤积浓度c*与无尺度淤积时间t*=t/t50的关系。t50是一个统计参数，表示淤积过程的均值时间，对应于c*=0.5的历时。由图13可以看出，c*与t*的关系基本上可用Г（t*）分布来描述
图11 c2/c1～（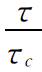
-1）关系
图12 c*～t*关系
式中：Γ（α）为Г函数，记为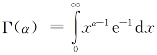
，x为积分变量。Г分布中的统计参数α和β有可能综合反应黏性土淤积时的诸多复杂因素。在我们的试验中，α=0.5，β=0.25。进一步将式（5）两端对时间t求导数，得到淤积率表达式
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
