排沙底洞冲刷空库的效果探析

恢复库容的数量取决于冲刷时河槽的纵横剖面。而特别是纵剖面的发展同冲刷时间密切相关。

（一）冲刷河槽的横剖面

水槽子水库自1978年以来，有多次空库冲刷的观测资料。假定未来的冲刷流量与现在相同，深槽的形状可考虑与目前相同。

水槽子水库的冲刷河槽为窄深河槽，可概化为梯形，其底宽约10m。因断面窄深，边坡系数对库容计算的结果影响较大。图17是历次冲刷后深槽边坡系数m值在水库内的分布概况。m值的计算为

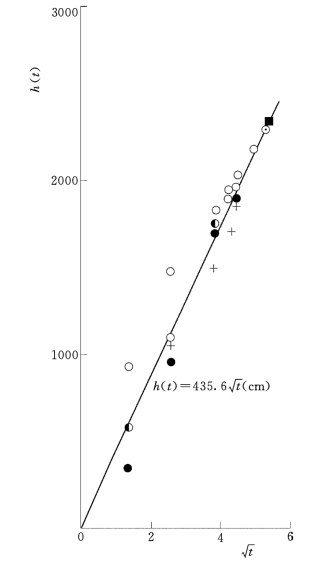
图14　水槽子水库坝前淤积厚度的增长过程

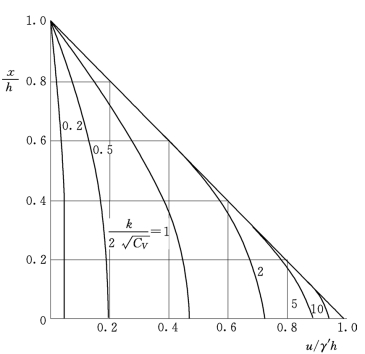
图15　u/γ'h与x/h关系（h=kt1/2）

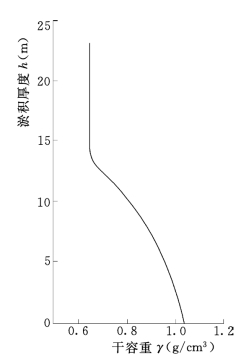
图16　坝前黏性淤积物干容重分布计算结果

式中：m为两岸边坡系数的平均值，ΔZ为高程增量；ΔB为槽宽增量。

图17表明，9号断面以上边坡较陡，m值普遍大于3.5；8号断面至坝前边坡较缓，m值普遍大于10。坝前淤积物较细，且长年不暴露，故边坡较缓。相反，远离坝前的三角洲顶坡上，滩面经常暴露于大气中，边坡较陡。

在以下计算冲刷河槽的库容时，m值的选取为图17中的虚线所示，坝前至8号断面取m=5；9号断面以上取m=3。

（二）冲刷河槽的纵剖面

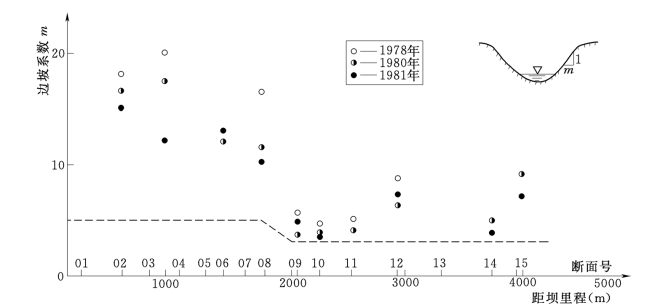
图17　水槽子水库冲刷后主槽边坡系数m

在一定的冲刷流量作用下，水库冲刷河槽纵剖面形状取决于淤积物的抗冲性。当水库淤积物抗冲性到处相同时，在固定流量作用下，最终将得到单一坡度河槽。当各部分淤积物抗冲性不相同时，冲刷的最终剖面将不是一条直线，而是一条反映不同地段淤积物抗冲能力的曲线。实际水库的冲刷纵剖面显然应属于这种情形。水槽子水库库尾为推移质卵石淤积物，中部为粉质土，坝前为黏土，且表层与底部的抗冲性相差悬殊，冲刷纵剖面将是复杂的。另外，纵剖面还随冲刷时间而变化。在冲刷后期冲刷效率较低，对于水量宝贵的水库，还有一个经济比较的问题。

1.不同库段的冲刷纵剖面变化

首先观察近期空库冲刷的结果。近期举行的冲刷流量约50m3/s，冲刷持续时间为2d。水库纵剖面的变化在三个不同的库段各不相同。坝前约1.5km长的库段，冲刷纵比降约为4‰；在中段（距坝1.5～4km）冲刷比降约为1.5‰；上段（4km以上）历次冲刷河槽都变化很小（图6）。各库段纵剖面变化各异的原因显然与相应的淤积物有关。上段库底受披戛河入库的沙卵石推移质的影响，抗冲性强，在坝前水位下降值不大的情况下，溯源冲刷发展至此，河道沿程的冲深已很微弱，在此河段未能造成足够大的比降和流速使之发生冲刷。中段淤积物属于容易冲动的粉土（图8），故冲刷后的比降也较缓。坝前河段淤积物黏性强，冲刷比降也远较中段大。

增设排沙底洞后的空库冲刷，坝前水位下降量将增加十多米。在坝前段，由于底部淤积物抗冲性较上部为大，故冲刷比降下大上小，纵剖面呈一上凸曲线。未来的溯源冲刷发展到中段的下游时，槽底的下切深度也较近期冲刷的下切量大数米，故中段有发生某种平行下切的可能，上段也相应会发生一定的冲深。如果发生这种情况，水库可获得较大的库容恢复量。但在这次计算冲刷量时，为留有余地，暂不考虑中、上段的这种变化可能，仍假定15号断面以上的河槽不冲刷，中段库底的纵剖面近似由坝前段上游端（9号断面附近）的河底与15号断面的固定河底之间的连线决定。

2.不同冲刷历时的纵剖面变化

众所周知，静止状态的泥沙，必须受到某一限度以上的作用力，才能被水流起动，式（2）或图10中的τ0就是水槽子水库黏性淤积物起冲剪切力的试验结果。

（1）起冲比降。文献［10］的试验结果（图18）也说明，当床面剪切力大于某一数值以后，冲刷率E（单位时间单位面积上的冲刷量）才能明显增长。从工程的观点，图18上E值开始明显增长处的剪力，也不妨看作实际的起冲剪力τ0。

图18　试验结果

从图18还可看到，冲刷率大体同水流剪力与起冲剪力τ0之差成正比，即

式（9）中的τ为水流的剪力

式中：γw为水容重；H为水深；i为水面比降。

若利用曼宁公式表示H，则式（10）可改写为

式（11）表明，如果糙率n不变，则τ∝i0.7，但黏性淤积物发生冲刷时，泥沙不是单颗粒起动状态，而是大块的结构性破坏。坡度越大、冲刷越强烈，这种现象越明显，冲刷面越不平整。因此，式（11）中的n值要随i的增加而增加。假定n与i的关系有以下形式

其中α、β均为常数，则式（11）可写成

令K2=γw（αq）3/5，K3=（6β+7）/10，则

目前尚无K3的系统资料，作为近似值，取K3=1，式（9）可写成

式中：i0为某级流量下的起冲比降。

冲刷开始时，坝前侵蚀基面迅速下降，比降i≫i0，发生强烈冲刷，随着冲刷时间的延续，i逐渐接近i0，即（i-i0）趋向于0，冲刷便变弱，乃至停止。

冲刷输沙率qS为

式中：W为冲刷面积。

（2）均匀淤积物的溯源冲刷。文献［11］研究了淤积物抗冲性各处相同，冲刷时输沙率具有式（14）形式的溯源冲刷

式中：qS为单宽输沙率；q为单宽流量；A，m为常数。

在联解河床变形与冲刷输沙率公式的基础上给出了溯源冲刷过程的数理分析计算公式。其中河床比降的变化为

式中：x为距坝里程；l为水库可冲段的长度；Z0为侵蚀基面的下降高度；a2=Aqm/γ，与冲刷流量，淤积物抗冲性有关；，n为自然数；t为冲刷时间。

式（15）中当x=0，即在坝前断面，河床比降向i0接近得最慢，即

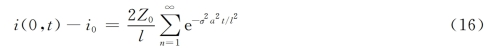
或

(www.xing528.com)

式中：T为无尺度冲刷时间，取决于冲刷时间；QS（T）为无尺度输沙率过程，实质上也是坝前河床比降的调整过程，为冲刷时间的函数。

式（19）说明冲刷过程中河床比降不断变缓，在冲刷时间无限长以后i（0，t）=i0。

式（18）经数值计算，结果如图19。

（3）坝前黏性淤积物起冲比降。前面提到，水槽子水库坝前黏性淤积物抗冲性沿深度而增强。在未来的纵剖面上，不同的深度上有不同的起冲比降i0。

根据图10和图16的结果，按式（10）将抗冲剪力转化为起冲比降，即

其中H的值，取流量为50m3/s，在底宽为10m，边坡1∶5的梯形断面内的临界水深。求得H=0.9m。各层次起冲比降计算结果如表5。

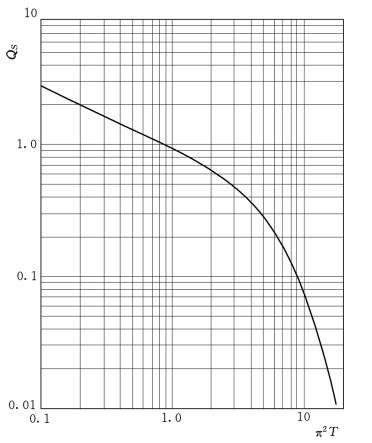
图19　计算结果

表5　坝前淤积物起冲比降

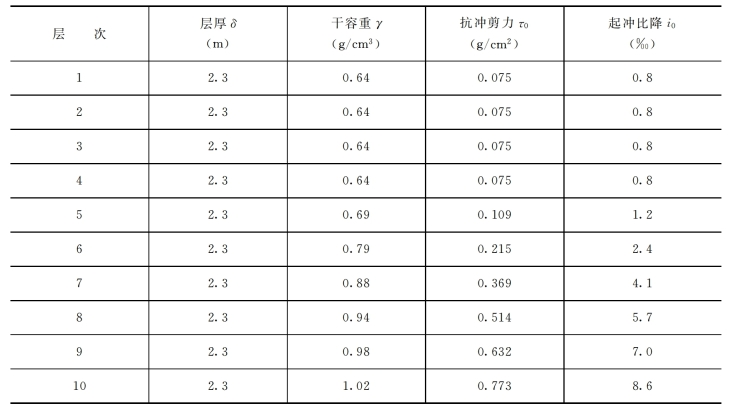
（4）不同冲刷历时的纵剖面。利用式（18），如通过试验得知i（0，t）-i0的数值，也可推求无尺度时间T。式（19）说明，T是冲刷时间、流量、淤积物抗冲性、水库几何特征的综合反映。对同一个水库，除时间以外的诸因素可以认为是固定的，T则正比于冲刷时间t。

近几年来水槽子水库进行的空库降低水位冲刷，流量约为50m3/s，冲刷历时约为48h，冲刷长度l约4000m，坝前侵蚀基面下降量Z0=6m。冲刷后，坝前比降约为4‰，若按表5，i0=0.8‰，则按式（17）有

查图19得π2 T=0.71。

将上述冲刷流量与时间的组合即π2 T=0.7作为一个单位，改变冲刷流量或时间显然都可使T值相应改变，从而获得不同的冲刷效果。以改变冲刷时间为例，当延长冲刷时间N倍时，可按π2T=0.7N来估计冲刷效果。

假定在未来的冲刷中，l值不变（仍认为4000m以上的库区河床不可冲刷）；Z0值按底孔所在高程而相应加大。当底孔为2073m时，Z0值将由原来的6m变为23m。这样，坝前比降的变化按式（17）为

式中：N为时间倍数；T1=0.71/π2，即N=1时的无尺度时间。

表6是排沙洞高程为2073m时，坝前冲刷槽底部（处在最底层淤积物上，按表5，i0=8.6‰）比降随冲刷时间而变化的计算结果。

表6　坝前河床比降i变化计算结果

设坝前各高程上的淤积物冲刷时，i—io均按表6上所列数值而变化，并按第一节关于水库中段纵剖面变化之规定，即可绘制出排沙洞设置在不同高程，冲刷历时不同的水库深槽纵剖面如图20（a）～（c）。实际水库溯源冲刷的纵剖面变化与图20是相似的。与水槽子水库情况接近之东峡水库，在水库形成锥体淤积之后，利用低底孔降低水位十余米空库冲刷［14］，冲刷河槽纵剖面的变化（图21）与图20就十分相似。

图20（一）　冲刷纵剖面变化图

（a）A方案

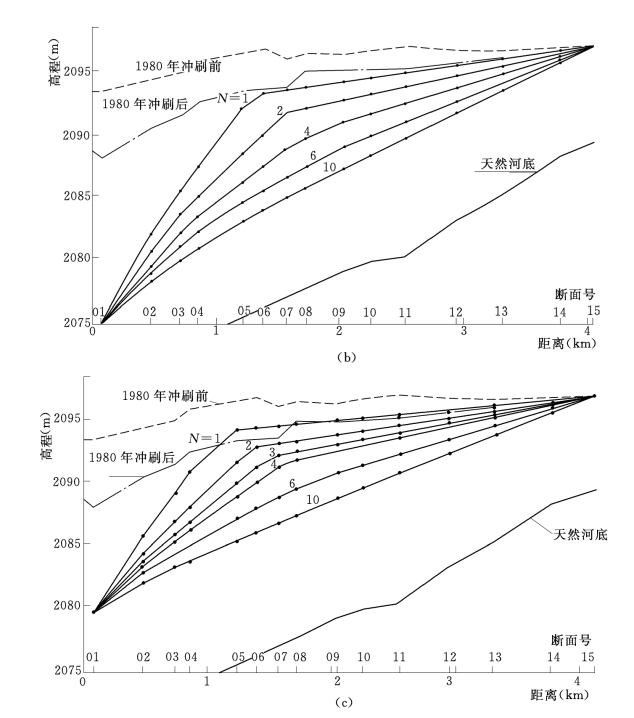
图20（二）　冲刷纵剖面变化图

（b）B方案；（c）C方案

（三）库容恢复数量

按照上述水库冲刷河槽纵横剖面的估算结果，即可求得水库库容的恢复过程如图22（a）～（c）。图22（a）、（b）、（c）分别假定排沙洞在高程2073m，2075m及2080m，以下简称A、B、C（方案）冲刷时间倍数N从1～10，即相当以50m3/s流量冲刷2～20d所获得的库容。

图22说明排沙洞的高程越低，库容恢复的数量就越大，例如A方案（排沙洞高程2073m）较C方案（2080m）可多恢复90万m3的库容。随着冲刷时间的延续，库容恢复的数量逐渐增加，刚开始冲刷时，冲刷量增加较快，到后来冲刷量增速就较慢。以B方案为例，头两天的冲刷可使总库容恢复到160万m3。假定冲刷前原有库容40万m3，则头两天冲刷120万m3淤积物，平均每天60万m3；而冲刷到第9至第12天的4d内（4≤N≤6）冲刷量为34万m3，平均每天8.5万m3，约为头两天冲刷效率的1/7。

图21　4号泄空冲刷强度过程和东峡水库纵剖面

（a）4号泄空冲刷强度过程；（b）东峡水库纵剖面

假定冲刷12d（N=6）经济可取，各方案所能恢复的库容如表7中N=6一栏所列。而冲刷时间为2d，4d，8d的结果分别在N=1、2、4各栏列出。

将表7的结果绘于图23（a）～（d），可在该图查得排沙洞为任意高程的冲刷效果。

（四）排沙洞高程与泄流规模的选择

1.洞口高程与平面位置

图23或表7说明，洞口高程越低，恢复库容的数量越多，而冲沙耗水率也低。

从地形条件出发，A方案（2073m）也许是有可能实现的最低之洞口高程。从表7可知C方案较A高7m，获得的总库容比前者少90万m3，而冲刷单位淤积物的耗水量却多60%左右。

为使排沙洞效率不至于太低，应在其他条件许可时尽量放低洞口高程。洞口不高于2075m时，效率下降就较少。

在蓄水发电的过程中，坝前深槽逐渐被回淤之后，排沙洞前可能保持一个漏斗，顺水流方向边坡约1∶6，侧向边坡1∶4，故排沙洞口的位置最好与电站进水口处于同一断面，必须错开时，以不超过50m为宜。

2.泄流规模

前面所有计算都假定冲刷流量为50m3/s而得。原因是毛家村下泄该流量比较现实。更大的流量要通过区间河道还有其他问题。此外，在该流量之下，有几次空库冲刷的实测资料，用这些资料推断未来相同流量的结果可靠性要高一些。

图22　水库库容的恢复过程

（a）A方案；（b）B方案；（c）C方案

从表7结果看来，用50m3/s来冲刷，效果也还是可以的。但是，这一流量未必就是最优的冲刷流量。悬移质淤积物的冲刷，冲刷输沙率与流量的关系不完全是线性的，即式（14）中的m值，约在1与2之间，文献［13］得到m=2。这意味着，以相同的水量来冲刷，流量大的效率也高。东峡水库冲刷资料表明，大流量冲刷效率较小流量高数倍［12］。故水槽子水库今后很值得争取实现去用较大的流量冲刷。从式（19）也可看到，增大流量可以与延长冲刷时间等效，故排沙洞泄流能力大些，可给管理运用带来更大的灵活性。以礼河是个极好的坝址，应当为电站群今后的百年大计留下更多的余地。譬如，让二级水库能利用区间洪水来冲沙，今天虽然还办不到，将来还是一个可能实现的措施。

据粗略估算，明流泄流量分别为50m3/s、100m3/s、150m3/s与200m3/s时，相应的洞子断面（方形）约为3.9m×3.9m、5.1m×5.1m、6.0m×6.0m以及6.7m×6.7m。

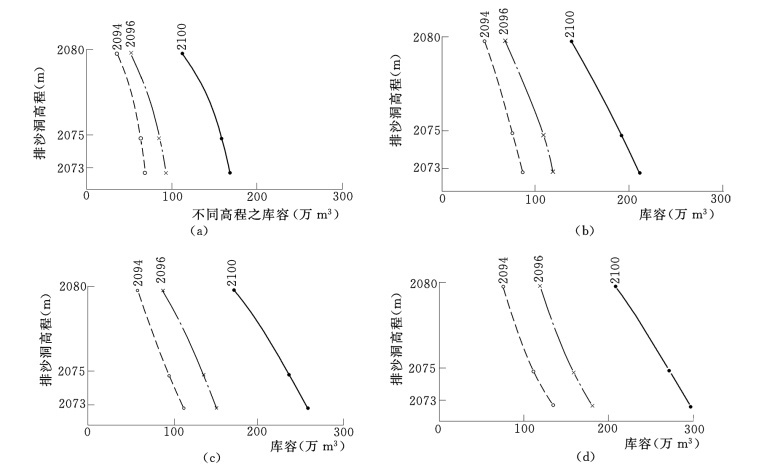
图23　不同排沙洞高程的库容恢复量

（a）冲刷时间N=1；（b）冲刷时间N=2；（c）冲刷时间N=4；（d）冲刷时间N=6

表7　各方案冲刷效果比较

*冲刷流量为50m3/s的冲刷天数。
**淤积物平均干容量按1000kg/m3计。

综上所述，建议考虑以明流状态通过100m3/s或更大的流量作为排沙洞应具有的泄流能力。