FEC数据分配优化探讨

如何设计合适的算法求解形如式（4.8）的优化问题，文献[5]进行了一些分析和讨论，比较了一些寻优算法，如爬山算法、粒子群算法等的优劣，分析了算法复杂度与解的精度之间的关系。这些算法虽然可以逼近最优解，但得到的解为局部最优的概率也较大。此外，这些算法复杂度较高，如直接用于SVC传输系统中易导致较大的时延，降低视频传输的实时性。而文献[7]直接采用遗传算法对SVC中各层分配FEC数据的问题进行了优化，指出遗传算法在解决这类问题时具有解的精确度高、易于实现等优势。事实上，遗传算法虽然具有鲁棒性强、适应性广的优点，但也在寻优过程中存在收敛速度慢及过于偏好某些适应度大的个体，易导致“早熟”的问题。针对遗传算法的这些不足，考虑到自适应遗传算法（Adaptive Genetic Algorithm，AGA）在寻优速度及求解精度方面的优点，本书采用AGA求解式（4.8）的优化问题。最后得到FEC数据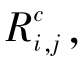 i=1，2，…，M，j=1，2，…，N，提高了SVC传输的抗码性能。具体算法在以下几节进行了分析和描述。

4.3.2.1 自适应遗传算法

本质上，遗传算法是一种基于生物进化机制的自适应概率优化技术。它以达尔文的生物进化论和孟德尔的遗传变异理论为基础，通过对生物遗传过程中的自然选择、交叉及变异过程的模拟，经过多次迭代使个体得到优化，最后逼近最优解。遗传算法可表示为以下形式[8]：

其中，C为个体的编码方法，E为适应度函数，P0 为初始种群，φ为选择算子，Γ为交叉算子，ψ为变异算子。

适应度函数E是遗传算法中非常关键的一个部分，好的适应度函数能够指导将非最优的个体进化到最优个体，并可解决一些遗传算法中常见的问题，比如过早收敛、过慢结束等问题。在对染色体适应度值进行评估的基础上，选择算子φ用来确定按何种方式从父代染色体中选择合适的染色体作为子代的遗传算子。目的是在进化过程中消除优良基因的损失，提高全局收敛能力。交叉算子Γ通过模拟自然界有性繁殖的基因重组原理，在算法执行过程中尽量保留原始特征。变异算子ψ是在模拟生物进化过程中，染色体上某位基因发生的突变现象，其作用在于将优良基因遗传给下一代个体，并生成具有新结构的个体，进而改变染色体的结构，达到变异的目的。

可以看出，由于能够对多个解进行评估，遗传算法有较强的解决复杂问题的能力，同时也具备计算精度高、不需要目标函数可导的特点。但由于执行过程中的收敛现象，可能使整个种群染色体上的某位或者几位都过早收敛到一个固定的值，导致未成熟收敛，降低全局搜索能力[9]。此外，遗传算法在处理具有较复杂的约束条件的优化问题时效率较低，采用何种约束条件处理方法对提高遗传算法的优化能力具有重要意义。

因此，针对经典的遗传算法中参数固定的不足，自适应遗传算法在寻优过程中根据进化代数及相应的适应度自适应地调整交叉算子及变异算子，使算法的全局寻优能力与局部寻优能力随着进化的代数而动态调整，加快了进化的速度，达到了保护优良个体，防止早熟现象的目的。在以下两小节中，对自适应遗传算法中的参数进行了分析，并提供了完整的求解步骤。

4.3.2.2 适应度函数与编码方法

首先，为便于采用自适应遗传算法进行求解，将带多约束条件的式（4.8）转换为无约束优化问题。将约束条件式（4.9）、（4.10）及式（4.11）分别改写为

然后，引入如下形式的惩罚函数：

式中，k与mi（i=1，2）为惩罚因子。从而将形如式（4.7）的优化问题转化为如下形式的无约束优化问题：(www.xing528.com)

其中，Qmax为无NALU丢失时该GOP的PSNR。惩罚因子的取值可以随着进化过程的进行而自适应地进行调整，也可以设定为常数。考虑到提高算法的实时性，本书对m1 与m2 取经验值[10]，分别取3.5，4。

自适应遗传算法在执行过程中，由适应度函数来指导搜索方向。因此，在上述分析的基础上，选择如下函数作为自适应遗传算法的适应度函数：

此外，为便于在进化过程中实现交叉、变异等操作，采用二进制编码算法。考虑到SVC中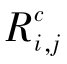的取值为范围为[0，n]，故用len =「log2n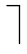位二进制数来表示其大小，其精度为n/（2len-1），个体的编码长度可表示为M·N·len，初始种群中个体的数量为μ。

4.3.2.3 自适应遗传算法的参数选取

为避免标准遗传算法容易造成求解过程的早熟与局部收敛现象，自适应遗传算法在进化过程中，根据种群中个体适应度的值自适地改变交叉算子和变异算子。当个体的适应度高于平均适应度时，该个体的交叉与变异算子的值较小。反之，将其取较大的交叉与变异算子[11]。此外，选择算子对遗传算法的收敛速度有着显著的影响，为避免整个群体的适应度值的方差过大或过小，导致进化过程过早收敛或过于抖动。在式（4.19）的基础上，为进一步保留更多的优秀个体，采用下式计算个体适应度：

其中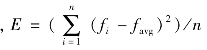表示种群适应度值的方差，fmax与favg为上一代种群的最大适应度与平均适应度。个体复制时，按概率 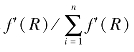进行选择操作。显然，引入E会增加算法的计算时间，但在较大程度上可避免超级个体以较高的概率出现而导致过早收敛。

另外，自适应遗传算法在进化过程中应保持种群的多样性以防止出现早熟现象，同时降低较优的个体处于停止不变状态的概率。按式（4.21）与式（4.22）自适应地选择交叉算子Pc和变异算子Pm：

其中，f′表示参与交叉的两个个体中具有较大适应度值的个体，f表示待变异个体适应度的值。Pc1，Pc2和Pm1，Pm2为常量，分别表示自适应遗传算法运行过程中交叉和变异的速率。

此外，本章采用实验的方法取得上述常量的值。从初值为0 开始，使Pc1，Pc2以0.1 为步长； Pm1，Pm2 以0.001 为步长。在区间[0，1]中按式（4.21）和式（4.22）计算交叉和变异算子，以E≤10-3为终止条件，最后求得上述常量的值为Pc1 =0.7，Pc2 =0.9，Pm1 =0.13，Pm2 =0.002。

事实上，针对上述常量的取值，文献[12]也进行了分析和实验，并提供了参考值。该文献指出，其值越大，算法的收敛速度也越快，但走向局部最优的概率会增大； 反之，值越小，算法收敛速度也越慢。总的来看，其取值与算法的具体应用环境有一定关系。考虑到SVC的特点，本书在SVC传输的实验环境下对上述常量的值进行计算，能更好地适应具体的面向SVC的视频传输系统。