SVC平均失真计算方法优化

由于SVC的时间可伸缩编码目前广泛采用的是层级B帧编码技术，时间分层中的低层对高层的正确解码起着关键作用。如低层数据丢失，即使解码器采用了错误隐藏技术，也会将错误扩散至高层。同时，MGS 为解决编码过程中的漂移问题，引入了关键帧[5]。采用关键帧作为同步的参考点，使漂移的扩散范围仅局限于同一GOP中，避免了误差的累积和扩散。此外，SVC选择质量最高的帧作为关键帧的参考帧，同时也作为非关键帧的基本层和增强层的参考帧。与此类似，低层的数据在部分丢失后，其错误也会扩散至高层。因此，在会发生数据包丢失事件的网络传输环境下，计算SVC在传输过程中由于丢包而造成的失真是设计高效的纠错方法的前提。显然，SVC由于丢包而造成的失真可表示为

其中，di，j表示时间层和质量层分别为i、j的NALU丢失后造成的失真，其丢失的概率为p。p的大小可由Gilbert模型计算而得[6]。M，N分别为时间层与质量层的数量。为求得di，j的值，考虑时间层数据丢失后的错误扩散区域，采用下式计算时间层中各层数据丢失后的失真扩散程度：

其中，c为常数。

然后，将质量层中各层数据丢失后的失真扩散程度表示为

从上述两式可看出，失真扩散程度的大小与丢失数据所在的层有关，这也与SVC的编码原理相一致。但对于参数c的取值，一般是根据SVC测试序列的传输实验得到其经验值。但这忽略了各层数据之间的关系，带有极大的随意性。本质上，正如图4-2 所显示的，不同层的数据所属特征在SVC的扩展数据头中得到充分的体现。因此，在分析SVC中扩展数据头结构的基础上，采用下式计算c的值：

可以看出，为计算c的值，必须对SVC中NALU的扩展数据头进行解析。事实上，对该数据头的解析可在网络应用层中实现，且复杂度较低，带来的编码时延也可以忽略。根据式（4.5），可将式（4.2）中的di，j表示为(www.xing528.com)

其中，参数ν1 的取值与时间及质量层的数量有关，具体取值在实验过程中根据编码器JSVM的编码参数确定，在分析SVC传输失真时提供的方法中，将ν1 取0.45。因此，式（4.2）可改写为

最后，在最小化D的前提下将分配Rci，j的问题转化为如下带多约束条件的优化问题：

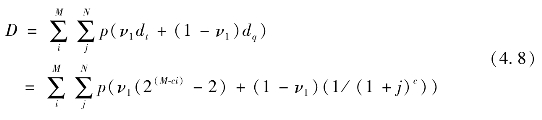
同时有如下约束条件：

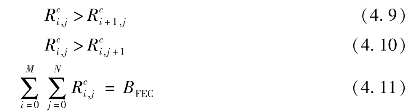
其中，BFEC为校验位的总和，即FEC数据，也称之为冗余数据。BFEC的取值与两个因素有关，一是采用了纠错操作的视频数据包的个数，二是采用何种编码方案的FEC码。此外，采用了差错保护的视频数据包的数量Br与网络丢包率p紧密相关，在某个固定的时间段t内，二者呈线性关系，可表示为

其中，参数ν2 和ν3 分别取6.93t和104.7t。一般来讲，当网络丢包率p大于15%时，在时间段t内，Br与全部视频数据的比值趋近于95%。此外，考虑到许多视频接收设备处于突发错误较多的无线网络传输环境中，因此本章方法中采用的是RS（204，188）码，相应的冗余数据比例可以认为是16/204。故最终BFEC的值可以表示为Br（16/204）。