如何选取蠕变模型的参数？

蠕变模型参数通常来源于试验或者实测资料。如何根据试验曲线确定这些参数是一个比较重要的技术问题：如果参数取值合理，则解答准确的可能性就高；如果模型参数质量差，则结果的准确性就一定差。

图6-4是一个盐岩圆柱试件蠕变试验结果曲线，图中标出了试验的侧压力、温度、加载应力变化幅度等各种条件。横轴是时间，纵轴是蠕变应变。

由于要分析的问题是溶解开采引起的岩石变形，分析过程中开采引起的应力变化很大，因此计算时选用了幂形式的应变硬化蠕变模型。

接下来要在试验曲线上选取原点以外的3个点，3个点处的斜率可以

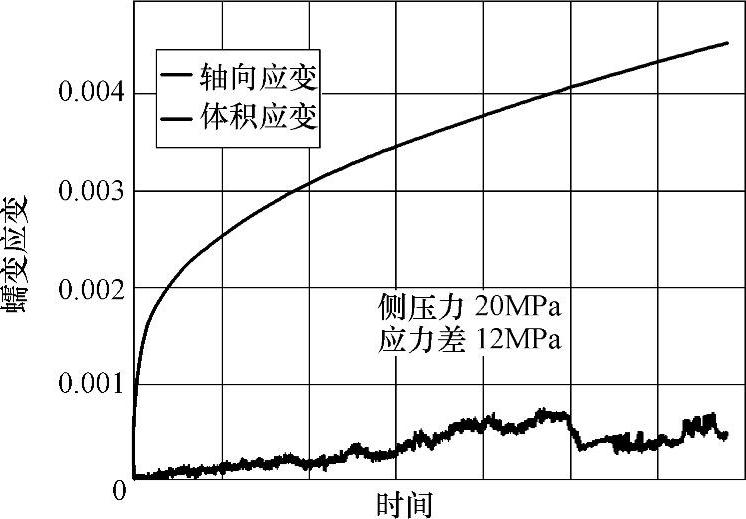
图6-4 蠕变的试验曲线

近似作为该点的蠕变应变率，从而参考式（6-4）可以建立3个方程，求得3个待定系数A、n和m。

根据图6-4求得的上述蠕变模型参数为

A=10^-21.8，n=2.667，m=-0.2 （6-6）

从而可以确定相应的蠕变模型为(www.xing528.com)

式中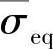，是Mises等效应力。为了避免A的取值过小引起数值计算误差，这里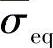的单位取MPa，时间单位取年。

为了初步检验模型的正确性，有必要对上式进行积分，然后作出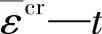全量形式的曲线，再与试验曲线进行比较。这里首先需要确定Mises等效应力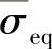的值。由图中标注可知，侧压力为20MPa、压力差为12MPa，此时Mises等效应力的值约为7MPa。将代入上式，对时间积分可得

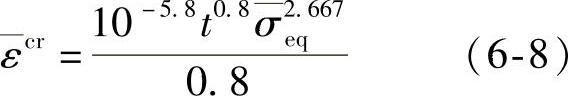
相应的图形如图6-5所示。

图6-5 由式（6-8）求得的蠕变曲线

对比图6-4与图6-5，发现图6-4试验曲线在前5天以内变形初期的蠕变应变率很高；在5天以后的加载后期则趋于平稳。图6-5的近似简化模型曲线与试验曲线相比，在初期差别较明显；在变形后期则很接近。由于本章算例涉及的时间跨度为3.5年，远远大于5天的初期阶段，因此简化模型在大部分时间段上满足要求，可以说是一个合理的模型。