力学模型研究：基于对称性的井孔失真分析

为了能够较详细地模拟围绕射孔周边的岩石的力学行为，考虑到射孔尺寸很小，仅有0.5in，故取厚度为0.1524m（0.5ft）、半径为3m的一片岩石进行三维有限元弹塑性固结分析。考虑到模型的对称性，仅取1/2模型分析，如图5-2所示。

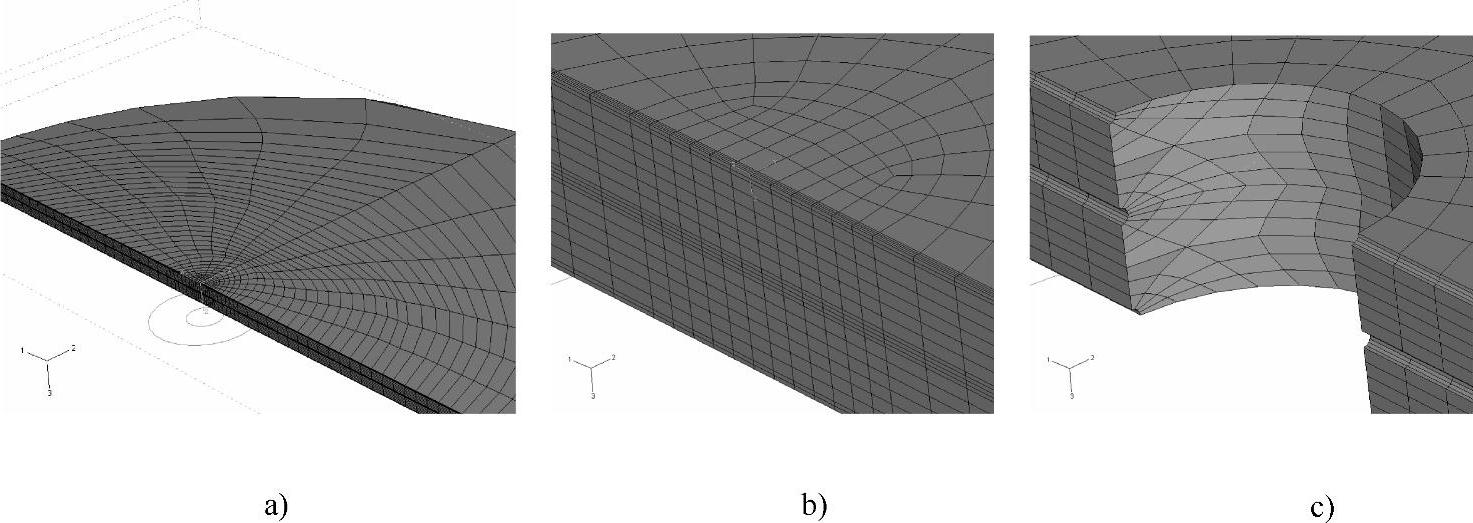
图5-2 模型网格及局部放大图

a）模型初始网格 b）井孔处局部放大图 c）移除井孔及射孔单元

边界条件如图5-3、图5-4所示。在中间对称面上，y方向的位移为零；在外缘边界上，水平位移为零；在底面上，z方向的位移为零；在上表面上作用有均布压力。初始条件为：初始孔隙比为0.351，初始孔隙压力p=3.79212×10⁷Pa，初始地应力为σ_x=-48263338Pa，σ_y=-41368575Pa，σ_z=-55158199Pa，切应力分量为零。外缘边界上的孔隙压力为p=3.79212×10⁷Pa，对称面设为不透水边界。流动压力为p_d=3.68×10⁷Pa。在射孔完成之后的固结过程，射孔表面上将作用有其值为流体压差的均布面力。射孔表面的孔隙压力边界的值也等于流体压差。岩石材料的弹性模量和泊松比分别为E=9.37×10⁹Pa，μ=0.22。

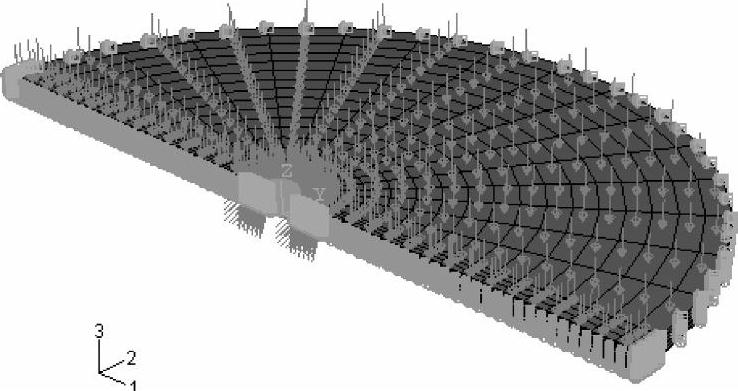
图5-3 模型的几何形状及约束示意图

(www.xing528.com)

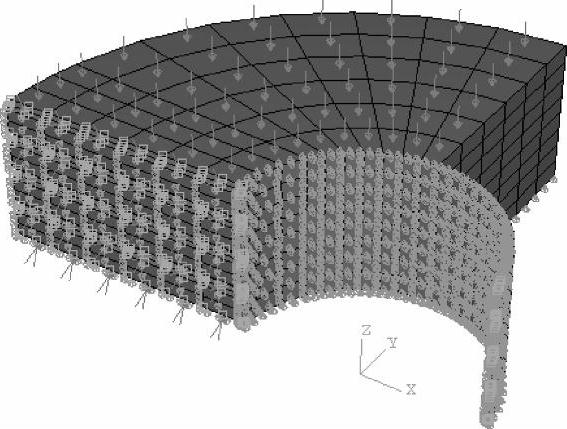
图5-4 模型中采用了一层弹性膜 单元模拟套管的不透水特性

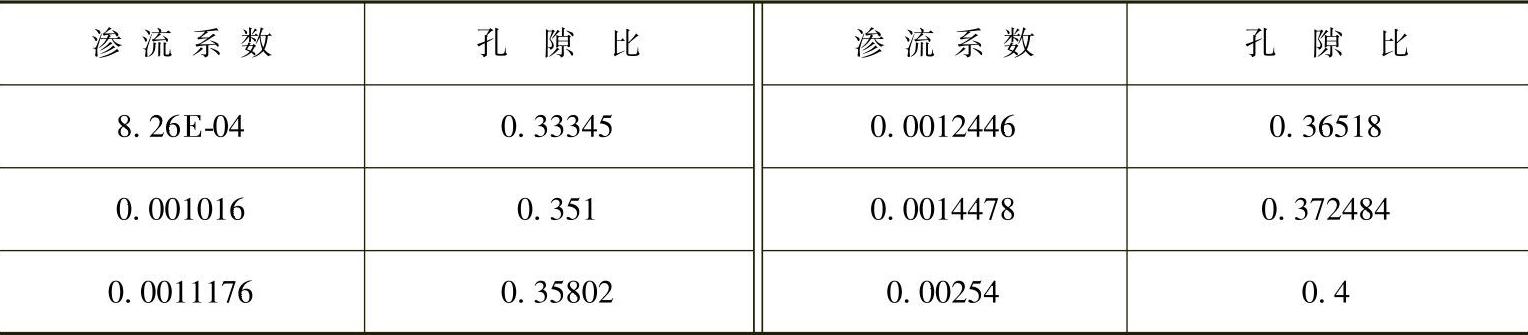
渗流系数k随孔隙比的变化规律见表5-1。

表5-1 渗流系数k随孔隙比的变化规律

岩石的强度参数分别为：内摩擦角φ=25°，扩容角θ=10°，粘结强度c=5×10⁵Pa。

为了模拟套管的作用（即刚度较大、不透水），在模型中采用了一层弹性膜单元附加在井孔岩石边界外侧。当井孔和射孔完成后且固结过程开始时，膜单元在水平面内被赋予位移约束。图5-4所示为每英尺8个射孔的几何模型。