结构有限元分析：钢球卡入衬板缝隙问题优化

如上文所述，由于衬板的初始缝隙较大，钢球在位于筒内底部时由于缝隙张开的作用进入缝隙。之后，由于钢球在缝隙中能形成摩擦自锁力学关系，从而致使钢球在随筒体转动到顶部时，缝隙有闭合趋势时产生支撑膨胀。由于缝隙的尺寸不断变大，因此可以判断：钢球和缝隙之间在顶部位置时存在类似过盈配合的关系，钢球对缝隙两侧衬板有挤压外撑作用。这一外撑作用使得初始就比较大的缝隙逐渐变得更大，同时加剧了衬板所在部位的筒体的变形。

根据上述分析，本次计算采用在缝隙处加入矩形截面钢条的方法模拟钢球嵌入缝隙的现象。用矩形截面钢条代替成排的圆形钢球能够在保证整体力学效果的合理准确度的前提下，明显降低有限元的接触模拟的计算工作量。

图4-16为卡入缝隙的钢条的示意图。可以看出，卡入缝隙的钢条与衬板形成过盈配合，过盈量随着筒体转动、缝隙张开闭合循环、小钢球卡入的深度增加而逐渐增加。根据破坏时的图片显示，小钢球可以卡入到缝隙的底部，因此，相对与初始缝隙宽度的过盈量是相当大的。这里取过盈量为2mm（即钢条宽度为22mm，缝隙宽度为20mm，钢条的宽度大于缝隙的宽度2mm），进行工作载荷下的三维ABAQUS有限元变形和应力分析。模型网格、载荷、边界条件都不变，只是在顶部的缝隙处加了一个轴线弧长为185mm的弧形钢条，模拟卡入的小球的作用。

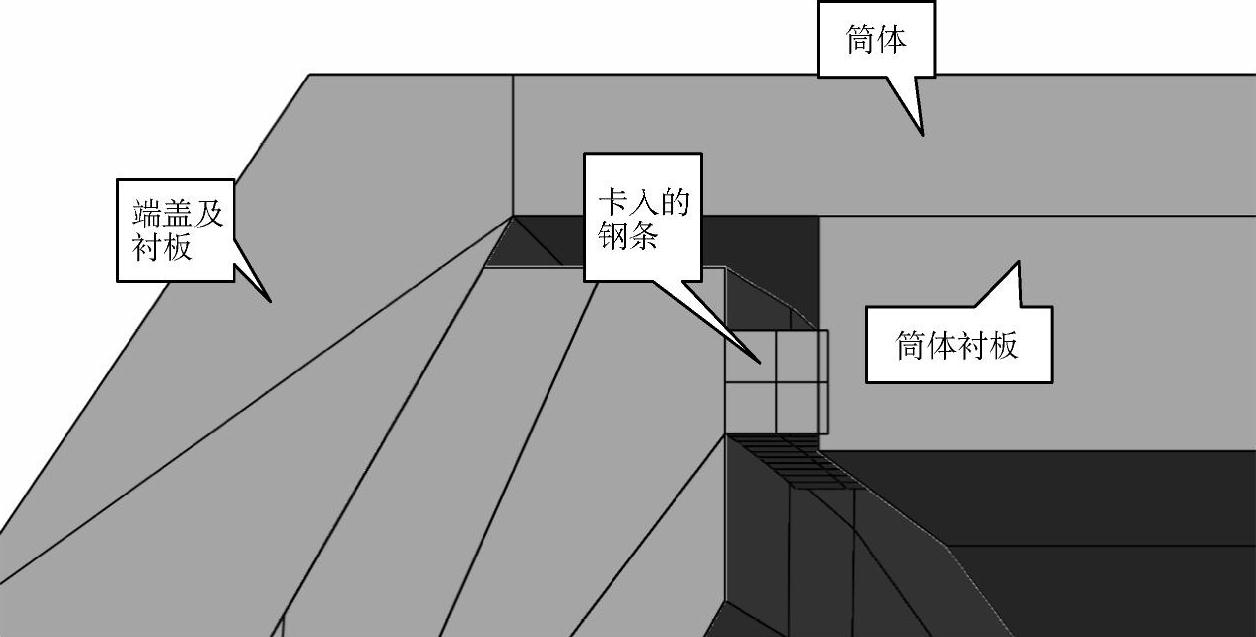
图4-16 卡入缝隙的钢条示意图

计算结果如图4-17～图4-22所示。由图4-17可知，小钢条及周围衬板及筒体的轴向应力S11幅值明显大于周围一定距离之外的材料点的应力幅值，出现了强烈的应力集中。

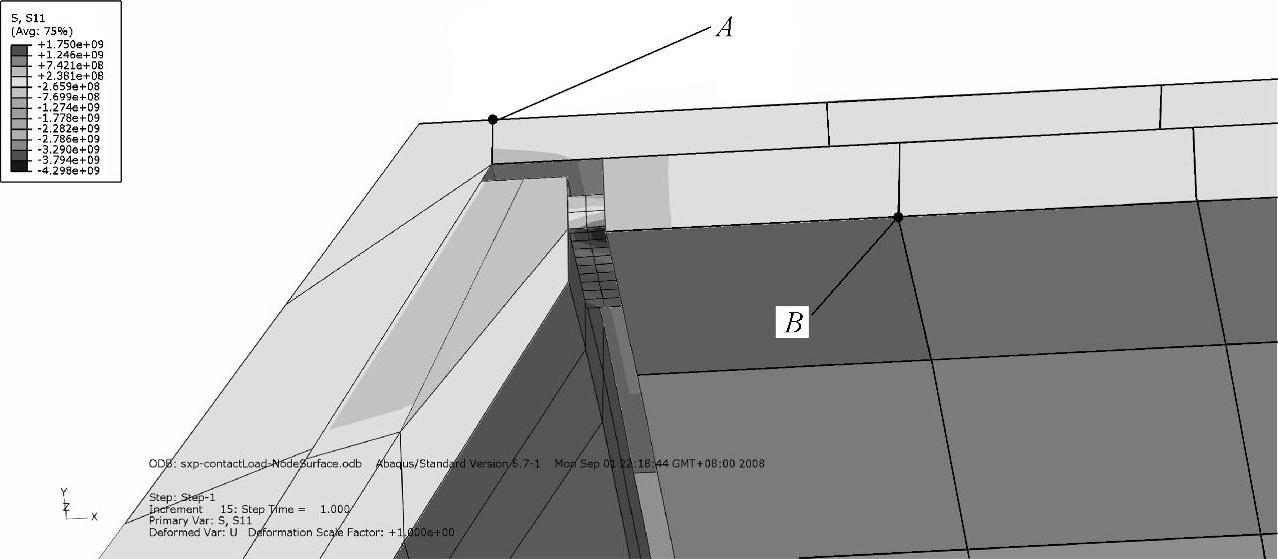
图4-17 小钢条、周围衬板及筒体的应力分量S11分布结果（三维，局部放大）

分别在图4-17的A点和B点作环向路径（周长），以小钢条的中心（即筒体横截面的顶点）为原点，作出的轴向应力分量环向分布图。图4-18是以A点为原点作出的筒体外表面上的S11分量的环向分布图。图4-19是以B点为原点作出的筒体衬板上的S11分量的环向分布图。

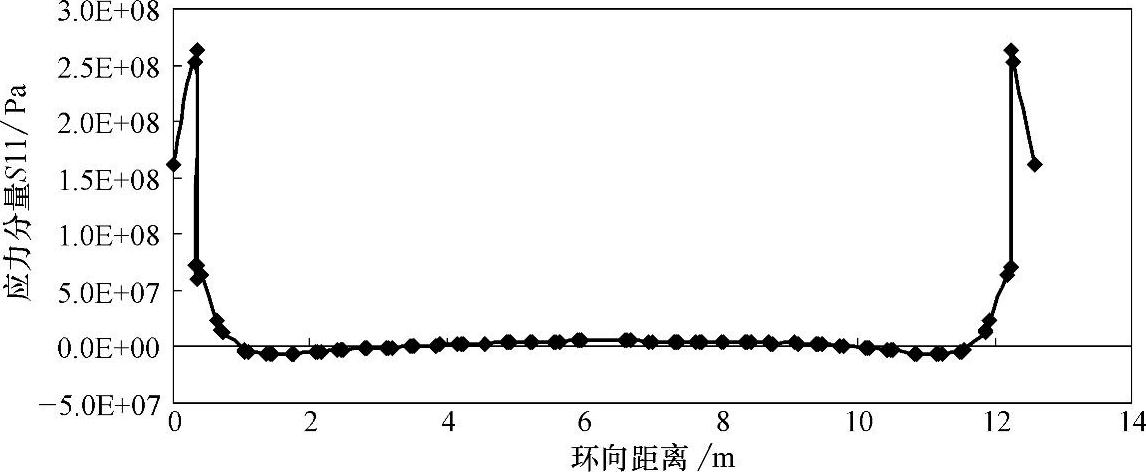
图4-18 沿筒体外表面的轴向应力分量S11分布

由图4-18可见，筒体上各点仅在钢条卡入的区域附近，有超过50MPa的较大应力分布，且最大值达到264MPa。在钢条所影响的局部（2m左右的周长）之外，其他区域上筒体上沿过A点的圆周路径上各点的应力都在10MPa以下。在筒体轴线中心截面处的顶部顶点和底部顶点的应力S11的值仍然分别是19MPa和-25.6MPa。

由图4-19可见，在衬板上各点，仅在钢条卡入的区域附近约2m的周长范围内，有超过50MPa的较大应力分布，且最大值压应力最大达到164MPa。在钢条所影响的局部（2m左右的周长）之外，其他区域上的应力S11都在10MPa以下。

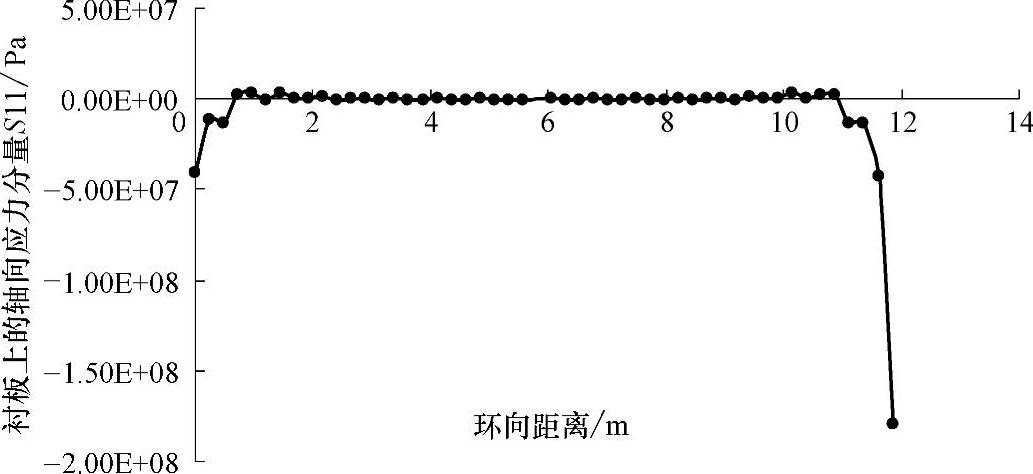
图4-19 沿筒衬板外表面的轴向应力分量S11分布

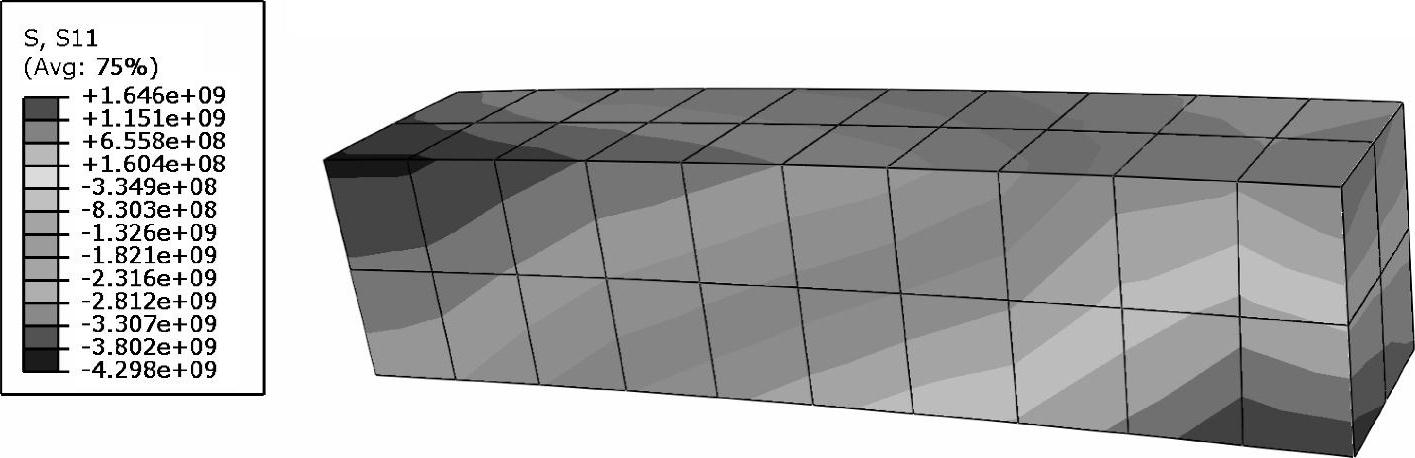
钢条上的应力和应变分布如图4-20～图4-22所示。从图4-20看出，钢条的轴向应力分量超过1000MPa，而图4-21中的应变分量达到0.009208，接近1%。

(www.xing528.com)

图4-20 钢条内应力分量S11的分布图

图4-21 钢条内应力分量LE11的分布图

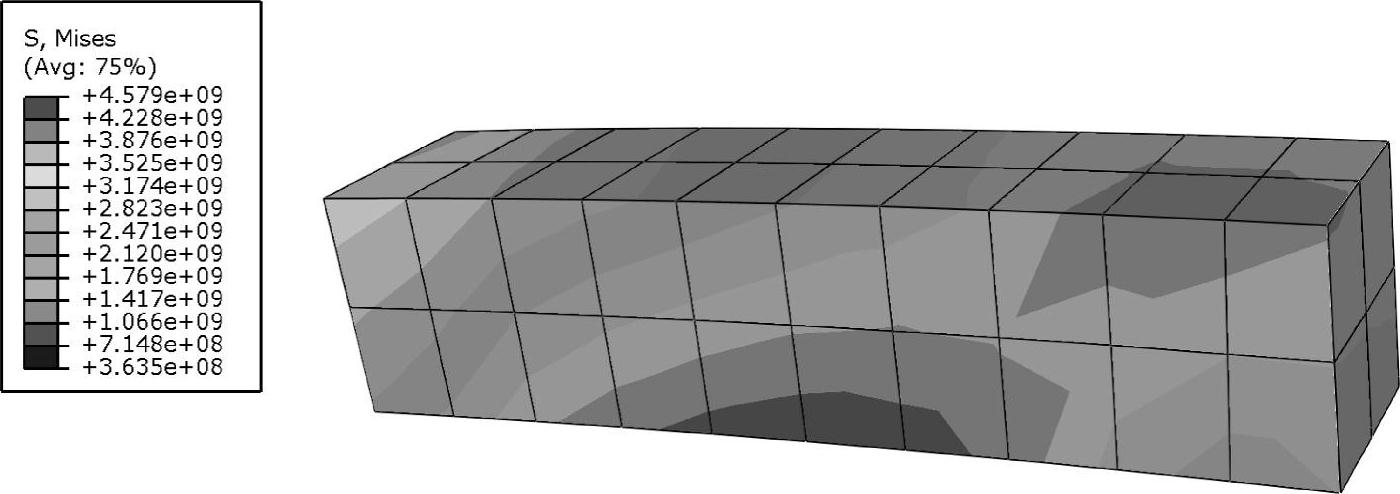
图4-22 钢条内Mises等效应力的分布图

由图4-22可见，在钢条内，作为塑性变形判断准则的Mises等效应力的值超过1000MPa，远远大于锰钢的初始塑性屈服强度，表明钢条内部将产生塑性变形。这与实际情况是相符的：从破坏了的筒体实体现场可看到，钢球在缝隙内被挤扁，即发生了塑性变形。

从上述应力分析中可看出，最大应力为沿轴向的拉应力S11，对于拉应力引起的疲劳破坏，在正常工作情况下，最大满载达到50%容积装载量时，最大拉应力为19MPa，最大压应力为25.6MPa，因此磨煤机的疲劳失效属于非对称正应力引起的疲劳循环，且

对于此类非对称应力的疲劳分析，一般应根据实测疲劳曲线确定材料疲劳强度值。考虑到文献的数据，进一步采用保守设计的取法，疲劳强度可取

σ_-1=0.28σ_b （4-11）

式中，σ_b是材料的静强度极限。从文献中得知，对于Q235钢材，其屈服强度最小值为

σ_b=400MPa （4-12）

而

σ_-1=0.28σ_b=0.28×400MPa=112MPa （4-13）

在正常工作情况下，即使是最大满载达到50%容积装载量，最大拉应力也只有19MPa，最大压应力仅为25.6MPa，小于上述许用疲劳应力值112MPa。

在有钢球卡入缝隙的情况下，按照上述三维有限元分析的结果，筒体上的材料点在钢球附近局部区域有最大轴向拉应力分量264MPa，而在压应力区，最大值仍然是-25.6MPa。而264MPa远远大于112MPa的许用应力值。