电压的各影响因素进行分析

单相接地过电压是线路在发生单相接地故障时（故障相两侧断路器还未断开），在健全相上产生的瞬态过电压。虽然发生过程简单，但影响因素较为复杂，接地因素（包括接地电阻和接地点位置）、线路输送功率、线路杆塔的参数、高抗补偿度和两端电源阻抗特性等均可能会对单相接地故障过电压产生影响。其中，接地因素、线路输送功率、线路杆塔参数和高抗补偿度等因素对该过电压的影响较为简单，为基本影响因素；线路两端等效电源的阻抗特性对单相接地故障过电压的影响较大，为重点影响因素。

下面对该过电压的各影响因素进行分析。

6.2.3.1　基本影响因素

1）接地电阻和接地位置影响分析

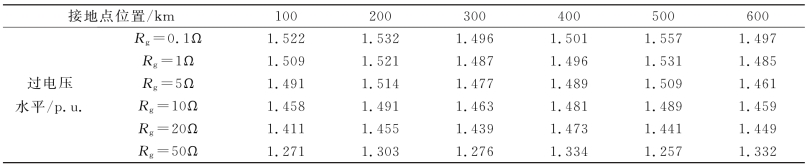
单相接地故障过电压是由接地故障产生的，接地故障因素主要包括接地位置和接地处的电阻值Rg两方面，下面分别就这些因素对过电压的影响程度进行分析。当接地故障因素发生变化时，单相接地故障过电压计算结果如表6-8所示。

表6-8　不同接地因素下的单相接地故障过电压计算结果

结果表明：

（1）接地点相同时，接地处电阻值Rg越小，过电压幅值则越大，这是因为接地电阻越小时，接地暂态过程越激烈，过电压也就越高。

从严考虑，以下研究中接地电阻值采用0.1Ω。

（2）接地电阻相同时，不同接地点下的过电压幅值有差异，这是由于在不同位置出现单相接地时，从接地点向线路看进去的阻抗分布存在差异所引起的。

因此，在研究单相接地故障过电压时，应考虑接地位置的变化对该过电压的影响。

2）输送功率影响分析

在出现接地故障之前，线路可能处于不同输送功率的运行状态，下面分析线路上输送功率是否会对该过电压产生影响，计算时保证不同功率下两端母线电压一致，结果如表6-9所示。

表6-9　不同输送功率下单相接地故障过电压计算结果

由表6-9可知，随着线路输送功率的变化，相同接地点情况下线路上的过电压幅值变化很小。当输送功率从0增加至3000MW时，相同接地点上的过电压幅值前后相差不超过0.02p.u.，可忽略。

鉴于此，以下研究中输送功率均采用0MW的空载状态。

3）线路杆塔参数影响分析

分析不同导线型号以及杆塔参数对单相接地故障过电压的影响程度，计算时保证模型其他条件一致，结果如表6-10和表6-11所示，表中的过电压值均为该条件下整条线路上不同位置发生接地故障时的最大过电压值。

表6-10　不同导线型号下单相接地故障过电压计算结果

表6-11　不同杆塔参数下单相接地故障过电压计算结果

结果表明，随着导线型号的变化，单相接地故障过电压幅值变化很小，最大相差不超过0.006p.u.，可忽略；当杆塔参数明显变化后，过电压幅值改变也较小，最大相差不超过0.04p.u.，对计算结果不会产生实质性的影响。

鉴于此，以下研究中导线型号采用LGJ-500/35，线路杆塔采用特高压常用猫头塔型。

4）高抗补偿影响分析

分析不同高抗补偿度对单相接地过电压的影响程度，计算时保证模型其他条件一致，结果如表6-12所示。

表6-12　不同高抗补偿下单相接地故障过电压计算结果

结果表明，高抗补偿对单相接地过故障过电压有一定的抑制作用，补偿度越高，单相接地故障过电压越低。当补偿度小于30%时，过电压随着补偿度的升高明显降低；当补偿度大于30%时，增加补偿度对过电压的影响就很小了，此时随着补偿度的增加过电压仅略有下降。目前，特高压线路高抗补偿度一般在80%～90%之间，从严考虑，以下研究中线路均采用80%的高抗补偿度。

6.2.3.2　电源阻抗特性分析

1）电源阻抗范围界定

实际上，电源阻抗特性会对单相接地故障过电压产生较大影响，目前在单相接地故障过电压工程计算中通常仅计算最大、最小和正常运行方式等少数典型情况，这是不够全面的。因为他们主要反映的是负荷的变化，但前面的分析表明负荷变化对单相接地故障过电压的影响很小，但电源阻抗特性却会对单相接地故障过电压产生重大影响。因此必须界定特高压交流系统等效电源阻抗的范围，研究它对单相接地故障过电压的影响。

目前，我国特高压交流电网处于建设初期，在两个超高压电网基础上架设特高压线路来进行点对点输电是其主要的模式。因此，本节主要研究该种情况下电源阻抗的等效问题。在图6-5所示模型中，电源阻抗通常包含500kV侧电网电源等效阻抗、变压器自身阻抗以及第三绕组侧的低压容抗等，计算复杂且难以准确界定。本节在综合考虑了超高压电网的等效情况、特高压变压器及其低压侧容抗的分布后，得出等效后的电源阻抗范围，等效方法如图6-9所示。

下面具体分析影响等效后电源阻抗的三个因素的范围[12]。

首先，分析500kV等值电源的X1（正序阻抗）范围。资料表明，500kV系统的短路电流通常都在12.5kA～75kA范围之内，由短路电流计算公式（6-2）可得出等效X1范围约在3.85～23.1Ω之间，本节偏严考虑10%的误差，取X1范围在3.5～25.4Ω之间。

式中：X1为正序电抗；U1为系统线电压，取值500kV；Ik为短路电流。

其次，分析500kV等值电源的X0/X1（零序阻抗/正序阻抗）关系。充分考虑500kV线路和变压器该比值的情况，偏严考虑，将该比值范围定为0.5～3.5[13-14]。(www.xing528.com)

最后，采用我国特高压示范线路的变压器参数，并考虑一台变压器运行或两台变压器并联运行的两种情况，将变压器低压侧容抗范围分别定为：一台变压器，低容1000Mvar～低抗1000Mvar；两台变压器，低容2000Mvar～低抗2000Mvar。

在上述参数范围内，通过仿真得出单相和三相短路电流幅值，然后采用短路电流公式反演计算并适当扩大取整，得出等效后特高压电源的X1在40～180Ω范围内，X0/X1在0.4～1.4范围内，如图6-9所示。

图6-9　1000kV等效电源阻抗计算示意图

由于上述三个参数范围的选择较为宽裕，包含了绝大多数特高压交流系统的电源阻抗情况。因此，可以认为在此基础上得出的特高压等效电源阻抗范围是宽裕的，在此范围内进行过电压极大值的研究，得出的最大过电压幅值也是偏严格的。

2）过电压极大值的电源阻抗确定

针对图6-5所示的模型，在上文得出的电源阻抗范围内，研究电源阻抗对单相接地故障过电压的影响情况，寻找过电压最大时的电源阻抗特性，得到求取单相接地故障过电压最大值的方法。

（1）单相接地故障过电压与电源零正序阻抗比的关系

保持E1端电源阻抗不变，只改变E2端电源的阻抗，计算结果如表6-13所示。计算时在沿线等距设置20个接地点，求取各个接地点故障时的沿线最大过电压值，20个沿线最大过电压值的最大值即为该种电源阻抗情形下的单相接地故障过电压值。

表6-13　E2端电源阻抗发生变化时单相接地故障过电压计算结果

由表6-13可知，电源阻抗的变化对单相接地故障过电压影响较大，其中X0/X1阻抗比越大时，该过电压就越大。同时，进一步计算表明，保持E2端电源阻抗不变时仅改变E1端电源阻抗的情况下也有上述规律。因此，可以认为，当X0/X1阻抗比达到最大值1.4时，单相接地故障过电压达到最大。理由分析如下。

单相接地故障过电压是在线路产生接地故障后，在单相接地工频过电压的基础上产生的，因此，与单相接地工频过电压值密切相关。从工频过电压的研究结果可知，发生单相接地时，健全相电压的升高系数K与系统的X0/X1（从接地点看进去整个系统的零正序阻抗比值）有很大关系，如式（6-3）所示，而系统的X0/X1比值与电源阻抗又有密切联系。显然电源阻抗的X0/X1越大，系统的X0/X1就越大，故健全相电压的升高系数也因此越大，如图6-10所示，从而在此基础上产生的单相接地时的操作过电压也就越大。

图6-10　升高系数K与系统X0/X1比值的关系曲线

（2）单相接地故障过电压与电源正序阻抗的关系

在保持两端电源X0/X1阻抗比均在1.4的情况下，分别改变两端电源E1、E2的正序阻抗X1E1、X1E2，计算该过电压，结果如表6-14所示，表中的过电压值均为该条件下整条线路上不同位置发生接地故障时的最大过电压值。

表6-14　不同电源正序阻抗下单相接地故障过电压的计算结果

由表6-14可知，随着电源正序阻抗从40Ω到180Ω逐渐增加，单相接地故障过电压幅值均呈现先减后增的V型趋势，因而在阻抗范围的边界处，出现了过电压的极大值。分析如下：

一方面，单相接地故障过电压随系统的X0/X1比值的增加而增大，如图6-10所示，而系统的X0/X1与电源X0/X1以及线路X0/X1有关。用X0源表示电源零序阻抗，X1源表示电源正序阻抗，a表示电源零正序阻抗比，用X0线表示输电线路零序阻抗，X1线表示输电线路正序阻抗，b表示输电线路零正序阻抗比，且a＜b，则从故障点看进去整个系统的零正序阻抗比X0系/X1系为

由于特高压线路的零正序阻抗比b在2.6左右，故保持电源零正序阻抗比不变的情况下，由式（6-4）可知，随着电源X0和X1的成比例增加，系统的X0/X1反而减小，由此过电压幅值减小。

另一方面，从操作过电压角度分析，X1的存在相当于等价延长了线路长度，而线路越长过电压就越大，因此，X1越大单相接地故障过电压也就越大。

在这两种因素的共同作用下，当X1较小时，前者因素起主导作用，而X1较大时，后者的影响则较为突出。因此，随着电源X1的增加，过电压幅值呈现了先减小后增大的V型趋势。

（3）求取单相接地故障过电压最大值的方法总结

前面两小节的结论是针对长度为600km的线路所得出的结果，进一步计算表明，当线路长度发生变化时，电源阻抗特性对单相接地故障过电压的影响与该条线路呈现相同的规律，即电源阻抗的零正序阻抗比越大，过电压越大；当电源阻抗的零正序阻抗比保持不变的情形下，过电压随着电源正序阻抗的增加呈现V型变化趋势。因此，对于一般的特高压线路，单相接地故障过电压的最大幅值出现在两端电源X0/X1取最大值且X1取阻抗边界值时的情形。

电源E1、E2的正序阻抗为X1E1、X1E2，其上、下边界值分别为180Ω、40Ω。取特高压等效电源的正序阻抗X1的边界值（即X1上边界、X1下边界）时，有四种情况，分别是（X1E1=X1上边界、X1E2=X1上边界）、（X1E1=X1下边界、X1E2=X1下边界）、（X1E1=X1上边界、X1E2=X1下边界）、（X1E1=X1下边界、X1E2=X1上边界）。在以上每一种电源阻抗取值情形下，充分考虑接地因素的影响，设沿线等间距分布有n个单相接地点，分别求取各个接地点故障时的沿线最大过电压值，n个沿线最大过电压值的最大值即为该种电源阻抗情形下的单相接地故障过电压值。分别计算这四种电源阻抗取值情形下的单相接地故障过电压值U1max、U2max、U3max、U4max，选取四者中的最大值，即为该条线路的单相接地故障过电压最大值Umax。图6-11展示出了求取一定长度特高压线路单相接地故障过电压最大值的步骤。

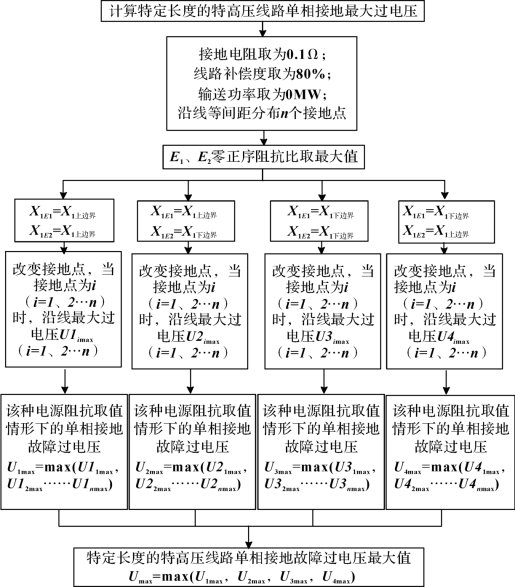
图6-11　求取单相接地故障过电压最大值的步骤

实际上，在大多数情况下，X1E1=40Ω、X1E2=40Ω时，且两端电源的零正序阻抗比均为1.4，单相接地故障过电压幅值最大。所以，有时为方便起见，也可以考虑简单取该种情况对单相接地故障过电压最大值进行直接估算。

综合以上分析，在计算某条线路的单相接地故障过电压最大值时，先将线路输送功率取为0MW、线路补偿度取为80%、接地电阻取为0.1Ω，然后在保证两端电源零正序阻抗比最大的前提下，选取两端电源正序阻抗取边界值的4种运行方式，在4种运行方式下，改变接地点，算取每种运行方式下的单相接地故障过电压，4种运行方式下的单相接地故障过电压值的最大值即为该条线路在两端等效电源取阻抗范围内的任一阻抗值时的单相接地故障过电压最大值。

6.2.3.3　单回线路与双回线路下该过电压的比较

单回模型和双回模型的线路参数分别参考我国晋东南—南阳—荆门特高压单回示范线路和淮—皖—浙—沪特高压双回线路，同时保持两种线路情况下的电源特性、高抗补偿度等参数相同，比较分析单回线路和双回线路的单相接地故障过电压情况。

考虑到双回线路有一回接地（一回运行）和两回运行两种运行模式，下面通过计算分析不同运行方式下的过电压情况，结果如表6-15所示。

表6-15　单回线路/双回线路的单相接地故障过电压比较

由表6-15可知，同种情况下，单回线路的单相接地故障过电压要比双回线路时严重。这是因为同长度下，双回线路系统较单回线路系统联系更紧密而且更稳定，不易引起剧烈的过电压波动。且在相同线路长度下，若回路越多则对过电压波的分散消耗作用就越大，故双回线路过电压幅值较单回线路低[4]。由此可以推论，若单回线路下单相接地故障过电压能得到有效控制，则同样条件下双回线路的该过电压也能被有效控制。