并联电抗器中性点小电抗补偿接与应用

5.2.1.1　单回线路限制原理及小电抗选择

大多数国家超高压线路、特高压线路上考虑采用如图5-2所示的并联电抗器中性点接小电抗来限制潜供电弧，其思想是通过补偿相间电容来限制潜供电流的容性分量。并联电抗器中性点接小电抗后的系统如图5-3（a）所示，假设两侧均为无穷大电源系统，三相电势为和，XLP为高压并联电抗器，简称高抗，XLN为中性点小电抗[1]，Cm1、Cm2为相间电容，M1、M2为相间互感，CD1、CD2为相对地电容。

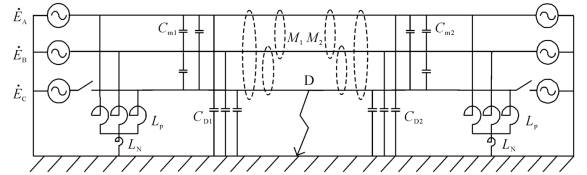
图5-2　并联电抗器中性点接小电抗补偿的线路示意图

加装小电抗的高抗可通过变换得如图5-3（b）所示的电路，相互之间的参数关系如下[1]：

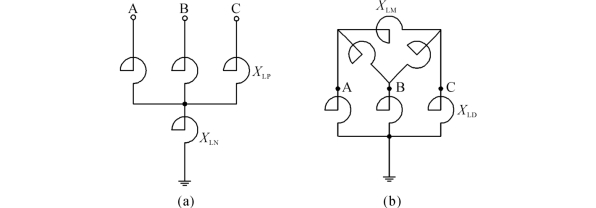
图5-3　并联电抗器加装中性点接小电抗的示意图

式中，XLD和XLM为等效的对地电抗和相间电抗。

通过式（5-1）可知高抗XLP和对地电抗XLD、相间电抗XLM的容量存在以下关系：

式中，U0N为相电压有效值。

由式（5-2）可知，高抗XLP的容量等于对地电抗XLD和相间电抗XLM的容量之和，小电抗并未改变补偿容量，其作用是使高抗的容量被合理分配到相间和对地两部分。

下面对中性点接小电抗限制潜供电流的原理进行分析。小电抗限制潜供电流的原理图如图5-4所示，图中C相发生单相接地故障后，两端单相断路器跳闸，健全的A、B两相通过电容耦合和电感耦合向故障点提供潜供电流，即潜供电流包括容性分量和感性分量两部分。图5-4中1号路径为潜供电流容性分量的流通路径，电流I′1、I″1从健全相经相间电容（Cm1、Cm2）和等效相间电抗（Lm1、Lm2）流至悬空故障相，再经故障点流到地面，I′1+I″1即为流过故障点的潜供电流容性分量。图5-4中2号路径为潜供电流感性分量的流通路径，感性分量由健全相电流通过相间互感M1和M2在故障相上感应出电势，再经过故障相对地电容（CD1、CD2）和等效对地电抗（LD1、LD2）与故障点形成左、右两侧回路，从而在左、右两侧回路中产生环流I′2和I″2，I′2-I″2即为流过故障点的潜供电流感性分量。

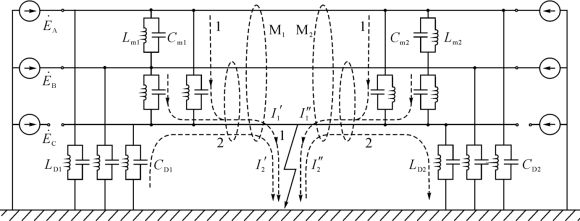
图5-4　并联电抗器中性点接小电抗的线路示意图

单回线路高抗中性点加装小电抗主要是为了限制潜供电流的容性分量，其流通回路如图5-5所示，等值电路图如图5-6所示，其中，CM为总的相间电容（Cm1+Cm2），LM为总的等效相间电抗（Lm1∥Lm2），CD为总的相对地电容（CD1+CD2），LD为总的等效对地电抗（LD1∥LD2）。

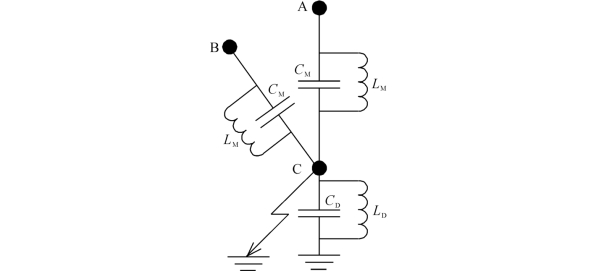
图5-5　并联电抗器中性点接小电抗限制潜供电流原理图

由于弧道电阻Rg远小于等效对地电容CD和对地电抗LD的阻抗，故简化起见，图5-6（b）忽略对地电容和等效对地电抗对弧道电阻上潜供电流的影响。

可以看出，要使弧道流过的潜供电流最小，则需使2CM和LM/2阻抗相等、形成并联谐振。由此可得：

根据全线正、零序电容C1、C0，可计算线路相间电容CM为

则得相间电容的阻抗为

故

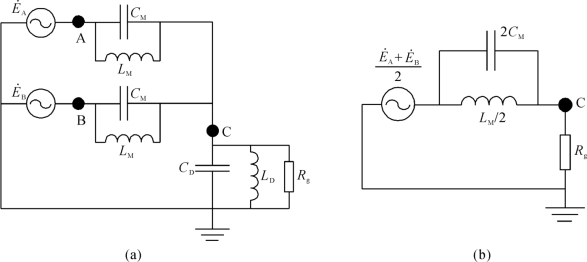
图5-6　并联电抗器中性点接小电抗限制潜供电流等值原理图

设线路补偿度为k，由式（4-13）可得XLP=XC1/k，结合式（5-1）、式（5-4）即可计算出小电抗的最佳阻抗值为

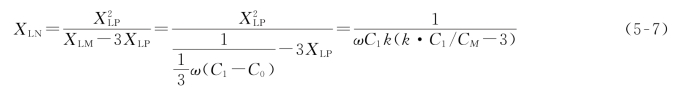
恢复电压的容性分量实际上是由相间阻抗（等效相间电抗与相间电容并联）和故障相对地阻抗（等效对地电抗与故障相对地电容并联）分压形成的，按照式（5-7）选取小电抗后，线路相间形成谐振状态，相间阻抗很大，而相对地电容仅被部分补偿，相对地阻抗相对来说较小，从而使故障相对地阻抗上电压较小，即故障相恢复电压的容性分量较小。而恢复电压中往往是容性分量占主导作用，容性分量被限制会使恢复电压幅值大大降低，从而达到快速熄弧的目的。

同时，由于对地电容也被等效对地电抗部分补偿，潜供电流感性分量回路的阻抗显著增加，而其感应电势并未变化，这样使得潜供电流感性分量的幅值也会有较大的降低。但需要指出的是，中性点小电抗的目的主要是通过完全补偿相间电容限制潜供电流容性分量，虽然等效对地电感对感性分量有一定限制效果，但这不是主要目的。一般不宜通过刻意提高高抗补偿度使对地电容得到更大程度补偿的方式来限制潜供电流感性分量，因为如果补偿度过高，可能会带来谐振的危险。以补偿度为100%为例，小电抗合适时，相间和对地电容均被完全补偿，线路对地电容与等效相对地电抗也形成并联谐振，反而会使恢复电压大幅提升，不利于潜供电弧的熄灭。

5.2.1.2　双回线路限制原理及小电抗选择

采用小电抗限制同塔双回特高压线路潜供电流时，小电抗加装方法与单回线路相同，仍加装在每回线路各组高抗的中性点。但由于同塔双回线路回路之间耦合电容的作用，导致不同运行方式、不同故障类型时潜供电流呈现不同的特性，故其潜供电流的限制比单回特高压线路复杂，主要表现在中性点小电抗阻抗值的选择更为复杂。

根据出现概率，双回线路主要考虑以下两种运行方式：

（1）单回运行方式；

（2）两回运行方式。

不同运行方式时，由于可提供潜供电流的电容不同，补偿这些电容所需的相间电抗也不同，从而导致各个方式下最合适的小电抗阻抗值不同，需综合考虑以确定最终小电抗。在确定小电抗方案之后，也需同时考虑两种运行方式下的谐振情况，确定高抗的上限。

1）单回路运行方式

在线路单回路运行时，另一回一般两端接地。此时线路电容结构如图5-7（a）所示，图中暂不考虑电抗，左边回路的C相为故障相，其两端断路器已跳开，A、B相为带电的健全相，右边回路的a、b、c相接地，电位为0。

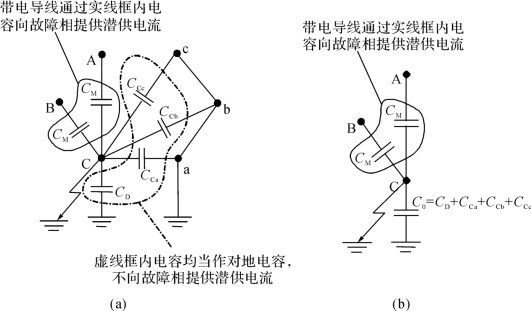
图5-7　单回路运行方式电容示意图

将图5-7（a）简化可得图5-7（b）[2]，可以看出，潜供电流全部由本回相间电容提供。回路之间的电容不仅不会向悬空相提供潜供电流，还会分流部分原应从线路对地电容CD流入地面的潜供电流。故要使单回接地时的单回路运行方式下潜供电流最小，则只需将本回的相间电容完全补偿，情况与单回线路相同。

图5-8为考虑电抗之后潜供电流容性分量流通回路的等值电路。

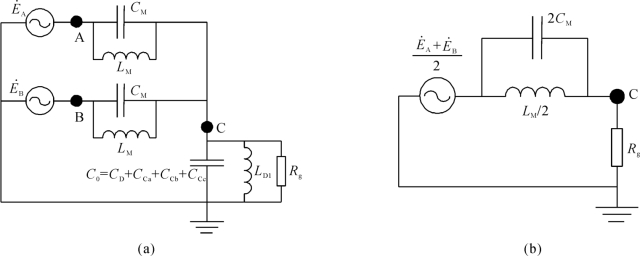
图5-8　单回路运行方式潜供电流容性分量回路示意图

由于弧道电阻Rg远小于等效对地电容C0和对地电抗LD1的阻抗，故简化起见，图5-8（b）忽略等效对地电容和对地电抗对弧道电阻上潜供电流的影响。

可以看出，与单回线路相同，要使潜供电流被限制到最小，要求此时的相间电抗和相间电容的阻抗相等，即

线路补偿度为k，采用与单回线路类似的方法，根据全线正序、零序电容C1、C0，以及高抗计算单回路运行方式下小电抗的理想阻抗值[2]：

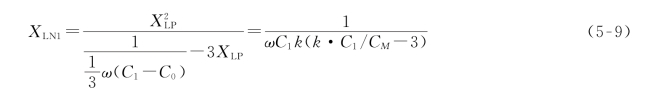
可以看出，实际上，双回线路在单回路运行方式下理想小电抗的求法与单回线路完全一致。

2）两回路运行方式

两回路运行方式电容如图5-9所示，图中暂未考虑电抗，左边回路的C相为故障相，A、B相为带电的健全相，a、b、c相正常工作。

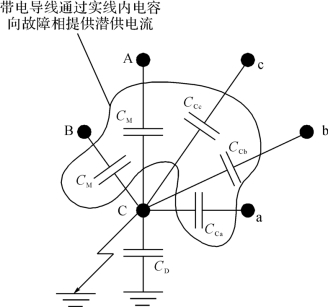
图5-9　两回路运行方式下线路电容示意图

参考第4章的分析，双回线路两回路运行方式下在高抗中性点加装小电抗的电容简化电路如图5-10所示，图5-11为其等值电路图[2]。

从图5-10可以看出，要将潜供电流限制到最低水平，需将A、B两相与C相之间大小分别为CM+（CCa-CCc）和CM+（CCb-CCc）的电容补偿掉。考虑并联高抗和中性点小电抗的作用，等值电路如图5-11（a）所示，图中LM2和LD2分别为考虑高抗和小电抗等值变换得到的等值相间电抗和对地电抗，Rg为弧道电阻。

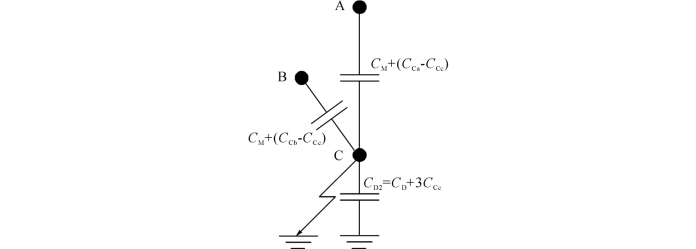
图5-10　双回线路两回路运行方式下的电容简化电路

根据戴维南定理，将图5-11（a）虚线区域内的两并联支路等效为一个电压源串联一个阻抗的形式（如图5-11（b）所示），其中等于图5-11（a）中C点断开时的开路电势；另外，由于弧道电阻Rg远小于等效对地电容CD+3CCc和对地电抗LD2的阻抗，为简化起见，图5-11（b）中忽略等效对地电容和对地电抗对弧道电阻上潜供电流的影响。

从图5-11（b）可知，要使容性潜供电流被完全补偿，则需2CM+（CCa-CCc）+（CCb-CCc）与LM2/2的并联电路并联谐振，此时相间电感的阻抗为

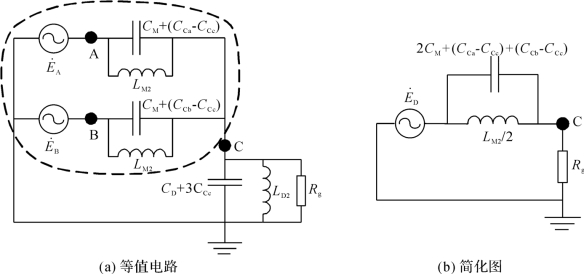
图5-11　考虑并联高抗和中性点小电抗之后的等值电路及其简化图

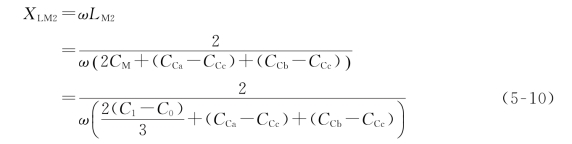
将式（5-10）代入式（5-1），得双回路运行时中性点小电抗的理想值XLN2：

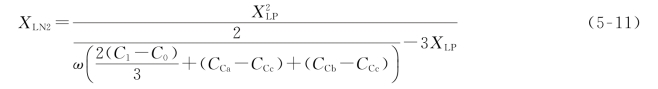
3）最终小电抗选取方法(www.xing528.com)

单回路、两回路两种运行方式下理想小电抗值不同，且两回路运行方式下的理想小电抗的阻抗值一般高于单回路运行方式，即

这是由于要将潜供电流限制到最小，两回路运行方式下相间电抗需同时补偿本回路的相间电容和部分回间电容，而单回路运行方式下相间电抗只需补偿本回路的相间电容，即两回路运行方式下理想相间电抗的阻抗应更小。故根据式（5-1）可知两回路运行方式下的理想小电抗一般高于单回路运行方式。

在得到单回路运行方式和两回路运行方式下理想小电抗XLN1和XLN2之后，需考虑两种运行方式的出现概率，对单、两回路运行方式的理想小电抗进行加权平均来确定最终的小电抗方案。

式中，p1和p2分别为单回路运行方式和两回路运行方式的出现概率，XLN为最终小电抗阻抗值。一般情况下，为充分发挥特高压双回线路的输送能力，线路通常都是两回同时运行，仅在检修等特殊情况下才运行于单回路方式，故p2通常远大于p1。

对于单回路运行方式和两回路运行方式下理想小电抗XLN1和XLN2的求取，目前主要有两种方法，一种是直接分析法，另一种是试探法。

（1）直接分析法

基于上一章和本节前面的详细理论分析，可通过式（5-9）、式（5-11）直接计算出单回路运行方式和两回路运行方式下理想小电抗。再通过式（5-13）采用加权平均得到最终的小电抗值方案。采用该方法的工作量较试探法大幅减少。

（2）试探法

在缺乏对双回线路潜供电流的理论分析的情况下，双回线路通常采用试探法确定中性点小电抗。其方法是在各个方式下，逐个计算不同小电抗时的潜供电流，某方式下潜供电流最小时所对应的小电抗即为该方式下的理想小电抗。

以某长度为400km、全线采用鼓型塔、高抗补偿度为85%的双回特高压线路为例对试探法的具体步骤进行说明。

步骤一：单回运行方式和双回运行方式下，改变小电抗阻抗值，计算各个小电抗阻抗值下的潜供电流幅值，并取三相故障中潜供电流的最大值作出小电抗与潜供电流的关系图，如图5-12所示。

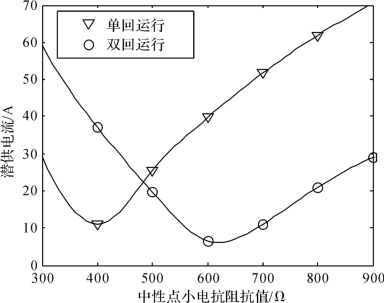
图5-12　试探法结算结果

步骤二：根据图5-12，一回接地时的单回运行方式下，中性点小电抗为400Ω时潜供电流最小；两回运行方式下，中性点小电抗约为600Ω时潜供电流最小。

步骤三：将两者加权平均，将该线路中性点小电抗阻抗值取为500Ω。

此方法的缺点在于，需在各种运行方式下逐个计算不同小电抗阻抗时的潜供电流，计算量非常大。

5.2.1.3　小电抗计算中所需输电线路参数的测量方法[3]

1）线路正序电容C1

测量线路正序电容C1时按照图5-13接线。线路末端开路，首端加三相电源，在始端测量三相的电流，两端均测量三相电压，并测量三相功率。双回线路测量正序电容时另一回应两端三相接地，以减小其对测量结果的影响。

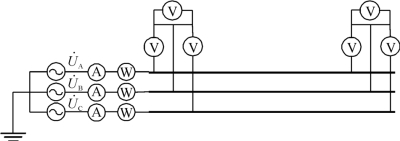
图5-13　测量正序电容接线图

每相导线正序参数按下式求得：

单位长度正序导纳：

单位长度正序电导：

单位长度正序电纳：

单位长度正序电容：

全线正序电容：

式中，P1为三相损耗总功率（MW），Uav1为首末端三相线电压平均值（有效值，kV），Iav1为三相电流平均值（有效值，kA），l为线路长度（km），f为电源频率（Hz）。

2）线路零序电容C0

测量线路零序电容C0时按照图5-14接线。线路末端开路，始端三相短路施加单相电源，在始端测量三相零序电流之和，并测量始末端电压的平均值，此外测量三相零序总功率。双回线路测量零序电容时，另一回应两端三相接地，以减小其对测量结果的影响。

图5-14　测量零序电容接线图

每相导线零序参数按下式求得：

单位长度零序导纳：

单位长度零序电导：

单位长度零序电纳：

单位长度零序电容：

全线零序电容：

式中，P0为三相零序损耗总功率（MW），Uav0为首末端相电压平均值（有效值，kV），I0为三相总零序电流（有效值，kA），l为线路长度（km），f为电源频率（Hz）。

3）双回线路回间耦合电容

在计算双回线路中性点小电抗时，需要知道双回线路回路间的电容参数。测量不同回路两相间耦合电容时按照图5-15接线（以测量A相和c相之间电容为例），将回路I的一相接电压源，测量回路II的一相通过电流表接地，其他四相接地。

图5-15　测量回间电容接线图

按下式计算不同回路的两相导线间电容：

式中，I为电流表测量的电流，U为所加电压，f为电源频率。

5.2.1.4　限制要求

单相重合闸时间定义为从系统发生故障，线路保护装置发生反应到完成重合闸操作的时间，主要包括保护和开关动作时间、弧道游离和恢复时间、及潜供电弧持续时间（或自熄灭时间）。对于高抗补偿线路，其分布过程如图5-16所示。在超/特高压系统中，单相重合闸时间一般取1s，由此可推算出接地点潜供电弧的自熄灭时间大约在0.67s以内，只有这样才能满足1s单相重合闸的要求。

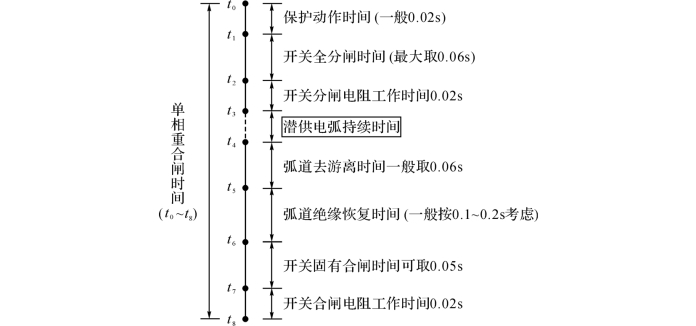
图5-16　高抗补偿线路单相重合闸时间分布过程示意图

华北电力科学研究院对潜供电弧自灭特性进行了大量试验研究，得到了风速大于1.5m/s、起弧电位梯度低于13.5kV/m、有高抗补偿时，潜供电弧熄灭概率为90%情况下熄灭时间t与潜供电流大小IC的拟合公式[4]：

由式（5-25）可得：潜供电流幅值为35A（有效值）的潜供电弧自灭时间（概率90%）是0.71s。因此，对于有高抗补偿的线路，当采用1s左右的重合闸时间时，单相重合闸过程中的潜供电流值应控制在35A以内。

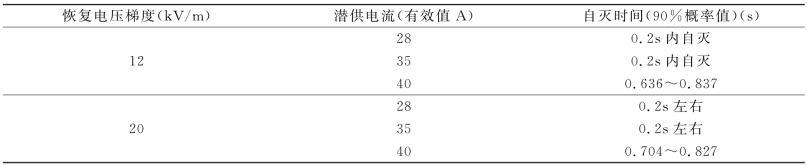
为满足特高压工程建设，中国电力科学研究院进一步对正常补偿线路进行了潜供电弧的自灭特性研究。对于有高抗补偿的线路，风速在1.5～2.0m/s范围内时，恢复电压梯度分别为12kV/m和20kV/m时，不同潜供电流下的潜供电弧自灭时限推荐值如表5-1所示[5]。

从表5-1可以看出，正常补偿时，恢复电压梯度20kV/m及以下，潜供电流35A及以下时，均能在0.2s左右快速自灭，潜供电流40A时，潜供电弧自灭时间增大到0.7s左右。中国电科院认为，潜供电流35A至40A之间存在某一值，其潜供电弧及其自灭时间有迅速增大的现象。综合以上两研究单位的研究结果可知，对于采用高抗中性点加装小电抗的线路，为满足1s重合闸时间的要求，潜供电流有效值应被限制至35A及以下。

表5-1　正常补偿下潜供电弧自灭时间推荐值