确定高抗补偿度的上限值

4.7.1.1　单回特高压线路高抗补偿度上限研究

高抗是特高压电网中的重要电气设备，它可较好地补偿线路中的动态容性无功，有效地抑制工频过电压。但是，装设高抗作为线路无功补偿设备，使系统增加了发生谐振的可能性。实际上，如果并联高抗采用中性点直接接地方式（即中性点不通过小电抗接地）进行补偿，则并联高抗可能会在非全相投切的线路中引发工频谐振现象。而采取在高抗中性点加装小电抗的方式，如果小电抗值选择合适，可较好地阻隔输电线路的相间联系，明显减小了非全相运行中“健全相”对“故障相”的影响，从而有效地抑制工频谐振过电压的发生。但中性点小电抗的设计值与实际值往往会有一定的偏差，系统的频率也往往与50Hz的基准频率之间有一些偏差，这些因素导致了在并联高抗补偿度太高的情况下会存在系统发生工频谐振的可能性。因此，有必要对并联高抗补偿度上限的问题展开详细研究，以避免系统发生工频谐振。

1）非全相运行谐振过电压产生机理

非全相运行谐振过电压是由于线路一相因故障跳开悬空后，线路健全相通过相间电容及高抗与之形成谐振回路而产生的[16-17]。图4-42为非全相运行示意图，其中，假设两侧均为无穷大电源系统，三相电势分别为为相间电容；CD为各相对地电容；LP为高抗；LN为高抗中性点接地电抗，即俗称的“小电抗”。故障开断C相线路又称“悬空相”，A相、B相线路称“健全相”。

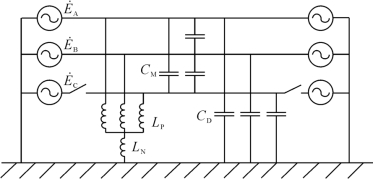
图4-42　非全相运行示意图

为限制潜供电流，高抗中性点加装一个小电抗XLN。此时，高抗的补偿容量分至相间电抗和对地电抗，其中XLM为等效相间电抗，XLD为等效对地电抗，如图4-43所示。

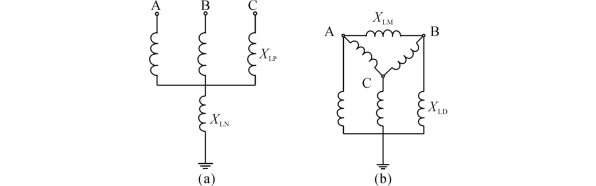
图4-43　并联电抗器中性点接小电抗的等值示意图

图4-43（a）与图4-43（b）之间的参数对应关系如下：

图4-42经过变换后可得图4-44所示电路。由于A相与B相对地电容及这两相之间的相间电容直接接在健全相电源上，故不予以考虑，由此得等值电路如图4-45（a），再进一步简化，将A、B相合并可得图4-45（b）所示的等值电路，其中C点电位为悬空的C相电位。

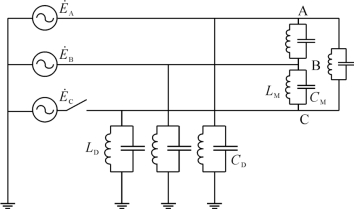
图4-44　非全相运行线路等效电路图

根据图4-45（b）所示电路，断开相电压UC为

图4-45　非全相运行线路简化图

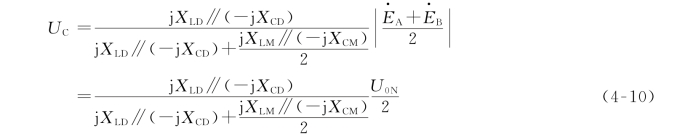
式中，U0N为相电压有效值；。

在一定的高抗及小电抗参数配合下，若相间阻抗和对地阻抗XLD∥XCD满足串联谐振条件

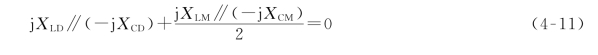
或

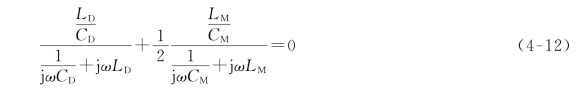
则相间阻抗和对地阻抗发生串联谐振，会在悬空的C相产生幅值很高的谐振过电压（即UC→∞）。

2）发生谐振过电压的原因

理论上，若按照相间完全补偿的原则来选择中性点小电抗时，任何高抗补偿度下都不会产生高幅值的非全相运行谐振过电压（即）。但由于设备的实际参数与其设计参数往往存在一定差别，仍有可能产生发生谐振过电压的风险。具体原因如下：

（1）小电抗阻抗值的偏差

小电抗阻抗值偏差会使高抗补偿容量分配出现误差，这可能导致线路谐振。

（2）频率偏差

线路高抗及小电抗的配置均是按工频50Hz得出的，但故障时系统频率往往偏离工频50Hz，这可能会使线路在非全相运行时产生谐振过电压。

3）发生谐振过电压的条件

（1）小电抗阻抗值偏差

此处重点研究小电抗阻抗值偏差导致的谐振过电压条件，假设频率为工频并保持不变。

要使图4-45（b）中电路发生串联谐振，则串联的两部分必须分别为容性和感性，若同为容性或同为感性，则不可能发生串联谐振。所以，只有两种条件下才可能发生非全相运行谐振过电压：相间过补偿、对地欠补偿；或者相间欠补偿、对地过补偿。

以下研究分两步进行。首先研究实际中发生这两种情况的可能性；然后给出各高抗补偿度下谐振过电压与小电抗阻抗值偏差的关系。

高抗补偿度k是工频下高抗补偿容量与线路正序电容无功功率的百分比，具体为

式中，U0N为相电压；XLP为高抗阻抗；XC1为线路正序电容的阻抗值，XC1=3XCM+XCD。

（a）小电抗阻抗值偏差来源及最大偏差程度分析

特高压线路设计中，小电抗阻抗值确定过程如下：

①通过特高压线路杆塔、导线的几何参数建模计算出线路的序参数。

②以工频过电压限制为依据确定高抗补偿容量，并向高抗生产厂家订货。

③通过高抗设计值（此时高抗尚未交付，无法得到高抗实际参数）和线路理论计算参数（此时线路尚未完工，无法得到线路实际参数）得出小电抗阻抗值，该值定义为小电抗阻抗的设计值，并向小电抗生产厂家订货。

④小电抗交付之后，通过线路、高抗及小电抗的实际参数，确定小电抗分接头接法。

将第④步中小电抗交付时的阻抗值称为成品小电抗的阻抗值。对于任意一条已经完工的线路，都存在一个能将其潜供电流限制到最小的小电抗阻抗最优值，简称小电抗的实际所需值。

谐振研究的是实际线路上的谐振过电压，所以要考虑的小电抗偏差是指成品小电抗阻抗值与小电抗的实际所需值之间的偏差，用P表示。由小电抗的设计和制造过程可知，小电抗阻抗值的偏差源于如图4-46所示的两方面原因：

①在设计小电抗阻抗值时，由于线路尚未完工，只能以理论计算的线路参数和高抗参数计算小电抗阻抗值，而实际线路参数和高抗参数往往与理论计算参数会存在一定的差异，从而使小电抗阻抗值的设计值与实际所需值之间存在偏差。此类偏差称为设计偏差，即图4-46中的P1，设小电抗阻抗设计值大于实际所需值时，P1＞0，反之，则P1＜0。

②小电抗制造过程中产生的阻抗值偏差，即小电抗阻抗的设计值与成品小电抗阻抗值之间的偏差。此类偏差称为制造偏差，即图4-46中的P2，设成品小电抗阻抗值大于设计值时，P2＞0，反之，则P2＜0。

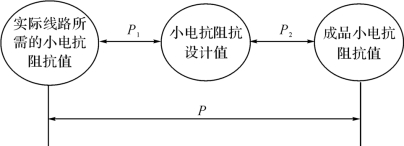
图4-46　小电抗阻抗值偏差关系图

注：以理论计算小电抗阻抗值为基准

谐振研究中应考虑P可能存在的最大值。从严取值，考虑线路参数和高抗参数的理论计算值与实际测量值的偏差，通常P1不会超过±15%（各偏差的百分数以设计值为基准）；考虑中性点小电抗的制造偏差，通常P2不会超过±5%（基于目前供货厂商的制造能力，中性点小电抗器的制造误差一般控制在±5%）。综上所述，考虑最严重情况，以理论计算小电抗阻抗设计值为基准，成品小电抗阻抗值取-5%偏差，线路实际需要的阻抗值取+15%偏差，则成品小电抗阻抗值与实际线路所需的小电抗阻抗值之间的偏差P不会超过20%。考虑到特高压中性点小电抗一般还设有2个抽头，其阻抗调整范围为额定阻抗的±10%，若选择+10%抽头，则从严考虑小电抗偏差P最大值也不会超过10%。图4-47给出了小电抗最大负偏差的计算图（考虑抽头后，成品小电抗与线路实际需要的阻抗值之间的最大负偏差为-10%）。

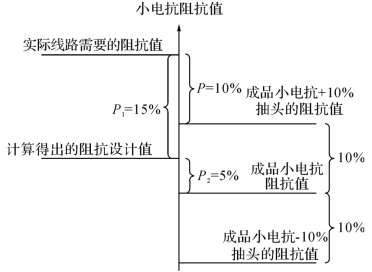
图4-47　小电抗最大负偏差计算图

注：以理论计算小电抗阻抗值为基准

（b）小电抗阻抗值偏差引起谐振过电压的分析

设加装高抗后，线路两相之间的阻抗为XM，线路每相对地的阻抗为XD，XM和XD的无功功率分别为QM和QD，假设感性无功为正，则有

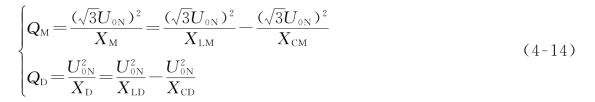
若相间电容欠补偿，则XM为容性、QM＜0；相间电容过补偿，则XM为感性、QM＞0。若对地电容欠补偿，则XD为容性、QD＜0；对地电容过补偿，则XD为感性、QD＞0。

先将图4-45（a）简化为图4-48（a），然后将A、B两相合并，得到图4-48（b）所示的等值电路。

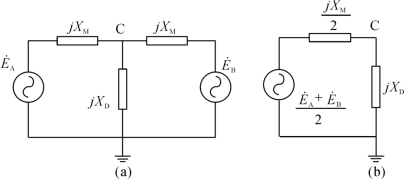
图4-48　线路非全相运行阻抗

根据图4-48（b）可得C相上电压为

由式（4-14），令比值

将式（4-16）代入式（4-15），则C相上过电压幅值为

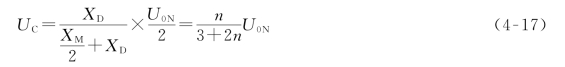
根据式（4-17）作出断开相电压与比值n之间的关系曲线，如图4-49所示。

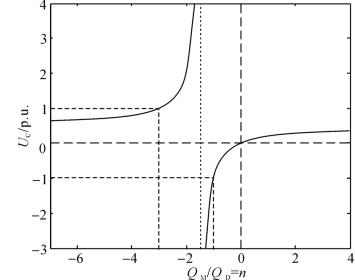
图4-49　断开相电压与n的关系

相间补偿和对地补偿这两者中，当一者为欠补偿、另一者为过补偿时，n为负；当二者均为欠补偿或过补偿时，n为正。当n在区间（-∞，-3）及（-1，+∞）中时，悬空的C相电压低于正常运行电压。n在（-3，-1）区间时，悬空的C相电压已经超过了正常工作电压，其中，n=-1.5时，相间与对地阻抗发生完全谐振（0.5XM+XD=0），此时理论上过电压幅值将趋向无穷大。

（c）小电抗阻抗值偏差与谐振电压幅值的关系

由式（4-9）、（4-10）、（4-12）、（4-13）可计算三种高抗补偿度下，小电抗阻抗值偏差与过电压幅值之间的关系，结果见图4-50。

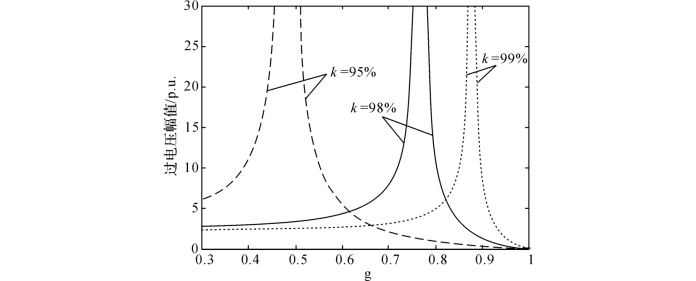
图4-50　不同高抗补偿度下悬空相（C相）谐振过电压幅值与小电抗阻抗值偏差系数g的关系

由图4-50可见，当小电抗阻抗值为理想值时（相间电容完全补偿，g=1），悬空相电压为0；随着小电抗阻抗值逐渐减小，悬空相上电压逐渐增大；当小电抗阻抗值为小于理想值的某一特定值时，悬空相上的谐振过电压可达无穷大。在实际中即使不出现谐振过电压为无穷大的完全谐振情况，所产生的谐振过电压也足以危害设备安全。

（d）不同高抗补偿度下导致谐振的小电抗阻抗值偏差

改变高抗补偿度k的大小，计算不同高抗补偿度下，导致谐振发生的小电抗阻抗值偏差。

图4-51为不同高抗补偿度下发生谐振时所对应的小电抗阻抗值偏差。图4-51中，横坐标为线路高抗补偿度，纵坐标表示产生谐振过电压时小电抗阻抗值比实际所需值偏小的百分数。

由图4-51可见，高抗补偿度越接近100%，导致谐振发生的小电抗阻抗值偏差越小，即越容易发生谐振。故为避免谐振过电压的产生，应避免高抗补偿度过于接近100%。

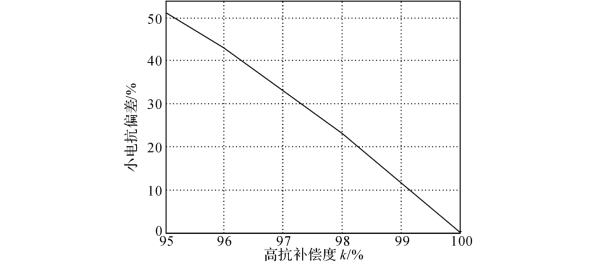
图4-51　不同高抗补偿度下发生谐振时对应的小电抗阻抗值偏差

（2）频率偏差

系统发生故障时，系统频率往往会发生一定的变化，这可能导致谐振过电压。

（a）系统频率偏差与谐振电压

利用图4-45（b）进行分析。考虑高抗补偿度小于100%的情况，小电抗按使相间电容完全补偿的原则配置，此时对地电容欠补偿，即有

式中，fn为50Hz。

在某些故障情况下，频率会下降至fg＜50Hz，这将使相间电抗补偿容量增大，相间电容的无功功率减小，从而可能出现相间电容过补偿、对地电容欠补偿的情况，如式（4-19）所示，此时有可能发生谐振；而在频率大于50Hz时，相间和对地都处于欠补偿状态，不会发生谐振。

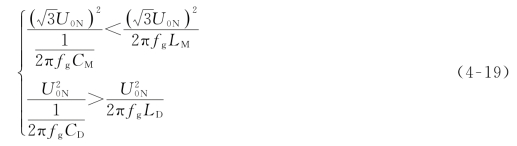
（b）系统频率与谐振过电压幅值的关系

由式（4-9）、（4-10）、（4-12）、（4-13）可计算三种高抗补偿度下，不同系统频率时悬空相C相上的电压，结果见图4-52。

由图4-52可见，当系统频率为工频时，悬空相C相电压很小，随着系统频率的减小，悬空相C相上电压幅值逐渐增大，当系统频率为低于工频（fs＜50Hz）的某一特定值时，悬空相上C相可出现幅值很高的谐振过电压，且出现谐振过电压时的系统频率与高抗补偿度有关。

图4-52　不同高抗补偿度下悬空相C相谐振过电压与系统频率fs的关系

（c）不同高抗补偿度下的谐振频率

根据式（4-4）计算发生谐振时的频率，并改变k的大小，计算不同高抗补偿度下的谐振频率，结果如图4-53所示。图4-53中横坐标为线路高抗补偿度k，纵坐标为产生谐振过电压时的系统频率。

可以根据高抗补偿度在图4-53上查出线路发生谐振时的系统频率。总体而言，高抗补偿度越接近100%，发生谐振时的频率越接近工频，即越容易发生谐振。故为避免谐振过电压的产生，应避免高抗补偿度过于接近100%。

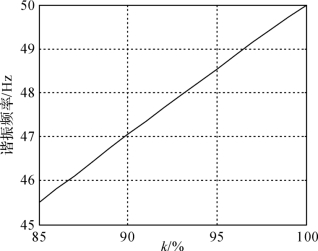
图4-53　不同高抗补偿度下的谐振频率

4）单回特高压线路高抗补偿度上限的确定

在实际系统中，谐振过电压可能由小电抗阻抗值偏差和系统频率波动两个因素共同引起，需对这两者予以综合考虑。

由上文分析可知，为避免发生谐振过电压，高抗补偿度应避免过于接近100%。高抗补偿度最高可达多少，主要取决于小电抗阻抗值和频率这两者的可能偏差程度，在已知或可预估小电抗阻抗值及系统频率可能存在的最大偏差时，可通过该偏差的大小来确定合适的高抗补偿度最大值。

（1）方法

具体步骤如下：

①计算线路各序参数，得到线路相间电容CM和相对地电容CD；又由线路设计要求的高抗补偿度k，由式（4-13）计算得到线路高抗LP。

②由式（4-9）计算工频下相间电容完全补偿时（XLM=XCM）的小电抗阻抗值设计值XLN。

③推导工频下调整抽头后的成品小电抗阻抗值与线路实际所需小电抗阻抗值之间可能存在的最大偏差，令偏差最大时的小电抗电感值为XLNs，通常考虑最大负偏差，为-10%。(www.xing528.com)

④结合线路参数，计算小电抗偏差最大时相间电抗XLMs和对地电抗XLDs（工频下），并进一步计算对应的相间电感LMs以及对地电感LDs，然后将LMs和LDs代入式（4-11）计算图4-45（b）所示的线路回路发生谐振时的频率；改变高抗补偿度k。

⑤计算各高抗补偿度下的谐振频率，作出高抗补偿度k（横坐标）与谐振频率（纵坐标）的关系图。

⑥根据谐振频率要求（小于某值），从上述高抗补偿度k与谐振频率的关系图得出高抗补偿度的上限。

（2）计算实例

考虑成品小电抗阻抗值比线路实际所需值小10%的极端情况，计算单回特高压线路在各高抗补偿度下发生谐振的频率，计算对具有典型呼高的猫头塔和酒杯塔进行，结果如图4-54所示。

根据图4-54，得出典型频率下，考虑小电抗阻抗值偏差及高抗偏差时，发生完全谐振所对应的高抗补偿度，如表4-7所示。

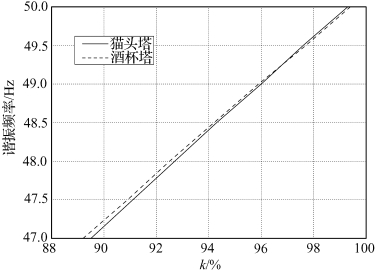
图4-54　不同高抗补偿度下的谐振频率

表4-7　单回特高压线路高抗补偿度与谐振频率之间的关系

对于系统频率波动，国家标准GB/T15945-1995《电能质量电力系统频率允许偏差》[18]规定电力系统正常频率偏差允许值为0.2Hz，当系统容量较小时，偏差值可以放宽到0.5Hz。对于故障频率，各省调度规程多有如下规定：超过50±0.2Hz，持续时间不超过60min；超过50±1.0Hz，持续时间不超过15min；在任何情况下，系统频率不允许超过50±3Hz。同时电力行业标准DL/T428-2010《电力系统自动低频减负荷技术规定》[19]中规定：“其他一般情况下，为了保证火电厂的继续安全运行，应限制频率低于47.0Hz的时间不超过0.5s，以避免事故进一步恶化”。

综合上述，系统频率应很少低于49Hz，考虑适当裕度，此时，对应的高抗补偿度设计上限可取95%；另外考虑系统频率肯定不会低于47Hz，即高抗补偿度大于89%时，肯定不会发生谐振。

因此，对于单回线路，通常情况下，高抗补偿度设计上限一般可选不超过95%；考虑最严酷的情况，高抗补偿度设计上限宜选90%。

4.7.1.2　双回线路高抗补偿度上限研究

对双回线路，本文考虑单回运行和双回运行这两种运行方式。不同运行方式时，由于可提供潜供电流的电容不同，补偿这些电容所需的相间电抗也不同，从而导致各个方式下最合适的小电抗阻抗值不同，需在二者之间综合考虑以确定比较合理的最终小电抗。在确定小电抗方案之后，再同时考虑两种运行方式下的谐振情况，确定高抗的上限。

1）双回线路小电抗阻抗值的计算

（1）单回路运行方式

在线路单回路运行时，另一回一般两端接地。此时潜供电流原理如图4-55（a）所示，图4-55（a）中左边回路的C相为故障相，其两端断路器已跳开，A、B相为带电的健全相，右边回路的a、b、c相接地，电位为0。其中，CCa、CCb、CCc为故障相C对另一回停运线路a、b、c三相之间的回间耦合电容，CM为A、B两相健全相与C相故障相之间的相间耦合电容。

将图4-55（a）简化可得图4-55（b），由此图可见，潜供电流全部由本回相间电容提供。回路之间的电容不仅不会向悬空相提供潜供电流，还会分流部分原应从线路对地电容CD流入地面的潜供电流。故要使单回接地时的单回路运行方式下潜供电流最小，则只需将本回的相间电容完全补偿。即要求此时的相间电抗和相间电容的阻抗相等：

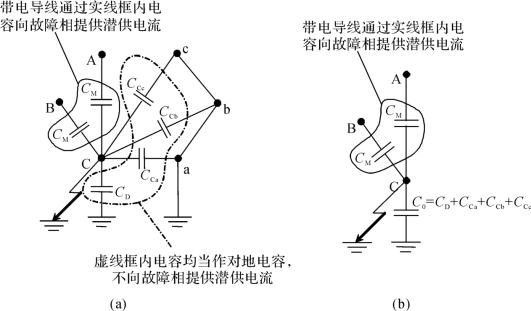
图4-55　单回路运行方式电容分布示意图

根据全线正、零序电容C1、C0，可求得线路相间电容CM为

相应地，相间电容的阻抗为

故由式（4-20），有

将式（4-23）代入式（4-9），得单回路运行方式下小电抗的理想阻抗值为

实际上，双回线路在单回路运行方式下的小电抗理想阻抗值的求法与单回线路完全一致。

（2）双回路运行方式

双回路运行方式下的电容分布示意图见图4-56。图中左边回路的C相为故障相，A、B相为带电的健全相；右边回路的a、b、c相正常工作。

从图4-56可见，与单回路运行方式相比，双回路运行方式时，回间耦合电容CCc、CCb、CCa也会向故障相提供潜供电流。

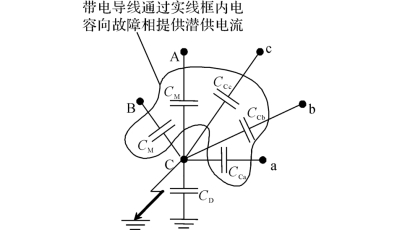
图4-56　双回路运行方式下线路电容分布示意图

虽然线路换位使每回线路三相电压对称，但目前中国双回特高压线路采用如图4-57所示的逆相序换位方式，致使回间耦合电容CCc、CCb、CCa不相等，三相之间不对称，导致a、b、c三相向悬空的C相提供的总电流不为0，使得相间电抗不仅要补偿本回线路的相间电容，还需补偿回路间的耦合电容。

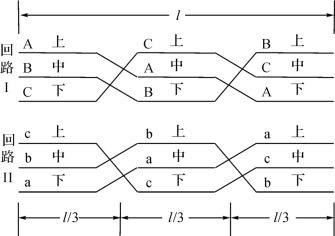
图4-57　逆相序反向换位示意图

下面研究逆相序换位时，相邻回路与故障相之间耦合电容大小。首先将导线按图4-58编号。

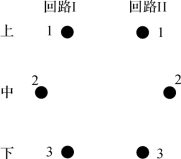
图4-58　导线编号

设图4-58中不同回路的两导线间电容为c11、c12、c13、c21、c22、c23、c31、c32、c33，单位为μF/km。显然，c12=c21，c13=c31，c23=c32。结合图4-57和图4-58可得回路间各相导线间的电容如表4-8所示，表4-8中l为线路长度。

表4-8　不同回路间各相导线间的电容

由表4-8可见，任意一相导线与另一回三相导线之间的电容均不等。且同名相之间的电容均为（c13+c22+c31）l/3，异名相之间两个电容均分别为（c12+c21+c33）l/3和（c11+c23+c32）l/3。

一般情况下，导线之间电容与其间距成反比关系，所以由双回线路的导线分布可得出回间电容之间的关系为

故有

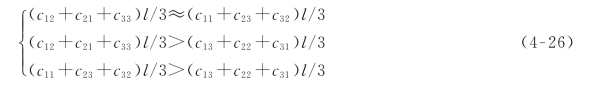
即异名相之间两个电容大小比较接近，且均大于同名相之间的电容。对中国在建的某特高压双回线路进行计算，其C相与a相、b相、c相间电容分别为9.94×10-4μF/km、10.41×10-4μF/km和5.80×10-4μF/km。

对图4-59中各电容进行简化：

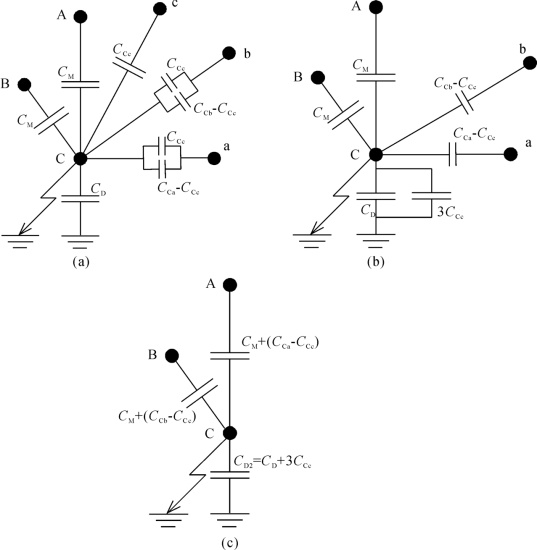
图4-59　回路间电容的化简

①首先将图4-59（a）所示的异名相之间的电容CCa和CCb分别分解为两部分，其中一部分等于同名相之间电容CCc。此时a、b、c相与C相之间各有一个大小为CCc的电容，将这三个含CCc的支路合并。由于三支路的电源电压三相对称，合并后的电源电压为0，故可将这三个CCc电容直接移至C相与地之间，得图4-59（b）所示电路。

②由于A相与a相、B相与b相的电压基本相同，故将a相与C相之间、b相与C相之间剩余的电容CCa-CCc和CCb-CCc分别移至A相与C相之间及B相与C相之间，与相间电容合并，得图4-59（c）所示电路。

从图4-59（c）可见，要将潜供电流限制到最低水平，需将A、B两相与C相之间大小分别为CM+（CCa-CCc）和CM+（CCb-CCc）电容补偿掉。在图4-59（c）所示的电路中加入电抗进行研究，如图4-60（a）所示，图中LM2和LD2分别为等值相间电感和对地电感，Rg为弧道电阻。

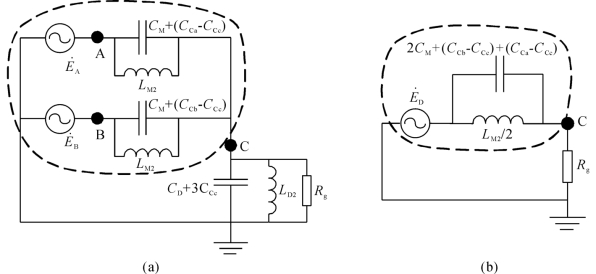
图4-60　考虑电抗之后的电路化简

由于弧道电阻Rg远小于等效对地电容CD+3CCc和对地电感LD2的阻抗，故简化起见，忽略等效对地电容和对地电感对弧道电阻上潜供电流的影响。同时，根据戴维南定理，将图4-60（a）虚线区域内的两并联支路等效为一个电压源串联一个阻抗的形式，如图4-60（b）所示，其中等于图4-60（a）中C点断开时的开路电势。

由图4-60（b）可知，要使容性潜供电流被完全补偿，则需2CM+（CCa-CCc）+（CCb-CCc）与LM2/2的并联电路并联谐振，此时相间电感的阻抗为

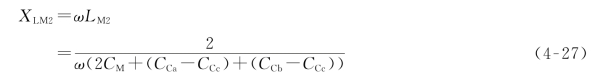
将式（4-27）代入式（4-9），得双回路运行时中性点小电抗阻抗的理想值XLN2为

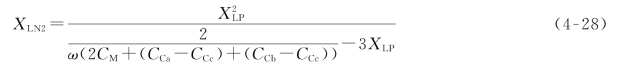
（3）最终小电抗选取

单回路、双回路两种运行方式下小电抗的理想阻抗值不同，且双回路运行方式下小电抗的理想阻抗值一般高于单回路运行方式，即

这是由于要将潜供电流限制到最小，双回路运行方式下相间电抗需同时补偿本回路的相间电容和部分回间电容，而单回路运行方式下相间电抗只需补偿本回路的相间电容，即双回路运行方式下理想相间电抗的阻抗应更小。故根据式（4-9）可知，双回路运行方式下小电抗的理想阻抗值一般要高于单回路运行方式。

在求出单回路运行方式和双回路运行方式下小电抗的理想阻抗值之后，需考虑两种运行方式的出现概率，对单、双回路运行方式下小电抗的理想阻抗值进行加权平均来确定最终的小电抗阻抗值。具体为

式中，p1和p2分别为单回路运行方式和双回路运行方式的出现概率，XLN为最终小电抗阻抗值。一般情况下，为充分发挥特高压双回线路的输送能力，线路一般双回同时运行，仅在检修等特殊情况下才运行于单回路方式，故p2通常远大于p1。

2）双回线路高抗补偿度上限的确定

（1）双回线路高抗补偿度上限计算

研究双回线路谐振时仍考虑以下三种引发谐振的因素：①小电抗的阻抗低于该方式下小电抗的理想阻抗值；②系统频率低于工频50Hz；③高抗补偿度接近100%。

双回线路在单、双回路运行方式下高抗补偿度上限的研究方法与单回线路完全一样，只是谐振回路不同。根据上文中双回线路小电抗阻抗值计算中的分析可知，双回线路在单、双回路运行方式下的谐振回路如图4-61所示。

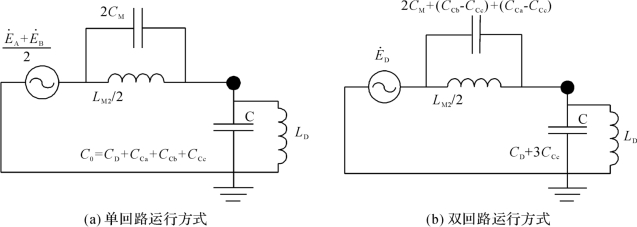
图4-61　双回线路谐振回路

在确定了谐振回路之后，双回线路高抗补偿度上限确定方法与单回线路完全相同。

对中国特高压双回线路所使用的鼓型塔进行计算，得出在考虑小电抗阻抗值偏差时，单、双回运行方式下高抗补偿度与谐振频率的关系，如图4-62所示。

根据图4-62所示的曲线，得出在考虑小电抗阻抗值偏差、高抗偏差的前提下，典型频率下发生完全谐振所对应的高抗补偿度，如表4-9所示。

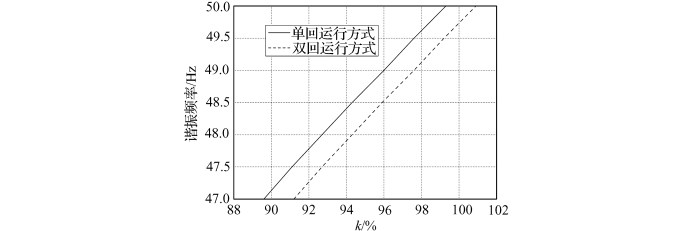
图4-62　　双回线路高抗补偿度与谐振频率的关系

由表4-9可知，对应于某一特定谐振频率，双回线路运行于单回方式所允许的高抗补偿度上限要略低于双回路运行方式。例如，对于谐振频率为48Hz的情况，双回路线路以单回路方式运行时所允许的高抗补偿度上限为90.1%，而以双回路方式运行时所允许的高抗补偿度上限为91.7%，因此，实际中应以双回线路处于单回路运行方式下的情况为依据确定双回线路高抗补偿度上限。参照前文的分析，由于系统频率极少低于49Hz，此时，设计高抗补偿度上限可选取为不超过95%；同时考虑系统频率在任何情况下肯定不能低于47Hz，即设计高抗补偿度低于89%时，肯定不会发生谐振。

表4-9　高抗补偿度与谐振频率对应关系

因此，对于双回线路，通常情况下，高抗补偿度设计上限可选不超过95%；考虑最严酷的情况，高抗补偿度设计上限宜选90%。

（2）双回线路高抗补偿度上限计算结果分析

从图4-62中可以看出，双回路运行时的高抗补偿度—谐振频率曲线位于单回路曲线下方，即相同高抗补偿度下，单回路运行方式下的谐振频率更高，亦即单回路运行时更容易发生谐振。这是由于线路单回路运行方式和双回路运行方式下充电功率不同导致的。

从图4-56中可以看出，单回路运行方式下，回间耦合电容CCc、CCb、CCa均为对地电容，此时其相间电容和对地电容分别为CM和CD+CCa+CCb+CCc，故充电功率为

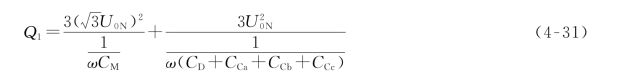
线路双回路运行时，由图4-59可见，等效对地电容变为CD+3CCc，两端加相电压；本回路相间电容CM和异名相之间部分大小为（CCa-CCc）+（CCb-CCc）的电容两端所加的电压为线电压。此时充电功率为

即从单回路运行方式到双回路运行方式时，有大小为（CCa-CCc）+（CCb-CCc）的回间电容其两端电压从相电压转化为线电压，故在总电容相同的情况下，双回路运行方式下的充电功率大于单回路运行方式下充电功率。以典型的鼓型塔为例，其双回运行方式下充电功率约为单回运行方式（每百公里547Mvar）下的1.03倍，达每百公里563Mvar。即在单回运行方式下，高抗补偿的无功充电功率的比例更大，实际高抗补偿度更高，更容易发生谐振。

4.7.1.3　高抗补偿度上限的通用性研究以及单、双回线路高抗补偿度上限的比较

上文的分析计算均以典型参数为基础，得出的结论是否具有通用性尚需验证，故本节将对线路参数变化对高抗补偿度上限的影响进行研究。

规程规定，单、双回特高压线路导线最低距离分别为19m和18m（人烟稀少的非农业耕作区），考虑单回线路弧垂20m，再加上绝缘子和金具的长度12.5m，单、双回线路最低呼高分别为51.5m和50.5m。同时由于呼高过大、杆塔过高会使线路成本增大，一般不会超过70m，故本文考虑呼高在50～70m范围内变化的情况，其电容参数如表4-10及表4-11所示。

表4-10　单回线路参数

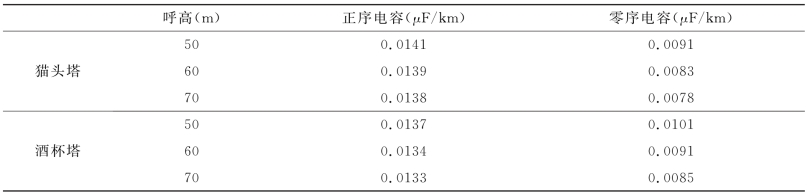
表4-11　双回线路参数

在不同线路参数下，考虑小电抗阻抗值偏差、高抗偏差，单回线路高抗补偿度与谐振频率关系如表4-12所示，双回线路高抗补偿度与谐振频率关系如表4-13和表4-14所示。

表4-12　单回线路高抗补偿度与谐振频率对应关系

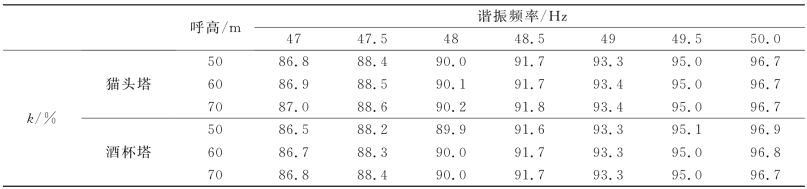
从表4-12、表4-13和表4-14可见，参数变化对单、双回线路谐振频率的影响非常小，从而对高抗补偿度上限影响也非常小，故前面得出的上限适用于通常的各种特高压线路参数。

表4-13　单回路运行方式下双回线路高抗补偿度与谐振频率对应关系

表4-14　双回路运行方式下双回线路高抗补偿度与谐振频率对应关系

双回线路高抗补偿度上限主要从单回运行方式考虑，对比表4-12和表4-13，可见单、双回线路的高抗补偿度上限极为接近。这是由于双回线路在单回路运行方式下，其高抗补偿度上限的确定方法与单回线路完全一致。而从单回线路高抗补偿度上限分析可知，线路参数变化对高抗补偿度上限的影响很小，甚至可忽略不计，导致单、双回线路高抗补偿度上限基本相同。