如何用内点法求解不等式约束最优化问题？

内点法就是要求在可行域内完成迭代。为保证在可行域内进行，在边界上设置一道障碍，当迭代点靠近D的边上时，惩罚函数的函数值突然增加很快。内点法是求解不等式约束最优化问题的一种十分有效的方法，但不能处理等式约束。

对于目标函数f（X）受约束于g_u（X）≤0（u=1，2，…m）的最优化问题，利用内点法求解时，惩罚函数的一般表达式为

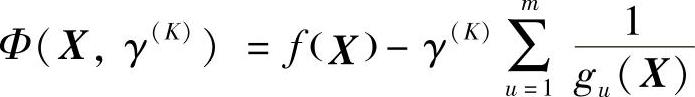
或

对于目标函数F（X）受约束于g_u（X）≥0（u=1，2，…，m）的最优化问题，

即：当K→∞时，γ^（K）→0。

当X为D的内点，且由D的内部靠近D的边界时，总是惩罚项趋于无穷大，这就保证了迭代过程总是在可行域内进行，所以得到的近似最优解总是位于D的内部。

当任何一个约束函数值趋于零时，即意味着迭代点有可行域趋于某边界时，惩罚项的值便将增值无穷大。这个在函数图形上看来，犹如在可行域边界上铸就一道障碍，使迭代点自动保持在可行域内，因而也称为“障碍函数法”。

1）内点法迭代步骤

①在可行域选初始点X^（0）。

②取适当大的初始惩罚因子γ^（0），由无约束最优化方法寻求惩罚函数Φ（X，γ^（0））的最优点X₀^*。

③以所得的X₀^*为下一迭代的新起点，并取一个降低的惩罚因子γ^（1）=Cγ^（0）（0＜C＜1），并用无约束优化方法寻求Φ（X，γ^（1））的最优点X₁^*。

④用上一次无约束最优点作为下一次无约束求优的起点，逐步降低惩罚因子，重复步骤③，不断对惩罚函数Φ进行无约束求优，直到最后满足收敛条件即可终止迭代，并将最终结果作为近似最优解。

上述点列{X₀^*，X₁^*，…，X_K^*}虽然都并非为原目标函数的最优解，但它们却是逐次逼近原函数约束最优点的有序点列。每降低一次惩罚因子，都是对最优解的一次校正，当γ^（K）趋于零时，点X_K^*即收敛于原函数约束最优点X^*。

例11-4 用内点法求目标函数f（X）=ax受约束于g（X）=b-x≤0时的最优解。

解：用内点法求目标函数minf（X）=ax受约束于g（X）=b-x≤0，惩罚函数可写成：

其极值点表达式为

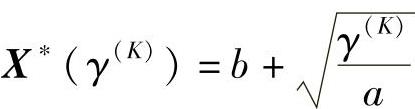
惩罚函数为

从上式可以看出，最优点X^*与最优值Φ（X^*，γ^（K））均为惩罚参数γ^（K）的函数，如图11-7所示。(www.xing528.com)

图11-7 例11-4题图

惩罚函数的极值点不断地沿着一条直线轨迹：

Φ（X^*，γ^（K））=2ax^*-ab所谓直线轨迹，就是图11-7中所标的虚线，该虚线必过两点。一个是最优点（b，ab），另一个是（X^*，Φ（X^*，γ^（K）））（K=1，2，…，m）。

设直线方程为

Y=KX+B

有方程组

由式（1）、式（2）得

由此可得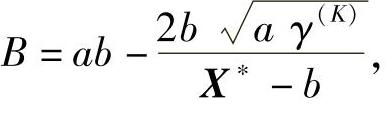故所求直线方程为

Φ（X^*，γ^（K））=2ax^*-ab

2）从约束区内不断地向f（X）的约束最优点X^*接近。当γ^（K）→0时，X^*（γ^（K））→X^*=b，即最后收敛于最优点X^*。

此例说明，惩罚函数法就是以惩罚因子来构造新的目标函数，然后用无约束优化方法求该函数的最优点，而内点法就是将惩罚函数定义在可行域内。

3）几点说明

①初始点X^（0）的选择，内点法要求初始点必须在可行域内。

②初始惩罚参数γ^（0）的选择：γ^（0）选择是否恰当，将显著影响到收敛速度。若γ^（0）过小，即使采用最稳定的无约束优化方法，也存在爬出可行域的危险，使优化步入歧途。若γ^（0）过大，则初次构造的惩罚函数的无约束最优点就离边界约束很远，因而也就离约束最优点X*很远，这将降低计算效率。

③迭代终止准则：

a.前后两次最优值相对插值不超过允许值：

b.前后两次最优点点距不超过允许值：

‖X_K^*-X_K-1^*‖≤δ