如何优化复合形的迭代过程？

在n维设计空间的可行域内，对复合形各个顶点的函数值进行比较，不断去除最坏点，代以既使函数值下降又能满足所有设计约束的新点构成新的复合形，如此反复，使复合形不断减小，并逼近最优点，达到规定精度时则取最后一个复合形的最好的点为最优点。

复合形法的大致过程为：在可行域内选取k个设计点作为初始复合形，这k个设计点作为初始复合形的顶点（n+1≤k≤2n），比较这些顶点的目标函数值，其中最大的点为坏点，以坏点以外其余各点的中心为映射中心寻找坏点的反射点（通常反射点优于坏点）。然后以反射点代替最坏点，形成新的复合形，以此步骤重复多次，使复合形接近最优点。复合形中最小的点作为近似最优点。

下面以二维迭代问题为例：

1）在可行域内取顶点k=4构成初始复合形示意图（见图11-5）：

f（X^（1））＞f（X^（2））＞f（X^（3））＞f（X^（4））

X^（1）→最坏点→X^（H）

X^（2）→次坏点→X^（G）

X^（4）→最好点→X^（L）

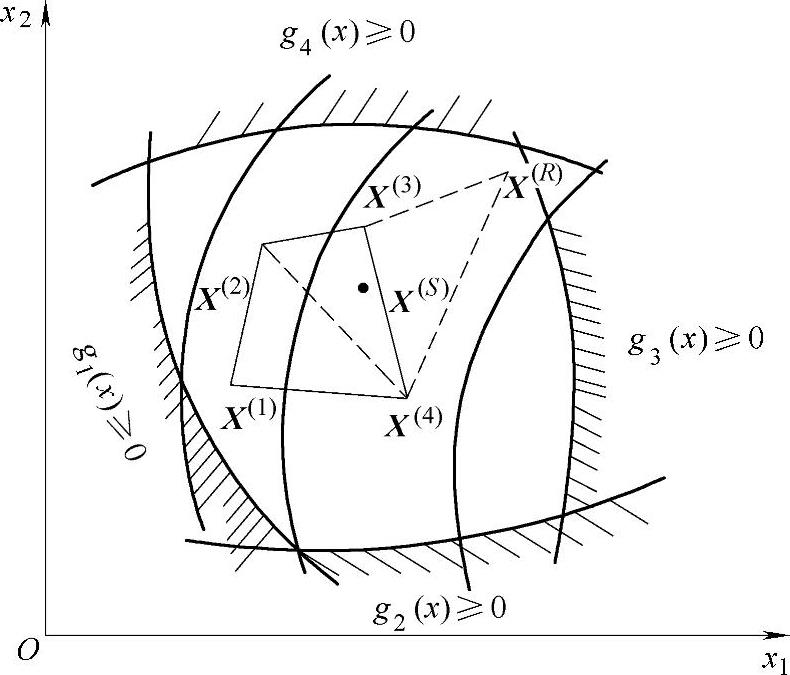
图11-5 复合形法迭代原理

2）求出X^（S）作为映射中心。

X^（S）为去除X^（H）以外其余各点的点集中心（几何中心）。

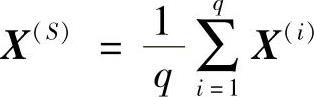
式中 q——顶点个数。

3）找到最坏点X^（H）的映射点X^（R）。X^（H）的映射点X^（R）的迭代公式为(www.xing528.com)

X^（R）=X^（S）+α（X^（S）-X^（H））

式中 α——映射系数（映射方向的步长），α=1.3。

4）若X^（R）满足可行性和适用性要求，则以X^（R）代替X^（H）组成新的复合形，这就完成了“一轮”迭代。

5）若X^（R）不满足可行性和适用性要求之一，则缩减映射系数；，直到α减到很小的规定值而X^（R）仍不能满足要求时，则改用X^（G）的映射方向继续寻找X^（R），找到合适的X^（R）后，则以X^（R）代替X^（H）组成新的复合形，到此完成一轮迭代。图11-5为复合形法迭代原理。

6）通过反复迭代，复合形不断变形并缩小，每当一个新复合形构成之时就用终止迭代条件：

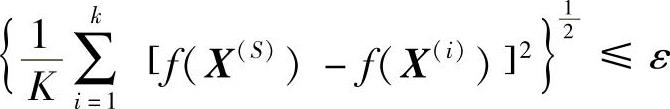
来进行判别。当小于预定精度时，则将复合形中的最好点输出。

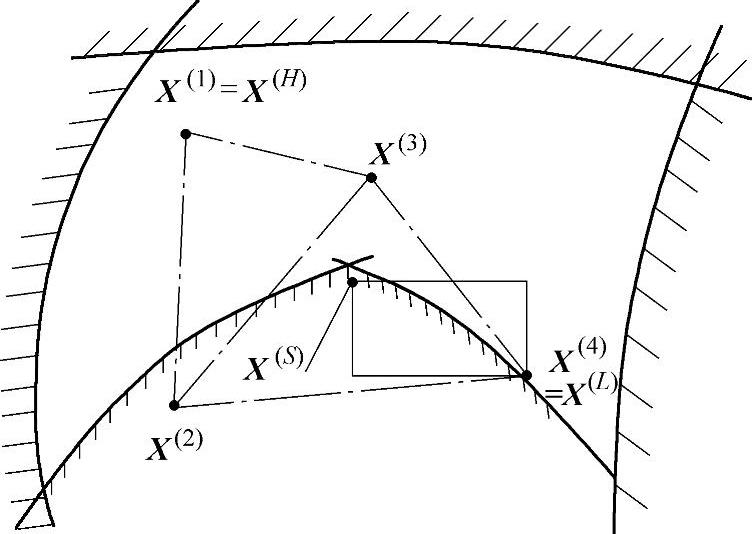
图11-6 复合形法的特殊情况

有一种特殊情况还要考虑，即映射中心X^（S）不在可行域内，则可行域可能是一个非凸集，如图11-6所示。这时为了将X^（S）点移进可行域内，可在以X^（L）点和X^（S）点为界的超立方体中（二维则为长方形），重新利用伪随机数产生K个新的顶点，构成新的复合形。此时变量的上下限改为：

若x_i^（L）＜x^（S） （i=1，2，…，n），则取

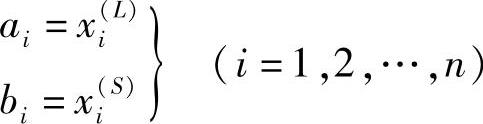
否则相反。随后将各域外的随机顶点调入域内。