DFP法迭代步骤优化

DFP法迭代步骤为：

1）给定初始点X⁰∈Rⁿ，迭代精度ε，维数n。

2）置0⇒k，单位矩阵I⇒A⁰，计算▽f（X^k）⇒g⁰。

3）计算搜索方向-A^kg^k⇒S^k。

4）进行一维搜索求α^k，得迭代新点

X^k+α^kS^k⇒X^k+1

5）检验是否满足迭代条件

‖▽f（X^k+1）‖≤ε？

若满足，则停止迭代，输出最优解X^k+1⇒X^*，f（X^k+1）⇒f（X^*）；否则进行下一步。

6）检查迭代次数，若k=n，则置X^k+1⇒X⁰，转2）步；若k＜n，则转7）步。

7）计算：X^k+1-X^k⇒ΔX^k，▽f（X^k+1）⇒g^k+1，g^k+1-g^k⇒Δg^k，按式计算ΔA^k，A^k+ΔA^k⇒A^k+1。然后，置k+1⇒k，转3）步。

例10-4 用DFP法解决下列无约束优化问题

f（X）=4（x₁-5）²+（x₂-6）²的极小点和极小值，取初始点X⁰=[8 9]^T，梯度精度ε=0.01。

解：取初始点X⁰=[8 9]^T，这时有f（X⁰）=45

目标函数的梯度函数为

第一次迭代

第一次迭代

计算X⁰点的导数值：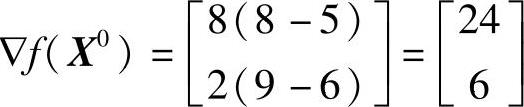

求搜索方向S⁰及新的迭代点X¹：

计算X⁰点的导数值：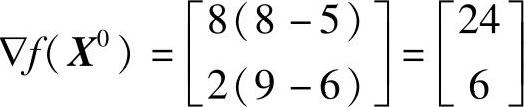

求搜索方向S⁰及新的迭代点X¹：

用一维优化方法来求解最优步长α⁰，但因本题的目标函数简单，可用解析法求α⁰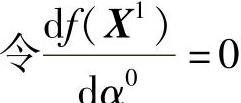：，得(www.xing528.com)

4680α⁰-612=0⇒α⁰=0.130769

于是得

用一维优化方法来求解最优步长α⁰，但因本题的目标函数简单，可用解析法求α⁰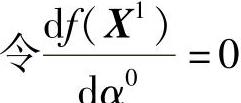：，得

4680α⁰-612=0⇒α⁰=0.130769

于是得

计算X¹点的函数梯度，检验迭代终止条件：

计算X¹点的函数梯度，检验迭代终止条件：

因此，X¹不是极小点，须继续迭代。

第二次迭代：

因此，X¹不是极小点，须继续迭代。

第二次迭代：

按DFP公式计算变尺度矩阵A¹

按DFP公式计算变尺度矩阵A¹

求搜索方向S¹及新的迭代点X²

求搜索方向S¹及新的迭代点X²

沿S¹方向进行一维搜索，得

沿S¹方向进行一维搜索，得

检验迭代终止条件：

检验迭代终止条件：

满足精度要求，迭代结束，输出最优解：

满足精度要求，迭代结束，输出最优解：