阻尼牛顿法详解

从牛顿法迭代公式的推演中可以看到，迭代点的位置是按照极值条件确定的，其中并未包含有沿下降方向搜索的概念。因此对于非二次函数，如果采用上述牛顿迭代公式，有时会使函数值上升，从而出现f（X^k+1）＞f（X^k）的现象。为此，需对上述牛顿法进行改进，引入数学规划法的搜寻概念，提出所谓“阻尼牛顿法”。

如果我们把d^k=-[▽²f（X^k）]^-1▽f（X^k）看作是一个搜索方向，称其为牛顿方向，则阻尼牛顿法采用如下的迭代公式：

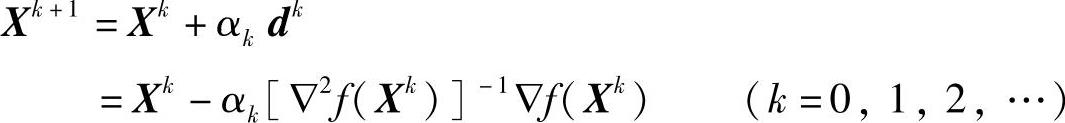
式中 α_k——沿牛顿方向进行一维搜索的最佳步长，可称为阻尼因子。

α_k可通过如下极小化过程求得：

f（X^k+1）=f（X^k+α^kd^k）=minf（X^k+αd^k）

这样，原来的牛顿法就相当于阻尼牛顿法的步长因子α_k取成固定值1的情况。由于阻尼牛顿法每次迭代都是在牛顿方向上进行一维搜索，这就避免了迭代后函数值上升的现象，从而保持了牛顿法二次收敛的特性，面对初始点的选取并没有苛刻的要求。

阻尼牛顿法的计算步骤如下：(www.xing528.com)

1）给定初始点X⁰，收敛精度ε，置k←0。

2）计算▽f（X^k）、▽²f（X^k）、[▽²f（X^k）]^-1和d=-[▽²f（X^k）]^-1▽f（X^k）。

3）求X^k+1=X^k+α_kd^k，其中α_k为沿d^k进行一维搜索的最佳步长。

4）检查收敛精度。若‖X^k+1-X^k‖＜ε，则X^*=X^k+1，停止计算；否则，置k←k+1，返回到第2）步继续进行搜索。

阻尼牛顿法的程序框图如图10-9所示。

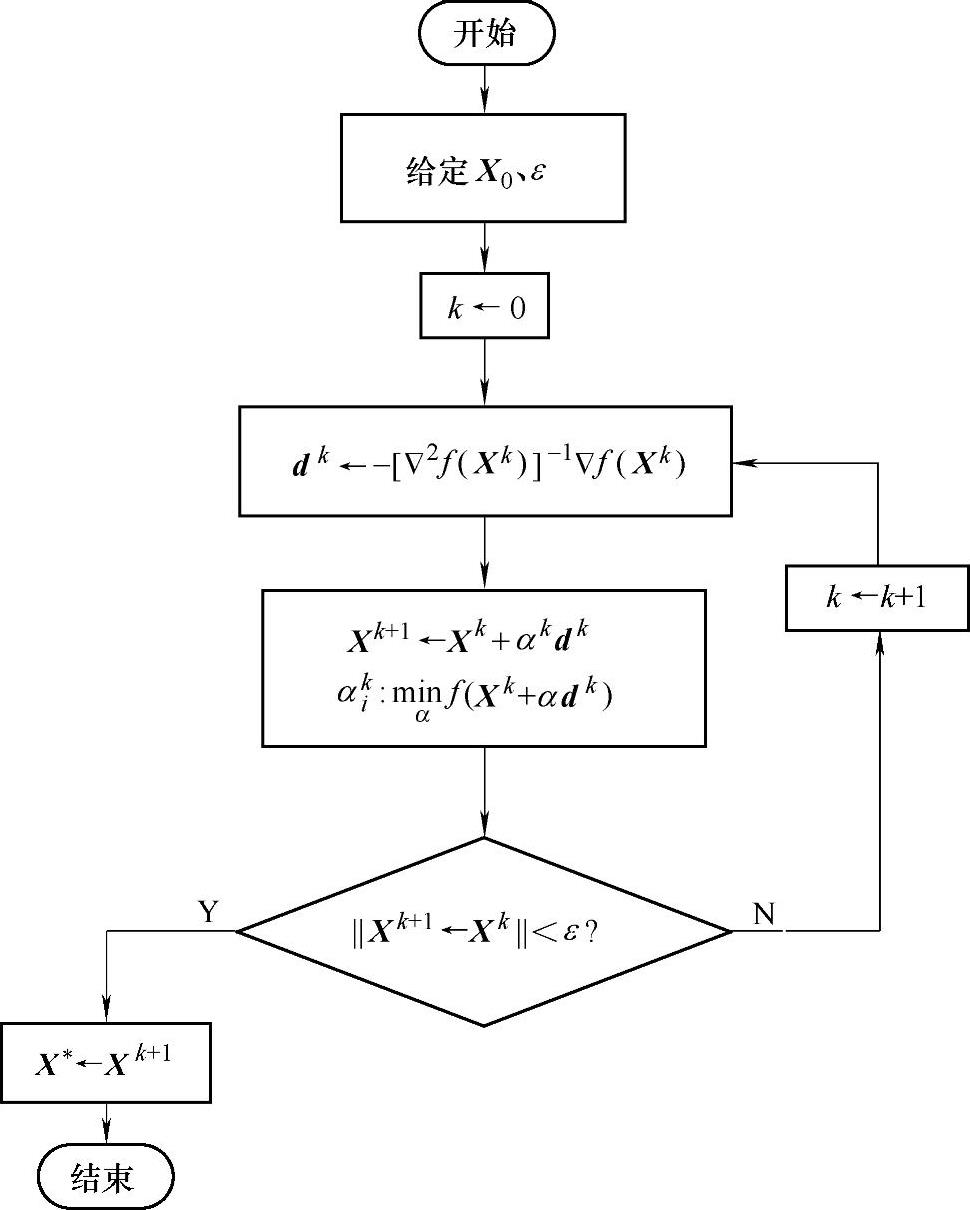
图10-9 阻尼牛顿法的程序框图