鲍威尔算法优化措施

在鲍威尔基本算法中，每一轮迭代都用连接始点和终点所产生的搜索方向去替换原向量组中的第一个向量，而不管它的“好坏”，这是产生向量组线性相关的原因所在。因此在改进的算法中首先判断原向量组是否需要替换。如果需要替换，还要进一步判断原向量组中哪个向量最坏，然后再用新生成的向量替换这个最坏的向量，以保证逐次生成共轭方向。

改进算法的具体步骤如下：

1）任选初始点X⁰（记为X⁰₀），任选初始方向组，它由n个线性无关的向量（如n个坐标轴单位向量e₁，e₂，…，e_n）组成，置k←0。

2）从X₀^k出发，顺次沿这n个线性无关的向量作一维搜索得到点X^k₁，X^k₁，X₂^k，…，X^k_n。接着以X^k_n为起点，沿方向S^k_n+1=X^k_n-X₀^k移动一个X^k_n-X₀^k的距离，得

X^k_n+1=2X^k_n-X₀^k

X₀^k、X^k_n、X^k_n+1，分别称为一轮迭代点的始点、终点和反射点。始点、终点和反射点所对应的函数值分别表示为

F=f（X^k₀）

F=f（X^k_n）

F=f（X^k_n+1）

同时，计算各中间点的函数值，并记为

f_i=f（X^k_i） （i=0，1，2，…，n）

因此，有F₀=f₀，F₂=f_n。

计算n个函数值之差f₀-f₁，f₁-f₂，…，f_n-1-f_n。记作

Δ_i=f_i-1-fi （i=0，1，2，…n）

其中最大值记作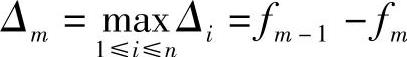（i=0，1，2，…，n）。

3）根据是否满足判别条件

F₃＜F₀

和

（F₀-2F₂+F₃）（F₀-F₂-F_m）²＜0.5Δ_m（F₀-F₃）²

来确定是否要对原方向组进行替换。

若不满足条件判断，则下轮迭代仍用原方向组，并以X^k_n、X^k_n+1中函数值小者作为下轮迭代点。

若满足上述判别条件，则下轮迭代应对原方向组进行替换，将S^k_n+1、S^k补充到原方向组的最后位置，而除掉S^k_m。即新方向组为S^k₁，S₂^k，…，S^k_m-1，S^k_m+1，S^k_n，S^k_n+1作为下轮迭代的搜索方向。下轮迭代的始点取为沿S^k_n+1方向进行一维搜索极小点X₀^k+1。

4）判断是否满足收敛准则。若满足取X₀^k+1为极小点，否则应置k←k+1，返回步骤2），继续进行下一轮迭代。

这样重复迭代的结果，后面加进去的向量都彼此对H共轭，经n轮迭代即可得到一个由n个共轭方向所组成的方向组。对于二次函数，最多不超过n次就可找到极小点，而对一般函数，往往要超过n次才能找到极小点（这里的“n”表示设计空间的维数）。如果在n轮迭代后还未收敛，一般应该重新选择单位向量为迭代的初始方向进行迭代。

例10-2 用鲍威尔法求函数

f（x₁，x₂）=10（x₁+x₂-5）²+（x₁-x₂）²的极小值。

解：选初始点X⁰₀=[0 0]^T，初始搜索方向S⁰₁=e₁=[1 0]^T，S⁰₂=e₂=[0 1]^T。初始点处函数值F₀=f₀=f（X⁰₀）=25。

第一轮迭代：

1）沿S⁰₁方向进行一维搜索得

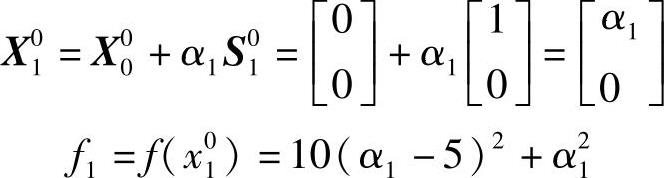
最佳步长α₁可通过下式获得

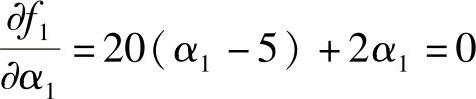
即

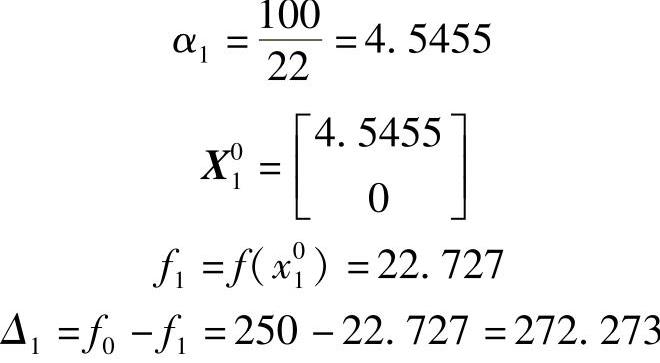
2）再沿S⁰₂方向进行一维搜索得

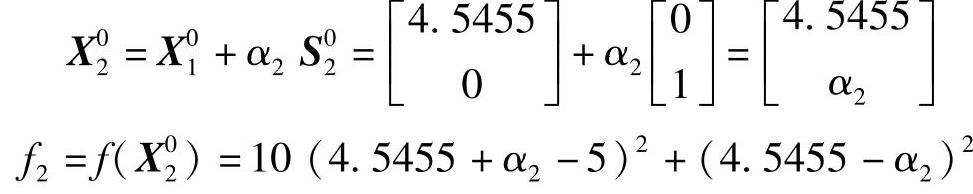
最佳步长α₂的计算可根据：

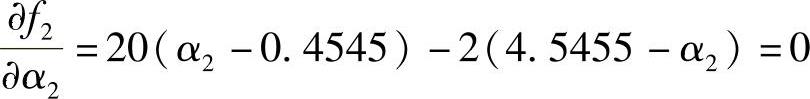
进行，得

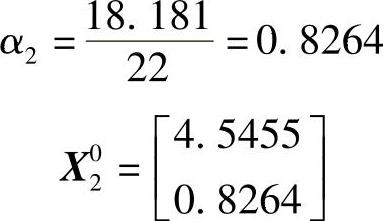
从第一轮终点X⁰₂处出发，沿S⁰₂走一步后的函数值增量为

F₂=f₂=F（X⁰₂）=15.214

Δ₂=f₁-f₂=22.727-15.214=7.513(www.xing528.com)

沿S⁰₁、S⁰₂寻优后函数值增量中的最大者为

Δ_m=Δ₁=227.273

终点X⁰₂的反射点及其函数值为

F₃=f（X⁰₃）=385.24

3）为确定下一轮迭代的搜索方向和起始点，需检查判别条件F₃＜F₀和（F₀-2F₂+F₃）（F₀-F₂-Δ_m）²＜0.5Δ_m（F₀-F₃）²是否满足。

因为F₃＞F₀，所以不满足判别条件，因而下轮迭代中应该继续使用原来的搜索方向e₁、e₂。

因为F₂＜F₃，所以取X⁰₂作为下轮迭代的起始点。

第二轮迭代：

第二轮初始点及其函数值：

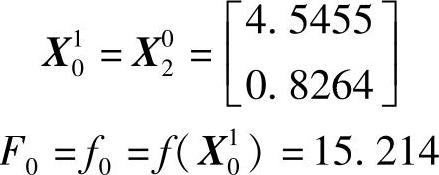
1）沿e₁方向（即x₁轴方向）进行一维搜索，相当于固定x₂=0.826，改变x₁使函数F（x₁，x₂）的值极小。设计点X¹₁位置可通过函数对x₁的偏导数等于零求得，即

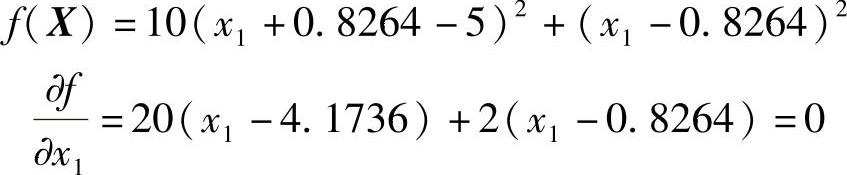
得

X¹₁点处的函数值及函数值增量分别为

f₁=f（X¹₁）=10.185

Δ₁=f₀-f₁=15.214-10.185=5.029

2）再沿方向e₂（即x₂轴方向）进行一维搜索，相当于固定x₁=3.869，改变x₂使函数f（x₁，x₂）的值极小。设计点X₂¹位置可通过函数对x₂的偏导数等于零求得，即

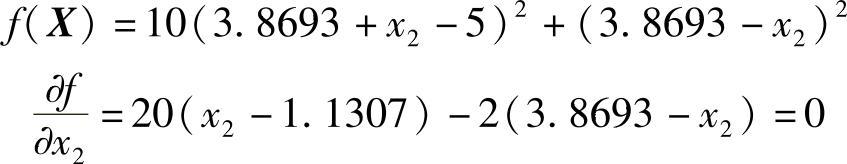
得

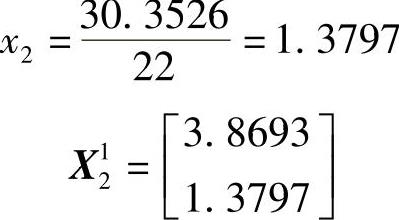
第二轮终点X₂¹处的函数值及沿x₂方向函数值增量分别为

F₂=f₂=f（X₂¹）=6.818

Δ₂=f₁-f₂=10.185-6.818=3.367

取Δ₁、Δ₂函数值增量中的最大者：

Δ_m=Δ₁=5.029

终点X₂¹的反射点及其函数值为

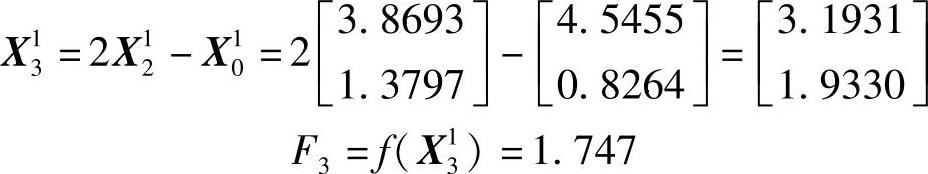
3）为确定下一轮迭代的搜索方向和起始点，需检查判别条件F₃＜F₀和（F₀-2F₂+F₃）（F₀-F₂-F_m）²＜0.5Δ_m（F₀-F₃）²，经代入运算知该判别条件满足，应进行方向替换。用新方向S₃¹替换e₁，下轮迭代搜索方向为e₂、S₃¹，且

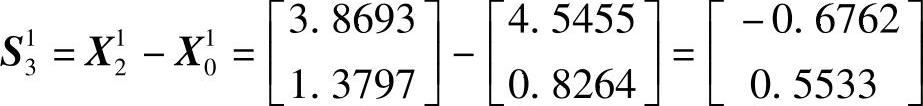
下轮迭代起始点X²₀为从X₂¹出发，沿S₃¹方向进行一维搜索的极小点，可通过下面计算求得：

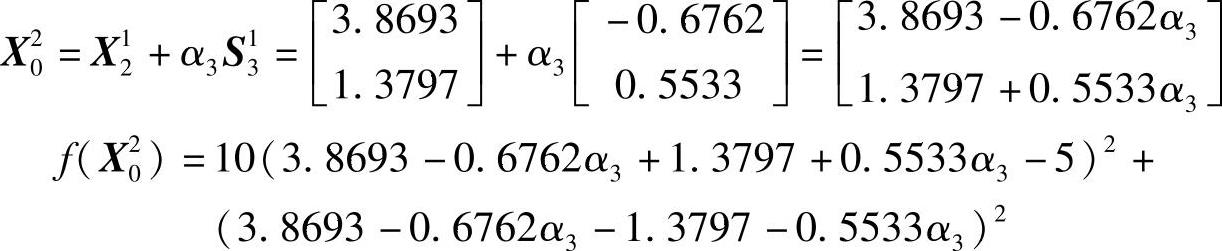
通过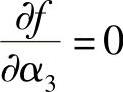

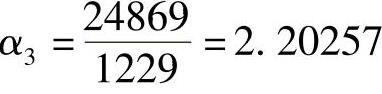
得下轮迭代初始点及其函数值为

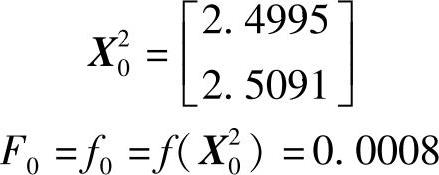
可见已足够接近极值点X^*=[2.5 2.5]^T及极小值f（X^*）=0。

该方法是一种非常有效的共轭方法，它可以在有限步内找到二次函数的极小值。对于非二次函数只要具有连续二阶导数，用这种方法也是有效的。

鲍威尔改进算法的程序框图如图10-6所示。

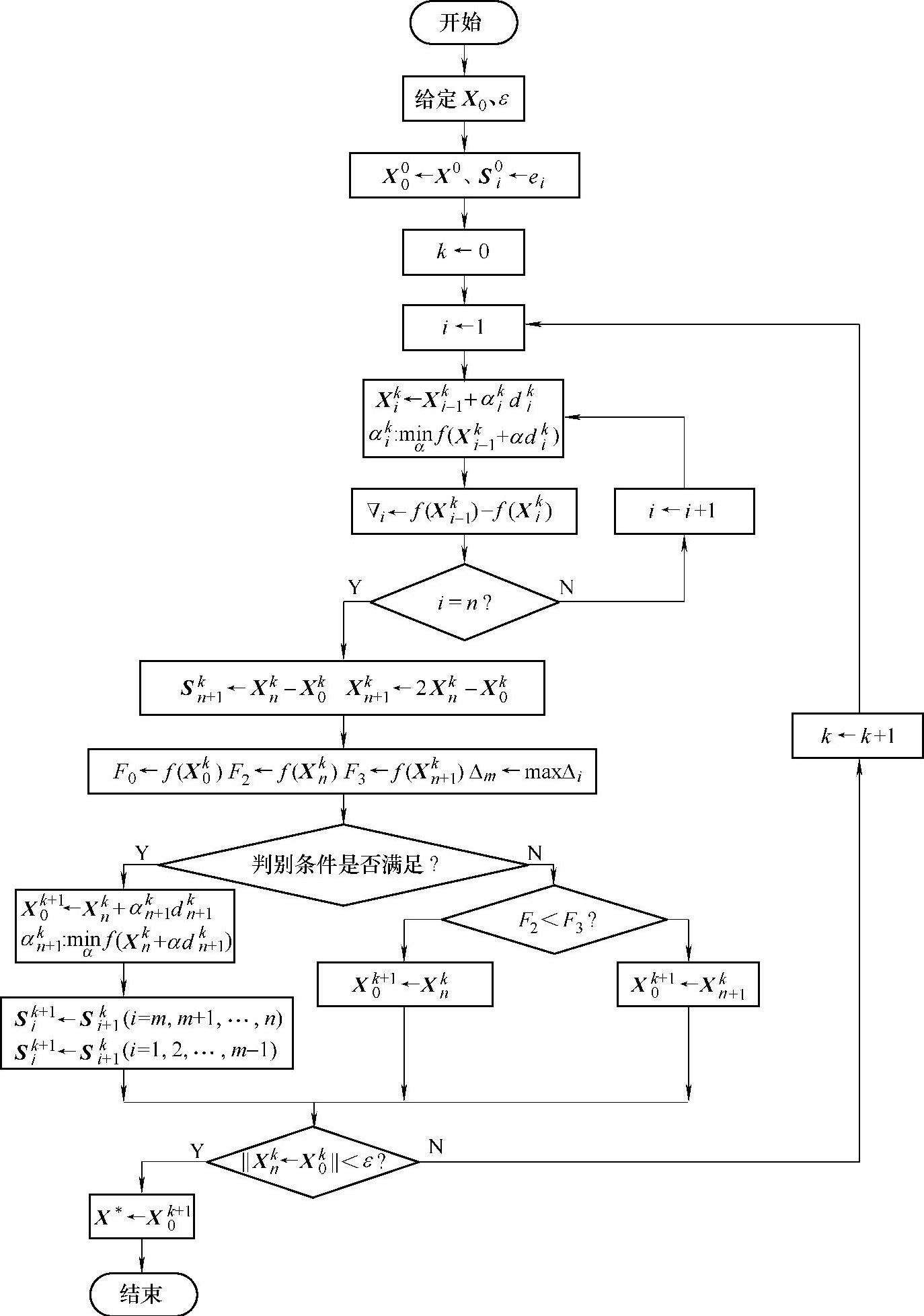
图10-6 鲍威尔改进算法程序框图