黄金分割法-一维优化搜索

黄金分割法也称0.618法。本法也是应用序列消去法原理的直接探索法。其做法是通过对分割点函数值进行比较来逐次缩短区间。

对于目标函数f（x），给定初始搜索区间[a，b]，收敛精度为ε。

首先，在初始搜索区间内部取两个点x₁与x₂（见图9-4），x₁＜x₂且在区间内处对称位置，两点的对应值为

y₁=f（x₁），y₂=f（x₂）

比较y₁和y₂的大小，有下面两种情况：

1）若有y₁＜y₂，如图9-4a所示，极小点必在区间[a，x₂]内，此时令b←x₂，新的区间为[a，x₂]。

2）若有y₁≥y₂，如图9-4b所示，极小点必在区间[x₁，b]内，此时令a←x₁，缩短后的新区间为[x₁，b]。

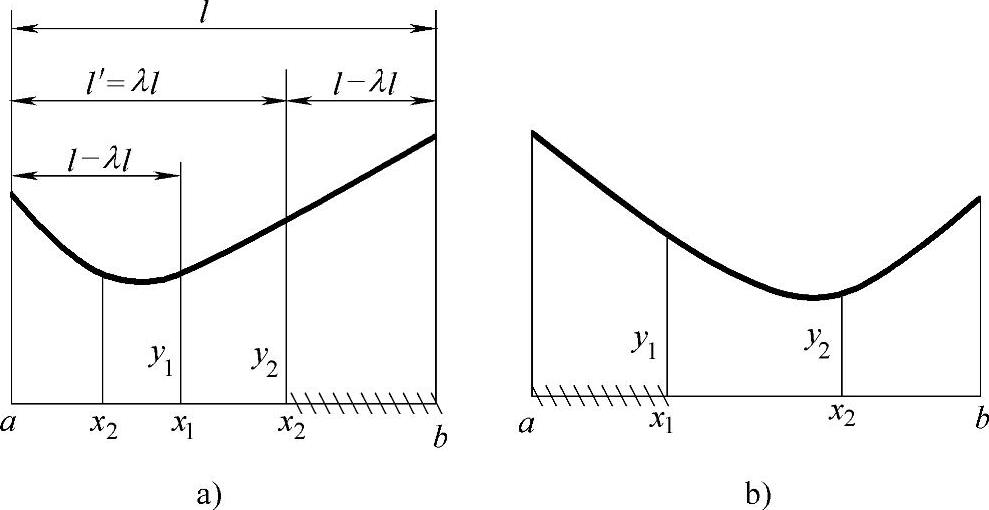
图9-4 黄金分割法缩短区间

经过对两内点函数值的比较，区间缩短一次。缩短后的新区间是原区间的一部分，即舍去阴影线部分，留下其左面或者右面部分，其间保留着原来两内点x₁与x₂当中的一个，则新的区间中只有一个内点。

为了进行下一次的缩短区间，则在新区间中再以对称原则增补一个内点，重复上述函数值的比较，如此反复分割，使区间依次地加以缩短。

黄金分割法内分点选取的原则之一是要对称的，并采取每次区间缩短率都是相等的，按以上原则，其区间缩短率应是λ≡0.618。简单推证如下（参见图9-4a）：

设初始区间长度为l，第一次区间缩短率为λ₁，则第一次新区间长度l₁=λ₁l，新区间为[a，x₂]。进行第二次缩短时，要在区间[a，x₂]中增补一个内点x₃，计算y₁=f（x₃），经比较有y₁＞y₃，于是第二次的新区间为[a，x₁]。l由第一次区间内点x₁与x₂的对称性可知，区间[a，x₁]之长度l₂=（1-λ₁）l。本次区间缩短率为λ₂，则

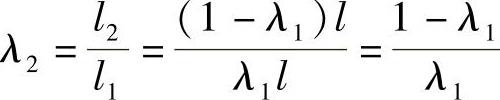
要求两次缩短率相等，即λ₂=λ₁=λ，得方程

λ²+λ-1=0

方程的合理根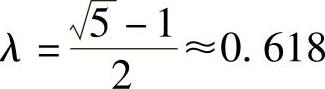

由于黄金分割法取两个内点x₁与x₂为对称，且区间缩短率λ≡0.618。则内分点的取点规则为

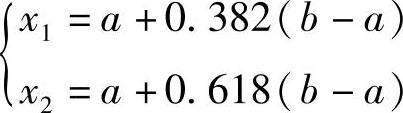
由于黄金分割法是按等区间缩短率，且λ≡0.618，当取初始搜索区间为[a，b]，收敛精度为ε。要求搜索到最终区间长度满足收敛精度ε，则缩短区间的次数k应满足

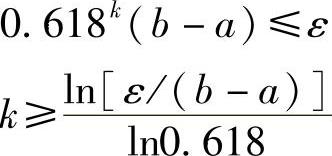
上面两式是黄金分割法的终止准则。

用黄金分割法进行一维优化搜索，当满足终止准则后，即停止计算。取最终收缩区间的中点为近似最优点，最优解为

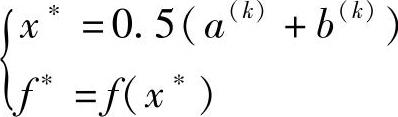(www.xing528.com)

黄金分割法的流程图如图9-5所示。

例9-1 试用黄金分割法求目标函数f（x）=x²-6x+9的最优解。给定初始区间[1，7]，收敛精度ε=0.4。

解：首先计算第一次区间缩短。

计算两内点及对应函数值：

x₁=a+0.382（b-a）=3.292，y₁=f（x₁）=0.085264

x₂=a+0.618（b-a）=4.708，y₂=f（x₂）=2.917264

作函数值比较，可见y₁＜y₂，再作置换：

a^（1）←a=1，b^（1）←x₂=4.708

用终止准则判断：

b^（1）-a^（1）=4.708-1=3.708＞ε

为第二次区间缩短做准备，作置换：

x₂←x₁=3.292，y₂←y₁=0085264

x₁=a^（1）+0.382（b^（1）-a^（1））=2.416456，y₁=f（x₁）=0.340524

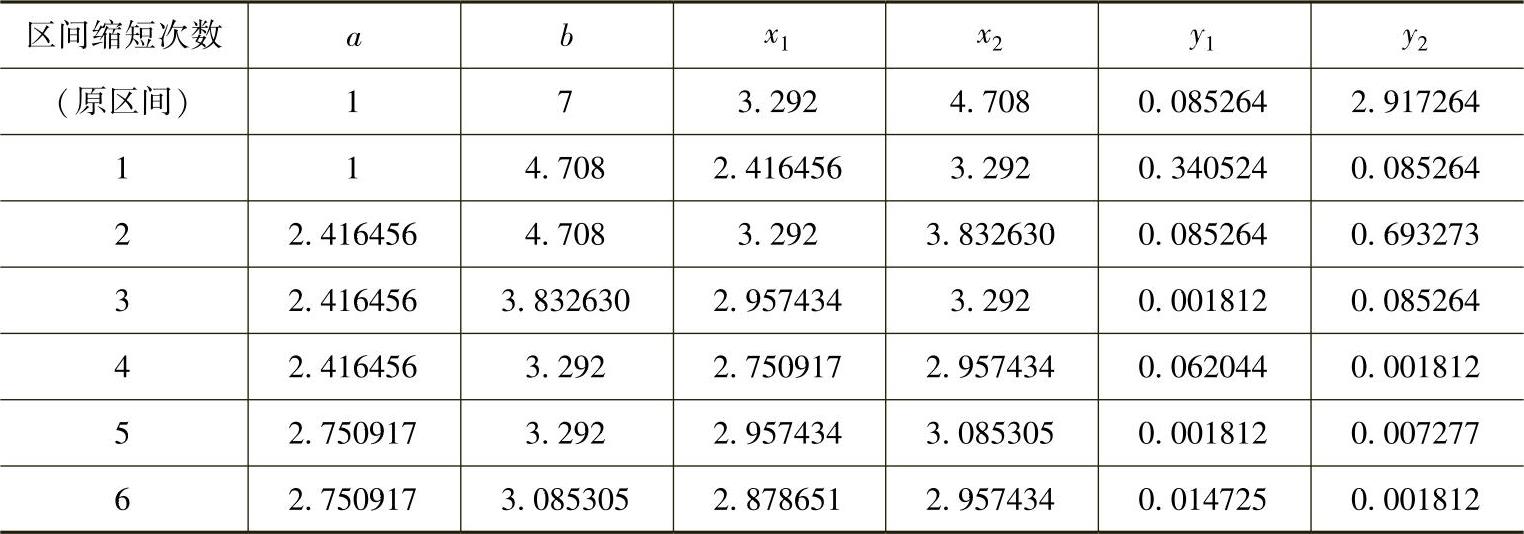
各次缩短区间的计算数据见表9-1。

第六次区间缩短的端点

a^（6）=2.750917，b^（6）=3.085305，b^（6）-a^（6）=0.334388＜ε

满足精度要求，终止计算。取最优解为

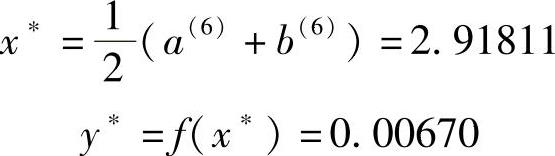
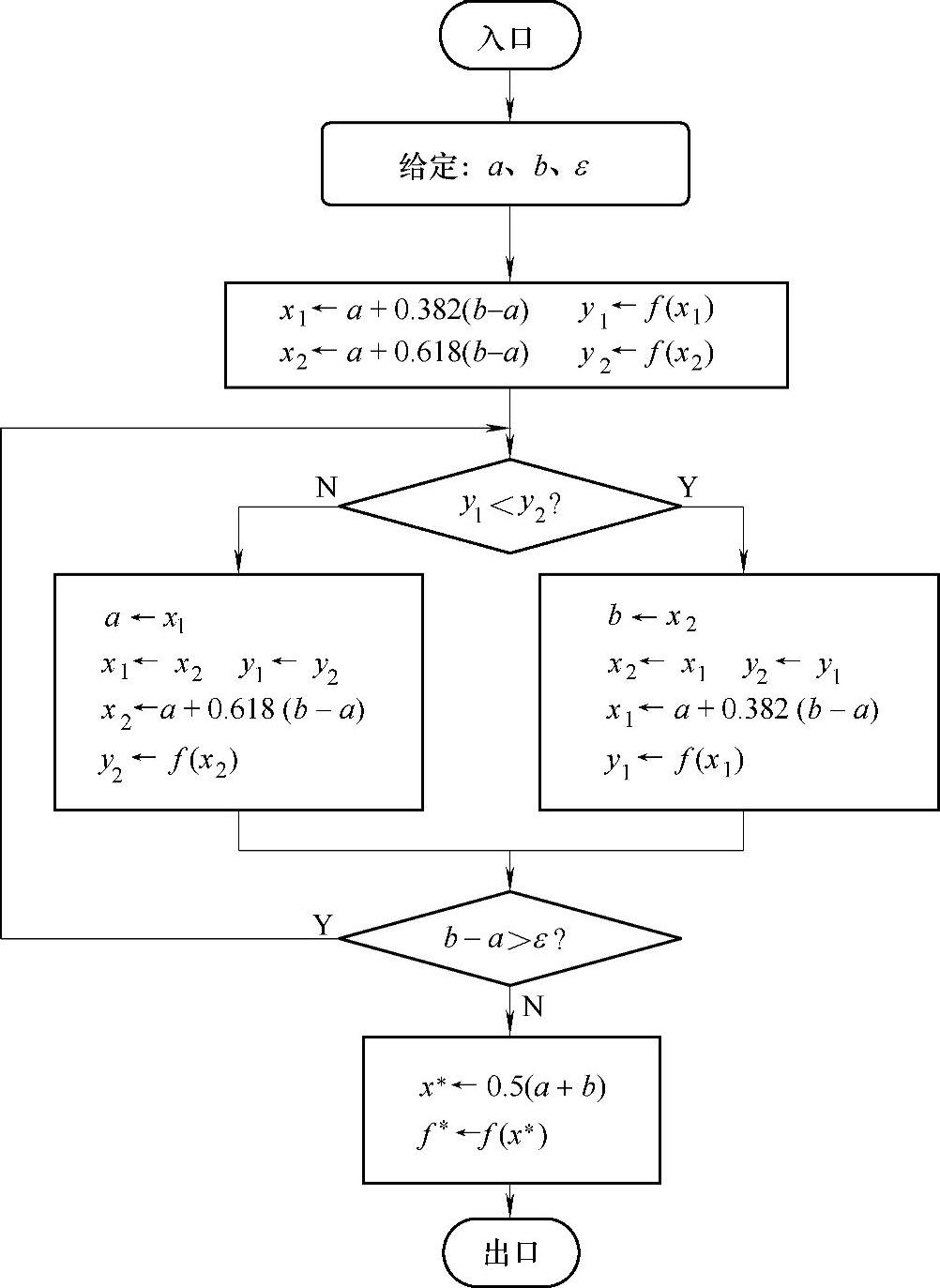
图9-5 黄金分割法的流程图

表9-1 黄金分割法例题计算数据