二元函数的梯度计算方法详解

设有二元函数f（X）=f（x₁，x₂），它在x₀点处的方向导数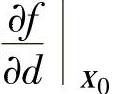的表达式可以写成下面的形式：

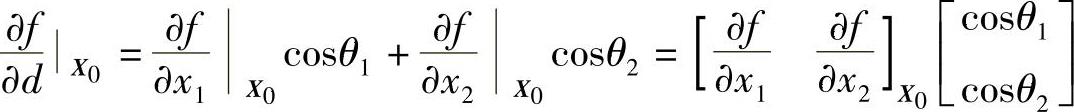
令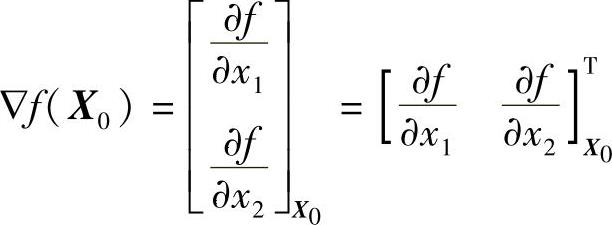

上式即被称为函数f（x₁，x₂）在X₀点处的梯度。

设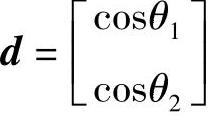

则有

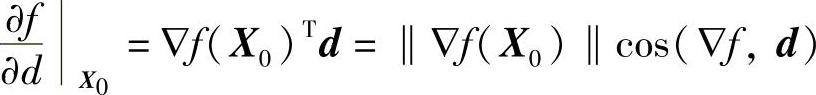
其中▽f（X₀）代表梯度向量的模，cos（▽f，d）表示梯度向量与d方向夹角的余弦。

这一关系式表明了函数在某点的梯度和函数在这点的方向导数之间的关系，在X₀点处沿各方向的方向导数是不同的，是随cos（▽f，d）变化的。当cos（▽f，d）=1时，也就是当梯度方向和d方向重合时方向导数的值最大。可见梯度方向就是函数值变化最快的方向，梯度的模就是函数变化率的最大值。

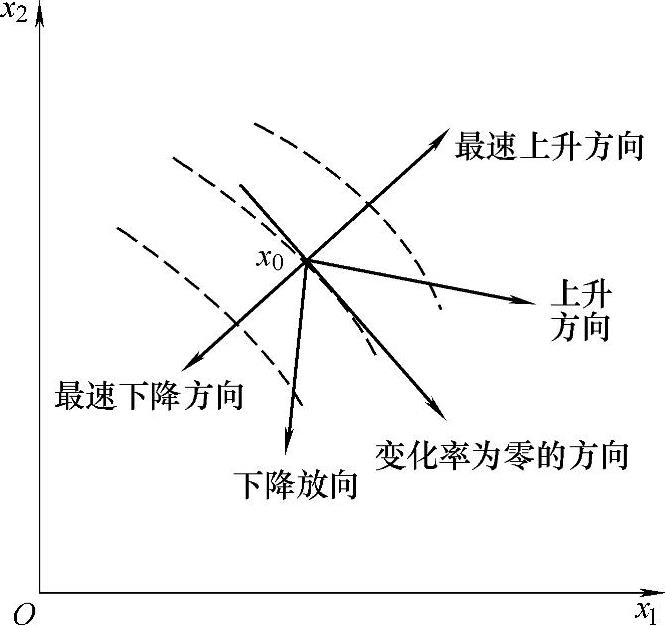
图8-5 函数值变化方向

在x₁-x₂平面内f（x₁，x₂）的等值线f（x₁，x₂）=c，如图8-5所示，在x₀处的等值线的切线方向d是函数变化率为零的方向，即(https://www.xing528.com)

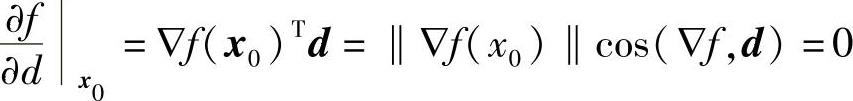
也即 cos（▽f，d）=0

可知梯度▽f（X₀）和切线方向d垂直，从而可以看出，梯度的方向是等值面的方向。梯度▽f（X₀）的方向是函数变化率最大的方向，也就是最速上升方向。负梯度-▽f（X₀）的方向为函数变化率取最小值的方向，即最速下降方向。与梯度成锐角的方向为函数上升方向，与负梯度成锐角的方向为函数下降方向。

上述二元函数的梯度概念可以推广到二元以上的多元函数中去，函数f（x₁，x₂，…，x_n）在点X₀（x₁₀，x₂₀，…，x_n0）处的梯度▽f（X₀）定义为

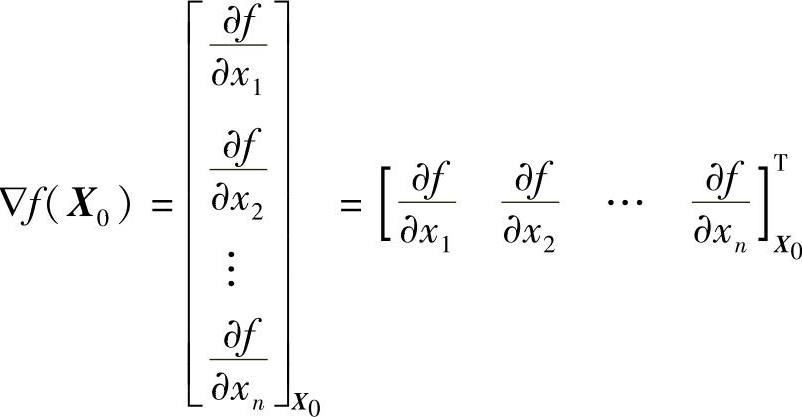
梯度▽f（X₀）的模为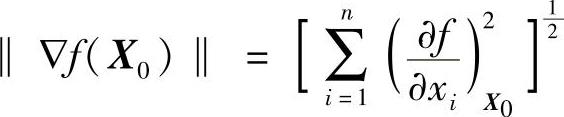

梯度方向的单位向量为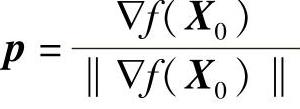

它和函数等值面f（X）=c相垂直，也就是和等值面上过X₀的一切曲面相垂直，如图8-6所示。

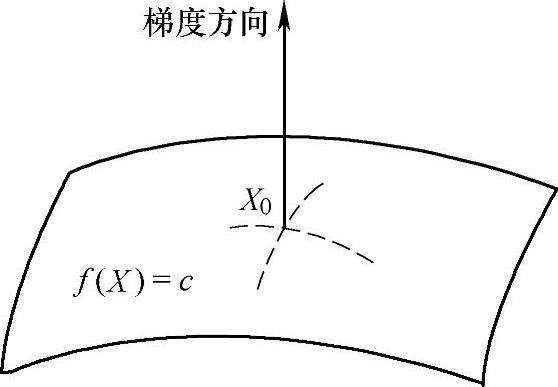
图8-6 梯度方向