正定二元二次型函数的性质

正定函数的一般形式为

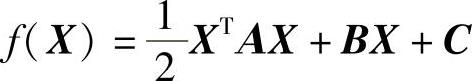
式中 A——n×n正定对称矩阵。

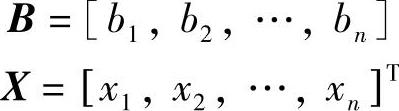
上式这样的函数对优化问题是具有很重要的意义的。上式中，当维数n=2时，该式就代表正定二元二次函数。对于二元二次函数有两个重要的性质：

性质1：正定二元二次型函数的等值线是同心椭圆族，且椭圆的中心就是以该函数为目标函数的极小点。

设：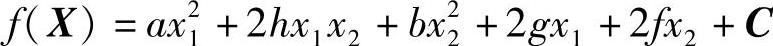

写成矩阵形式为

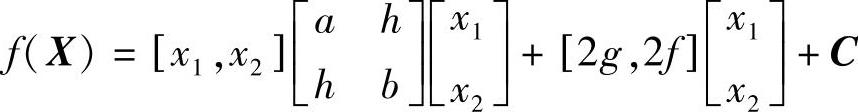
当a＞0，ab-h²＞0时，矩阵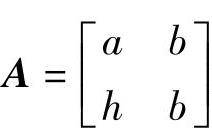为正定。

当ab-h²＞0时，此二次曲线为一椭圆。令：

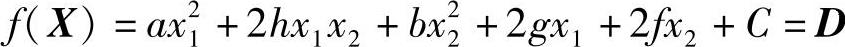
当D的数列为d₁＞d₂＞d₃＞…时，此二次曲线是一族同心椭圆，所以正定二元二次函数的等值线是椭圆族，如图8-1所示。

当上式右端常数D取值越来越小时，所对应的等值线椭圆也越来越小。当D趋于零时，等值线椭圆缩小成椭圆中心的一个点。显然，此时函数f（X）具有极小值，并且椭圆中心的坐标值就是正定二元二次函数的极小点。

正定二元二次型函数的这个概念完全可以推广到n=3及多维设计问题的分析中去，只不过对于三维问题，在设计空间对应的应是目标函数的“等值面”、“同心椭球面族”；椭球面的中心正好是极值（小）点；高于三维的问题（n＞3），在设计空间中将是“超椭球面”（多维正定二次函数的超等值面），无法用三维图形表示，是一个抽象的概念。

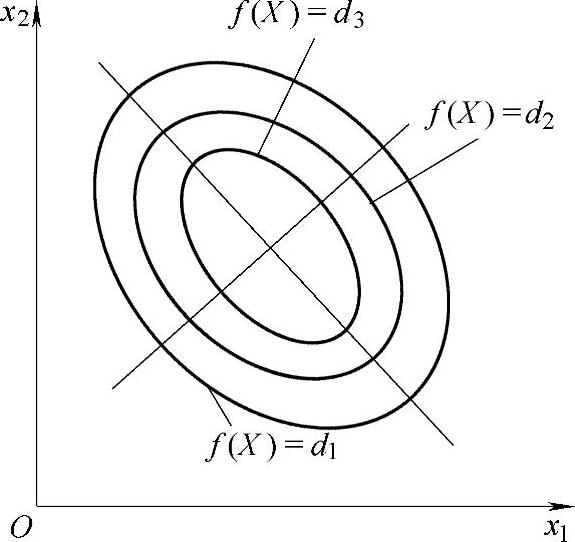
图8-1 正定二元二次函数等值线

性质2：过同心椭圆族中心，作任意直线与椭圆族中任意两椭圆相交，通过交点所作的椭圆的切线必相互平行。(www.xing528.com)

为了简化运算，令原点中心为椭圆中心，则可设f（X）为

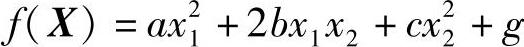
其中a＞0，ac-b²＞0

设直线方程为x₂=kx₁，与椭圆

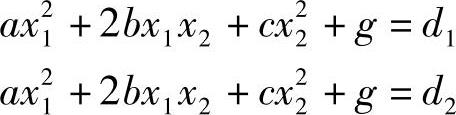
的交点分别为M、N，如图8-2所示。下面求这两点处的斜率。

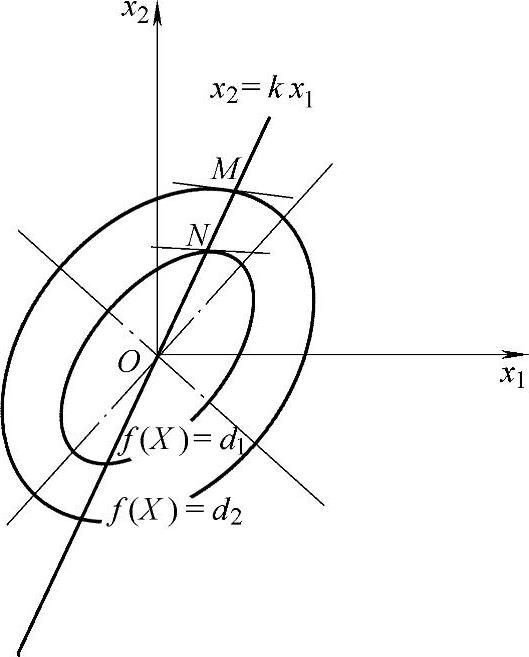
图8-2 同心椭圆族

椭圆方程对x₁求导得：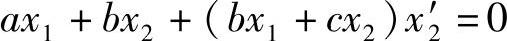

得出在点（x₁，x₂）处的斜率：

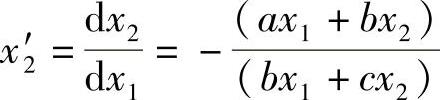
将x₂=kx₁代入，得

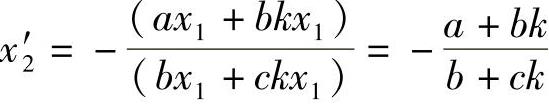
上式说明，过椭圆中心的直线与椭圆族交点处的斜率为常数，故各交点处的切线平行。

根据这一性质，如果沿两条与给定方向平行的直线，求出两直线与椭圆族中某两椭圆的切点M、N，过此两点的直线必通过椭圆族的中心，即函数的极小点。

换句话说：若沿着M、N两点连线方向搜索，就可以找到f（X）的极小点。这一特性在建立了共轭方向的概念之后就知道，它对产生某些优化算法有着重大意义。