优化设计的数值迭代计算法

1.数值计算法的迭代过程

最优化方法是与电子计算机及计算技术的发展紧密相联系的，数值计算法的迭代过程也是依赖于计算机的运算特点而形成的，所以，计算过程完全有别于解析法的求解过程。优化方法的迭代特点是：按照某种人为规定的逻辑结构，以一定的格式进行反复的数值计算，寻求函数值逐次下降的设计点，直到满足规定的精度时终止迭代计算，最后的设计点即为欲求的最优点，所得到的解是满足规定精度的近似解。

总体的做法如图7-8所示，由选定的初始点X^（0）出发，沿某种优化方法所规定的搜寻方向S^（0），以适当的步长α^（0），按迭代格式产生第一个新的设计点X^（1）

X^（1）=X^（0）+α^（0）S^（0）

使满足 f（X^（1））＜f（X^（0））

则X^（1）是优于X^（0）的设计点。再以X^（1）为新的起点，按同上的格式产生第二个设计点X^（2）

X^（2）=X^（1）+α^（1）S^（1）

这样，依次得设计点X^（1）、X^（2）、X^（3）、…X^（k）、X^（k+1）、…，称这样的点为计算中的迭代点，产生迭代点的一般格式为

X^（k+1）=X^（k）+α^（k）S^（k）

上式称为优化设计的基本迭代公式。式中的第k次搜寻方向S^（k）及步长α^（k）是根据X^（k）点的目标函数值和约束函数值等信息确定的，使其f（X^（k+1））＜f（X^（k））。按上述迭代公式反复迭代计算后产生点列X^（1）、X^（2）、X^（3）、…X^（k）、…，各点的函数值依次下降，即f（X^（0））＞f（X^（1））＞f（X^（2））＞…＞f（X^（k））＞…。显见迭代点不断向理论最优点逼近，最后必将到达满足预定精度要求的近似最优点，记作X^*。

图7-8 二维优化问题迭代过程

由迭代算法的基本迭代公式可见，优化方法的主要问题乃是解决迭代方向

S^（k）（k=1，2，…）和迭代步长α^（k）（k=1，2，…）的问题，由于S^（k）与α^（k）的确定方法及特性的不同而构成了不同的优化方法，即最优化方法。已有的各种优化方法尽管在选取方向和步长的原则上各有千秋，但有一点是共同的，就是上述的基本迭代公式，通过电子计算机进行数值计算，且保证目标函数值稳定地下降，最终获得逼近理论最优点的近似解。

2.迭代计算的终止准则

数值计算采用迭代法产生设计点的点列X^（1）、X^（2）、X^（3）、…X^（k）、…。从理论上讲，任何一个迭代算法都能产生无穷点列{X^（k），k=0，1，2，…}，但在解决实际计算过程中总不能无限制地进行下去，那么什么时候截断迭代，这是一个迭代终止准则问题。

优化设计是要求出设计问题的最优解，从理论上，人们当然希望最终迭代点到达理论极小点，或者使最终迭代点与理论极小点之间的距离足够小时即可终止迭代。但这在实际计算中是办不到的，因为对于一个待求的优化问题，其理论极小点在哪里并不知道，所知道的只是通过迭代计算，得到迭代点的序列{X^（k），k=0，1，2，…}。因此，只能通过上述点列所提供的各种信息来判断是否应该终止迭代。借助不同方面的信息进行判断可否终止迭代的原则就构成了不同的终止准则。

对于一个无约束优化问题，其数值计算迭代终止准则可建立在数学分析的点列收敛的柯西准则基础上。如果按某一迭代公式所得到的点列{X^（k），k=0，1，2，…}，若有极限，即，则这点列是收敛的，且收敛于点X^*，否则是发散的。如按某一迭代公式产生的点列是收敛的，则可按此公式迭代求出最优解。

点列{X^（k），k=0，1，2，…）收敛的充分必要条件是：对于任意给定的小实数ε＞0，若存在一个自然数N，当k＞N时，满足

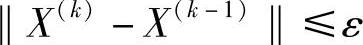
这个条件就是点列收敛的柯西准则。(www.xing528.com)

由于实际问题具有多样性，且迭代过程与目标函数的性质密切相关，所以很难建立一个统一的迭代终止准则，而是按计算中的具体情况进行判断。通常，采用如下终止准则：

（1）点距准则 相邻两迭代点X^（k）、X^（k-1）之间的距离已达到充分小，即满足

式中，ε₁是预先给定的收敛精度，取X^（k）为最优点，即

X^（k）≈X^*

或用两迭代点的坐标（设计变量）进行检验，写成

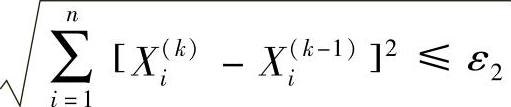
式中 n——设计维数：

ε₂——收敛精度。

（2）函数下降量准则 由于在最优点的很小邻域里函数值的变化很小，所以当相邻两迭代点的函数值下降量已达到充分小时，预示着已很接近最优点。

当|f（X^（k））|＜1时，采用函数值绝对下降量准则

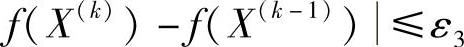
当|f（X^（k））|≥1时，采用函数值绝对下降量准则

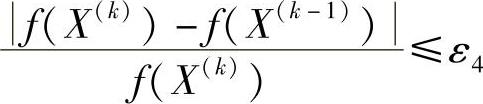
式中，ε₃、ε₄为收敛精度，取X^（k）为最优点，即X^*=X^（k）。

（3）梯度准则 按函数的极值理论，在极值点处函数的梯度为零。当目标函数在X^（k）点处的梯度的模已达到充分小，即

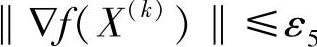
可以认为X^（k）≈X^*，ε₅是收敛精度。

上述是无约束优化问题数值迭代法的终止准则。由于无约束优化问题与约束优化问题最优解的条件不同，所以迭代终止准则有别，但以上各终止准则对约束优化的求解在有些情况下有着重要的意义。