优化设计中的性能约束条件

从7.1节中所举的几个例子表明，优化设计不仅要使所选择方案的设计指标达到最佳，同时还必须满足一些附加的设计条件，这些附加的设计条件都是对设计变量取值的限制，在优化设计中叫做约束条件。它的表现形式有两种，一种是不等式约束，即

g_u（X）≤0 u=1，2，…，m

或 g_u（X）≥0

另一种是等式约束，即

h_v（X）=0 v=1，2，…，pp＜n

式中，g_u（X）和h_v（X）分别为设计变量的函数；m和p分别表示不等式约束和等式约束的个数，而且等式约束的个数p必须小于设计变量的个数n。因为从理论上讲，存在一个等式约束就可以用它消去一个设计变量，这样便可降低优化设计问题的维数。所以，当p=n时，即可由p个方程组解得唯一的一组x₁，x₂，…，x_n值。这样，方案的选择就成为唯一的或确定的。

设计约束的形式如遇必要时也可以实现某些形式上的变化。如g（X）≤0可以变成-g（X）≥0。h（X）=0可以用h（X）≤0和-h（X）≥0两个不等式约束条件代替。

根据约束的性质不同可以将设计约束分为区域约束和性能约束两类。所谓区域约束是直接限定设计变量的取值范围，即

a_i≤x_i≤b_i （i=1，2，…，n）

此时可写成两个不等式约束，即

g₁（X）=x₁-a_i≥0(www.xing528.com)

g₂（X）=b₁-x_i≥0

所谓性能约束，是由某些必须满足的设计性能要求推导出来的约束条件。例如，设计曲柄摇杆机构时，要求满足曲柄存在条件，即曲柄为最短杆；曲柄与其他任一杆之和必小于另外两杆之和，于是可以导出其不等式约束为

不等式约束及其有关概念，在优化设计中是相当重要的。每一个不等式约束（如g_i（X）≤0）都把设计区间划分成两部分，一部分是满足该不等式约束条件的，即g（X）＜0，另一部分则不满足，即g（X）＞0。两部分的分界面叫做约束面，即由g（X）=0的点集构成。在二维设计空间中约束面是一条曲线或直线，在三维以上的设计空间中则是一个曲面或超曲面。一个优化设计问题的所有不等式约束的边界将组成一个复合约束边界，如图7-6表示了一个二维问题的可行域。其约束边界所包围的区域（图中阴影线内）是设计空间中满足所有不等式约束条件的部分，在这个区域中所选择的设计变量是允许采用的，我们称这个区域为设计可行域或简称为可行域，记作

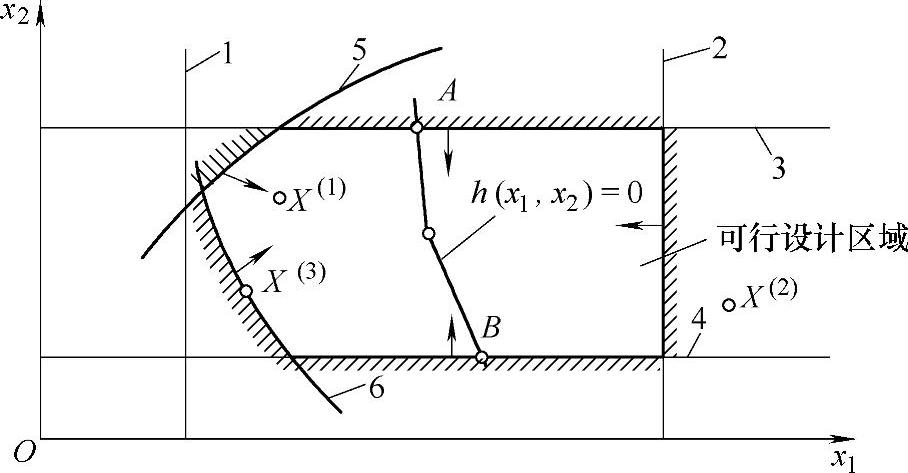
图7-6 二维问题的可行域

当某项设计除有m个不等式约束条件外，还应满足p个不等式约束条件时，即对设计变量的选择又增加了限制。例如图7-6所示，当有一个等式约束条件h（x₁，x₂=0）时，其可行设计方案只允许在ξ域内的等式约束函数曲线的AB段上选择。因此，在一般情形下，其设计可行域可表示为

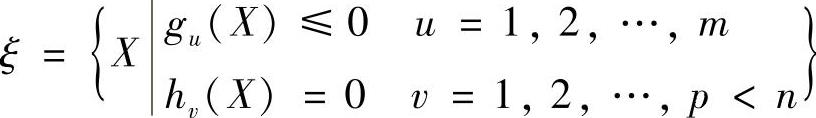
与此相反，除去可行域以外的设计空间称为非允许设计区域或简称非可行域。据此，在可行域内的任一设计点都代表了一个允许采用的设计方案，这样的点叫做可行设计点或内点，如X^（1）点；在约束边界上的点叫极限设计点或边界点，如点X^（3），此时这个边界所代表的约束叫做适时约束或起作用约束。^X（2）点则称为外点，即非可行点，该点为不允许采用的设计方案。