机械优化设计问题实例分析

在优化设计中，通常是根据分析对象的设计要求，应用有关专业的基础理论和具体技术知识进行推导来建立相应的方程或方程组。对机械类分析对象来说，主要是根据力学、机械设计基础知识和各专业机械设备的具体知识来推导方程或方程组（动力学问题中多为偏微分或常微分方程组的形式），这些方程反映结构诸参数之间的内在联系，通过它可以研究各参数对设计对象工作性能的影响。

下面通过几个具体的例子，说明机械优化设计中建立方程组的方法和步骤。

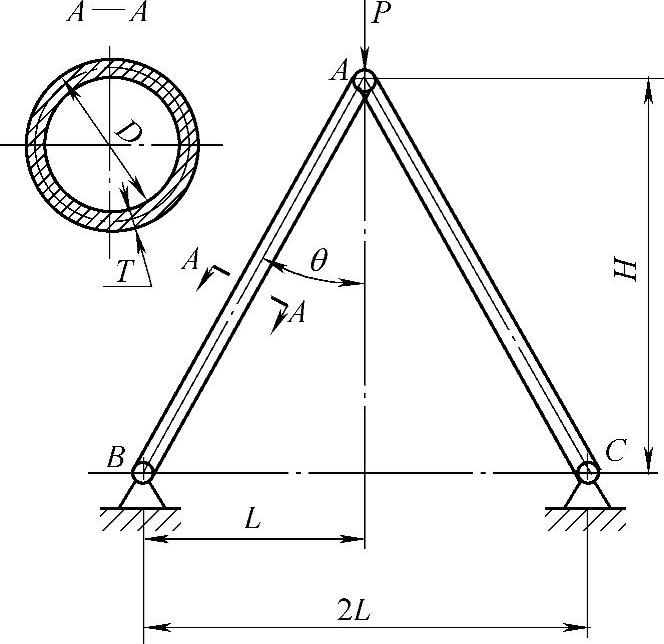
图7-1 桁架

例7-1 工程结构件优化设计

图7-1为两根钢管组成的对称桁架。点A处垂直载荷P=300000N，2L=152cm，空心钢管厚度T=0.25cm，材料弹性模量E=2.1×10⁵MPa，屈服极限σ_s=70300N/cm²。

为保证桁架可靠地工作，就必须要求杆件具有足够的抗压强度和稳定性。

抗压强度：杆件截面上产生的压应力不超过材料的屈服极限；稳定性：杆件截面上的压应力不超过压杆稳定的临界应力。

杆件由圆管制成，截面面积F=πDT

桁架为对称静定，按A点的平衡条件，得杆内力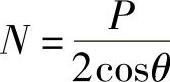

式中

杆截面压应力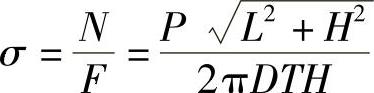

具有足够的抗压强度而不发生压缩破坏的条件为 σ≤σ_s

满足稳定性不发生屈曲破坏的条件为σ≤σ_e，σ_e为压杆屈曲极限。

按欧拉公式

式中，I为圆管的剖面惯性矩，

要求在具有足够的抗压强度和稳定性的条件下，求总体积最小的杆件尺寸参数H和d，则表达式如下：

结构总体积：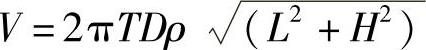

要求满足：

（1）抗压强度

（2）稳定性强度

以上所述是以D、H为设计变量的具有不等式约束优化问题。该优化问题的解如图7-2所示。

K点为最优点：d=4.7cm，H=51.31cm。

最优点的桁架体积V=686.73cm³。

图7-2 桁架最优解

例7-2 平面四连杆机构的优化设计

平面四连杆机构的设计主要是根据运动学的要求，确定其几何尺寸，以实现给定的运动规律。

图7-3 曲柄摇杆机构

图7-3所示是一个曲柄摇杆机构。图中x₁、x₂、x₃、x₄分别是曲柄AB、连杆BC、摇杆CD和机架AD的长度。φ是曲柄输入角，φ₀是摇杆输出的起始位置角。这里，规定φ₀为摇杆在右极限位置角ψ₀时的曲柄起始位置角，它们可以由x₁、x₂、x₃、x₄确定。通常设定曲柄长度x₁=1.0，而在这里x₄是给定的，并设x₄=5.0，所以只有x₂和x₃是设计变量。

设计时，可在给定最大和最小传动角的前提下，当曲柄从φ₀位置转到φ₀+90°时，要求摇杆的输出角最优地实现一个给定的运动规律f₀（φ）。例如，要求

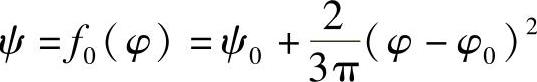
对于这样的设计问题，可以取机构的期望输出角ψ=f₀（φ）和实际输出角ψ_j=f_j（φ）的平方误差积分准则作为目标函数，使最小。

当把输入角φ取s个点进行数值计算时，它可以化约为

最小。

相应的约束条件有：

（1）曲柄与机架共线位置时的传动角（连杆BC和摇杆CD之间的夹角）

最大传动角 γ_max≤135°

最小传动角 γ_min≥45°

对本问题可以计算出

所以

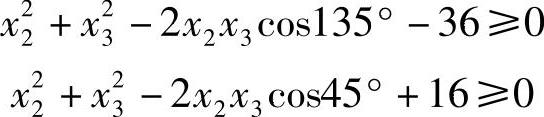
（2）曲柄存在条件

（3）边界约束 当x₁=1.0时，若给定x₄，则可求出x₂和x₃的边界值。例如，当x₄=5.0时，则有曲柄存在条件和边界值限制条件如下：

其中

1≤x₂≤7(www.xing528.com)

1≤x₃≤7

例7-3 机械零件结构参数优化

有一圆形等截面的销轴，一端固定在机架上，另一端作集中载荷P=10000N和扭矩M=100N·m，其简化模型如图7-4所示。由于结构的需要，轴的长度l不得小于8cm，已知销轴材料的许用弯曲应力[σ_w]=120MPa；许用扭剪应力[τ]=80MPa；允许挠度[f]=0.01cm；密度ρ=7.8t/m³；弹性模量E=2×10⁵MPa。现要求设计这根销轴，使其在满足使用要求下质量最轻。

图7-4 简化模型

解：这个销轴的计算模型可视为一个悬臂梁。由于设计要求是这个梁的质量，因此首先写出它的质量计算公式，即

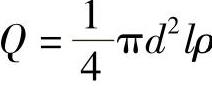
式中密度ρ是已知的。可见梁的质量取决于直径d和长度l。因此，问题就可以叙述为合理选择直径d和长度l使质量Q最小。显然，由于Q与d、l成正比，故欲Q变小必减小d和l，但是该设计还应该满足强度、刚度等各方面的使用要求，这样d和l的取值是有限制的。这些限制条件是：

（1）弯曲强度 要求悬臂梁的最大弯曲应力不得超过允许值，即

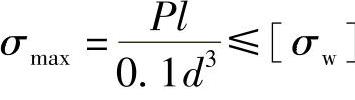
故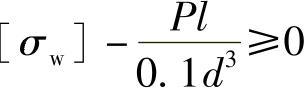

若将已知数据代入上式并经整理，则

d³-8.33l≥0

（2）扭曲强度 要求悬臂梁的扭转剪应力不得超过允许值，即

故

将已知数据代入上式并经整理，则得

d³-6.25≥0

（3）刚度 要求悬臂梁的最大挠度不得超过允许值，即

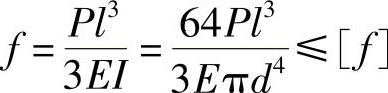
故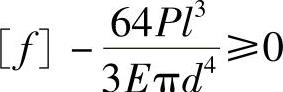

将已知数据代入上式并经整理，得

d⁴-0.34l³≥0

（4）结构尺寸 要求悬臂梁的长度不得小于给定的数值，即

l≥l_min

其中l_min为题目给定的最小长度，为8cm。故

l-8≥0

综上所述，这个问题就是要求在满足

d³-8.33l≥0 （弯曲强度条件）

d³-6.25≥0 （扭转强度条件）

d⁴-0.34l³≥0 （刚度条件）

l-8≥0 （长度的边界条件）

的条件下，选择d和l，使梁的质量

Q=0.00613d²l

最小。最优方案为d^*=4.309cm，l^*=8cm，Q=0.911kg。

例7-4 生产管理问题优化

某车间有4台机器，每台拟生产3种类型零件，每小时各零件获利润见表7-1；生产不同零件之速率示于表7-2；本月对1、2、3种零件的需求量分别为700个、500个、400个；4台机器可提供的工作时间分别为90h、75h、90h、80h。如何安排生产方可月获利最大？

表7-1 每小时生产各零件利润额 （单位：元/件）

表7-2 各机器生产零件速率 （单位：件/h）

解：为获利润最大，需合理确定每台机器生产某种零件若干。设x_ij表示第j台机器生产第i种零件的件数。

一个月内获总利润为

且要满足以下约束条件：

（1）数量需求限制

（2）工时需求限制

（3）非负条件

本题是x_ij（i=1，2，3，j=1，2，3，4）共12个设计变量的约束优化问题。