极间漏磁系数的分析及优化

目前极间漏磁系数σm的计算公式有4种，但这4种计算公式都无法准确反映极靴几何形状变化的影响，现采用“梯形积分法”，即将特殊形状的极靴划分成多个梯形后加以积分的方法，这能提高对λpb及λmb计算的客观性和准确性。

通过磁极极身的磁通　

定义空载磁极漏磁系数为σm

每极漏磁通　

式中：μ0=0.4π（亨/cm）；L为叠片长，cm；AT SZJ为消耗在气隙、定子齿、定子轭的一对极的磁势，A；∑λ为等效漏磁导系数。

式中：λmb为相邻极身内表面间的漏磁导系数；λme为相邻极身端面的漏磁导系数；λpb为相邻极靴表面间的漏磁导系数；λpe为相邻极靴端面间的漏磁导系数。

由此可见，求σm的关键在于求∑λ。

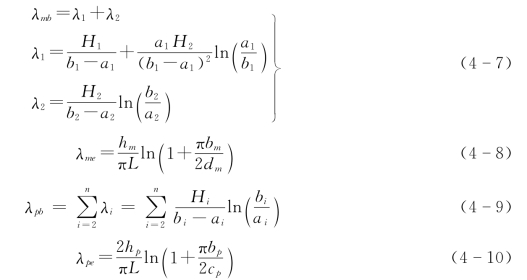(www.xing528.com)

式中：n为极间区域划分梯形的数目（不包括0号梯形），见图4-4。

在第i梯形中，H i为高，ai、bi为两底边，且规定bi＞ai，λ1对应梯形1号，即有电流部分的漏磁导系数。λ2、λ3、…、λn分别对应2号、3号、…、n号梯形，即不含电流部分的漏磁导系数。复杂极形Cp为极靴间梯形边宽的算术平均值（相重合者只取一次）。

没有特别说明的一般极形尺寸见图4-5。

用推导的“梯形积分法”式（4-3）～式（4-11）计算，结果σm值在1.314～1.34之间，对励磁电流的影响不明显，因此，在受到结构条件限制条件下的极靴尺寸还是比较合适的。

图4-4　特殊形状磁极极靴图

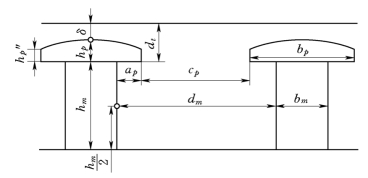
图4-5　一般形状极形尺寸