水力设计优化：转轮的设计方案

目前转轮叶片的水力设计，有升力法、奇点分布法和保角变换法，这些设计都是建立在圆柱层间无关性假设基础上，通过解一组无限平面直列叶栅来实现。

随着水轮机转轮型谱的不断完善，各水头段优秀转轮的不断投入运行，在设计转轮时，一般是采用在已有优秀转轮叶型的基础上进行优化最为便捷。因此，在优化叶型设计时，要分析的各种影响因素，特别是要分析组合叶型时的各几何参数之间关系。

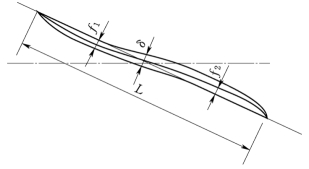
图3-23　“S”形叶片

L—叶栅长度；δ—叶型厚度；f 1—正向挠度；f 2—反向挠度

为适应正反向发电、正反向泄水和正反向水泵等六种运行工况，叶片设计成“S”形。这样，叶片只要转动45°，即可实现正反向发电、正反向泄水和正反向水泵等运行工况。由于反向发电工况的流道损失大于正向发电工况，因此其效率要低一些。

“S”叶型的首尾端互为进出口，具有双曲率的叶型中线与叶弦相交，类似两个相反方向的单向叶型连接而成，见图3-23。

3.7.2.1 “S”形叶片的动力性能

假定转轮中的水是有势流动，可将转轮的过水部分，从叶片根部ra到外缘r b沿径向分成若干个同心的流层，将叶片被分割的截面展平称为叶型，认为转轮前后的水流速度满足下列条件：

式中：r为叶型半径；V u为绝对速度圆周分量；V z为绝对速度轴向分量。

转轮旋转时，前后水流绝对速度V、相对速度W和圆周速度U应符合下列条件：

水轮机基本方程式为

式中 V u1、V u2分别为进出口绝对速度的圆周分量；g为重力加速度；H r为净水头；ηT为水轮机效率。

贯流式水轮机叶片进、出口圆周速度u=u 1=u 2

根据叶栅绕流计算转轮的功率是从有限叶型着手，并计算出由Z个叶片所组成的转轮功率。

（1）计及叶栅阻力影响的水轮机效率ηt表达式。当翼型按一定关系组成转轮叶片，并置于理想流体中时，流体力学中已证明：作用于叶型的升力P y和叶型阻力P x，可按与单个翼型类似的公式求得，见式（3-6）、式（3-7）：

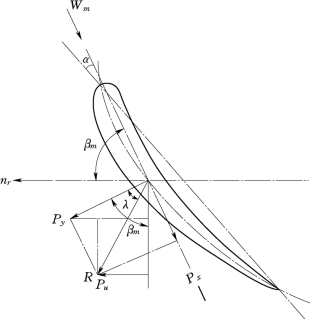
图3-24　叶型上升力Py、阻力P x 和圆周力Pu

式中：Cpy为叶型升力系数；Cpx为叶型阻力系数；为叶型进口相对流速W 1和出口相对流速W 2的几何平均值；γ为水的容度；g为重力加速度；F为叶片流体作用于叶型的面积。

dF=L·dr

式中：L为翼型翼弦长（参见图3-23）。

当水流流过微元叶片栅时，作用于微元上力R为：

式中：λ为力R与P y的夹角，见图3-24。

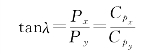
由图3-24可知，力R的圆周方向分量为P u，即

微元叶栅出力　

式中：u为转速；z为叶片数。

单元流量dQ的有效出力　

其中　

式中：t为叶片栅距；H r为水流的有效水头。

Puuz=V mzt dr

代入式（3-5）、式（3-7），得

式（3-14）是升力法设计轴流式水轮机叶型的基本方程式。

考虑水流以W m速度流经叶栅时，要克服阻力P x而引起的叶栅损失，故水轮机效率为

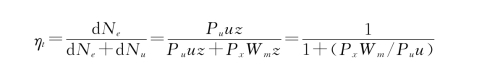
代入

Px=R sinλ

Pu=R sin（βm-λ）

得到水轮机效率：

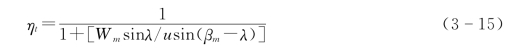
由式（3-15）可知，要设计高效率的水轮机，其叶型的冲角α和流向角βm非常重要（见图3-24）。冲角α是指无穷远处的水流方向与机翼翼弦的交角。升力系数Cpy与阻力系数C px与冲角α的关系曲线，由风洞中进行空气动力实验获得。

（2）计及叶栅阻力影响的水轮机功率表达式（不包括进出口流道损失）。当水流作用在厚度r+Δr的叶型上时所产生的功，分别为升力、阻力和圆周力，见式（3-16）～式（3-18）和图3-24。

升力：

阻力：

圆周力：

式中：Cyr为叶栅内叶型升力系数；Cxr为叶栅内叶型阻力系数；ρ为水的密度；L为叶型长度；W m为叶栅相对速度；βm为流向角。

则单个叶型的功率为

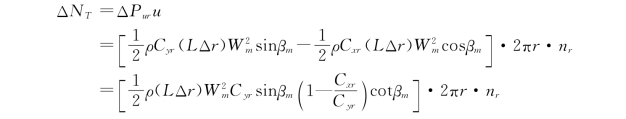(www.xing528.com)

其中

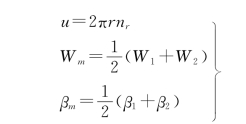
令

叶栅内叶型相对阻力系数　

叶型单位流量　ΔQ=2πr·W m·sinβm·Δr

轴向流速　V z=W m·sinβm

则通过转轮流量　

式中：Z为叶片数；ra为叶片根部半径；rb为叶片外缘半径；Cyr、Cxr、βm都与冲角α有关。因此，合理确定冲角α是非常重要的。

得出水轮机功率表达式为

式中：（1-μcotβm）称为叶栅内能量损失系数。

（3）不计入流道（包括叶片间）中任何损失的水轮机功率表达式。水在转轮室做旋转运动时，由于受重力作用，在叶片上会产生反作用力。单位质量对于单位流层的作用力，可用径向、轴向和周向分力表示，并符合如下流体力学运动方程式：

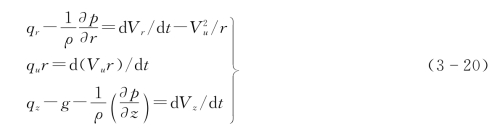
式中：V r、V u、V z分别为绝对速度在径向、周向和轴向的分量；qr、qu、qz分别为单位质量在径向、周向和轴向的作用力；r为质量作用点半径；t为时间。

水在转轮室内的流动是连续的、轴对称的，因此有

水轮机上所产生的作用力，仅是单位质量作用力的圆周分量。以功率表达形式为

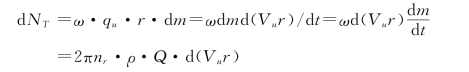
ZГ=2πr·V u代入，将上式积分得水轮机功率为

式中：m为质量；ω为角速度；ρ为水的密度；nr为每秒转速；Q为流量；Г为环量。

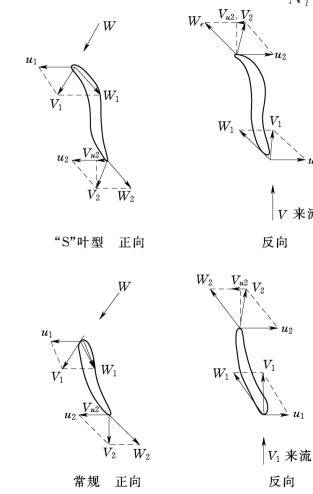
图3-25　“S”形叶片与常规叶片正反向发电时的进出口速度三角形

（4）计及全部水力损失的水轮机功率表达式（包括进出口流道损失、叶片与转轮室间隙漏水损失和叶栅内部的能量损失等），见式（3-23）。

式中：ηT为水轮机效率；γ为水的比重；Q为流量；H为水头。

比较式（3-19）、式（3-22）和式（3-23），有ZρГ·nrQ＞ZρΓnr Q（1—μcotβm）＞ηTγQH；一般情况下，ZГ=，则1-μcotβm＞ηT；令ηT=ζ（1-μcotβm），ζk=1-μcotβm

则　式中：ζ为转轮以外包括容积损失在内的综合；ζk仅是叶栅内有害阻力造成的损失系数。

由式（3-24）可知，在相同流道中（漏水损失相同）不同转轮差异是由叶片的流向角和叶栅内叶型相对阻力系数的变化引起的。

在江厦潮汐电站二期工程的“S”形叶片优化设计中，主要是调整叶片厚度δ，正、反向挠度f 1、f 2和叶片相对扭角等因素，使水轮机的性能有所提高。

3.7.2.2 “S”形叶片设计

“S”形叶片与常规叶片正反向发电时的水轮机进出口速度三角形如图3-25所示。

由图3-25可知：“S”形叶片与常规叶片的进出口速度三角形是不一样的。反向发电时，正向来流，且导水机构全打开，ζ值比正向发电时小，影响ζk的μ、βm在同工况时反向发电时的βm总比正向发电时小（Vu1=0），故反向效率总低于正向。

另外，常规叶片要满足Vz为90°出口或略带Vu2出口还是可以做到的，但“S”形叶片则难做到。所以，“S”形叶片设计要考虑正反向发电的效率，也就是要适当选择挠度f1、f2值。

试验结果表明，f＜2.5%时能有效地转换能量。如将f2减小，并使δmax所在位置靠近正向水轮机的进口端，可提高正向水轮机的效率，反向水轮机效率有所下降。但由于相对挠度减少，使运行稳定性增强。

试验表明：叶片相对扭角由25.5°增至30°时，单位流量可提高较多，但水轮机效率却下降7%～8%，因此叶片相对扭角不宜过大。

图3-26　“S”形叶片转轮

在反向水轮机工况中，转轮来流可视为轴向来流，进口环量Г1=0，此时出口环量Г2＜0时才能满足水轮机做功的要求。这只有反“S” 叶型才能满足这个要求。但反“S”叶型在正向水轮机工况中会引起冲角过大而使效率下降。

“S”叶型在试验中曾出现过两种情况：一是重复性差；二是不稳定。其主要原因就是由于叶片相对挠度过大，在叶片末端产生脱流引起压力脉动所致，减少叶片相对挠度，可提高转轮的能量指标，并可改善运行稳定性。图3-26为“S”形叶片的转轮。

表3-8为不同方案叶型主要参数，表3-9为正反向发电模型试验结果。

表3-8　不同方案叶型主要参数

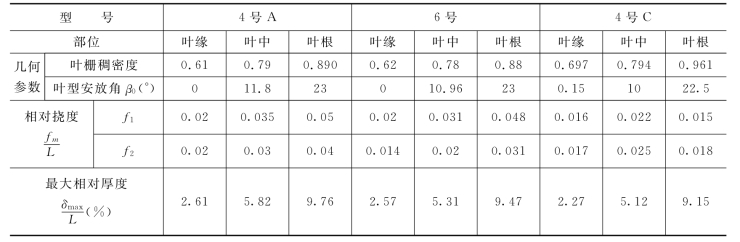
表3-9　不同方案正反向发电模型试验结果

由表3-8、表3-9可知，6号与4号A比，6号f 2减少，且位置靠近正向水轮机进口端，给反向水轮机造成收缩的栅内流道，因此反向效率显著下降，正向效率提高，但由于相对挠度减小，运行稳定性也较4号A为好。

4C方案为综合各方案优点而设计的，叶栅稠密度的增加没有减少单位流量和单位转速，得到了较佳的能量指标，且各工况点的稳定性都达到了设计要求，成为推荐方案，即F03转轮。

转轮叶片参数选择是相互关联的，相对扭角（直接涉及冲角）在双向叶片设计中占有特殊地位，如取值不当出现负冲角或冲角过大时都会严重影响转轮的水力性能，甚至影响机组稳定运行。一般正向冲角变化为7°～8°，反向为0.5°～6.5°。

要得到正、反向水轮机工况性能均较佳的叶型，可采用叶片周边截面采用正“S”叶型，而在轮毂处采用反“S”叶型。这种叶型组合可大大提高反向水轮机的效率，可使正向水轮机性能得到改善。也可避免由于采用正“S”叶型在出水边附近可能出现的脱流现象，这对于改善汽蚀性能也是有利的。

3.7.2.3 水泵的功率表达式

仅计及叶栅内能量损失的功率为

N p=ZρГnrQ（1+μcotβm）

计及全部损失的功率为

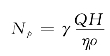
令　　　ζk=1+μcotβm ηp=ζ/ζk

则　　　N p=γQH（ζk/ζ）

式中：ζk为叶栅内阻力损失系数；ζ为流道内阻力损失系数；H为水泵扬程；Q为流量；ηp为泵效率。

对于对称叶型双向水泵，ζk近似相等，但ζ变化较大；对于从水库向海水泵（反向水泵），水流阻力小，其效率略高于正向水泵。