空间是流动、转换的。空间不仅能转换到另一个空间里去,还能径自衍变出其它的空间(图5-78),空间不应该被“形”所捆绑,用形的角度界定空间是思维的一个偏见。这时,维度是一个很重要的空间概念。服装造型语境中的多维空间的挖掘,是原创的结果,也离不开数的支撑。也就是说,数来源于形,因此能把形还原出来,这种“数形结合”的理念,不但对理解空间、维度有重要的意义,而且有助于造型与数字化之间的转换。创意立裁拓展出的多维空间,并不局限在某一个空间上的概念,这种逻辑推演是理性思维中的内容,也能在艺术上获得感应,成为对结构状态的大胆设想,它们超越了诸如比例、尺度、角度的一般形态。空间就是四维的。它所具有的拓扑维度把我们从三维静态空间引向了动感、模糊、矛盾、循环、延续、拓展等空间特性中。


图5-79
1.拓扑结构造型
拓扑结构来自拓扑几何。拓扑几何是一种能变形的、动态的几何体系,它允许一个形体在保持不出现撕裂和裂缝的情况下,以各种可能的方式接受所有可能的变形,这种连续性变形称为拓扑变形。拓补学不研究长度、角度等细节,而是研究形式的基本构成方式以及物体连续、闭合等结构性质。在拓扑几何的语言中,在运动中形的大小和形状都在发生变化。拓扑几何的结构造型瓦解了欧几里得几何形态的静止的、确定的形态,呈现出动态的效果。拓扑对循环的强调也使得拓扑空间常以扭曲、连续的形式存在,并伴随有一定的矛盾性。
让一个平面进行首尾旋转的结合,使之形成没有里外之分的循环态势,这种二维面的交叉形式称之为“梅比斯环”(图5-79)它是拓扑理念下的三维体。两个“梅比斯环”即能合成一个“克莱因瓶”;把“克莱因瓶”从中间切开,又能产生两个“梅比斯环”。这种复杂的维度转换,让人们看到“空间”概念中所蕴含的多层次的内容(图5-80)。

图5-80
曲线(或直线)和二维(曲面)就可描绘出多维(n维)空间的独特魅力。这对于我们重新梳理基础的造型语言有着直观的理解作用,其实面料(二维)本身就潜藏着空间转换的可能(图5-81)。简单的线与面能随境而生,从可见的线、面,可以延伸到无形而又无限的空间中。二维既可以生出三维,也可以直接创造出四维甚至更多的维度。
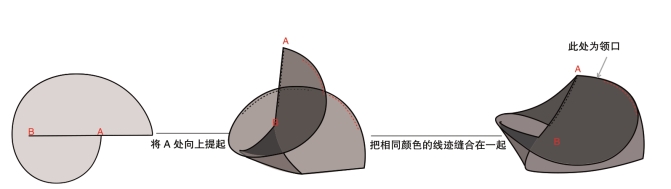
图5-81
拓扑空间的维度意识,让我们得以改变一般的经典几何体(如服装上的A形、H型、O型)在人身上形成的僵硬、刻板的状态。拓扑是可转化的空间关系:在一个具有足够的量的正方形体积上施加各种形式的力(穿插、旋转、折叠等),都能使之变为一个“圆”或“圆锥”体的形态。这种变形过程不是静态的,它是动态的,是一个连续的变化过程(图5-82~图5-85)。在动态与连续中,已含有时间的概念。在三维上加入“时间轴”,即构成了我们所说的“四维”概念,它超越了静态的三维评价体系。在现代服装结构中,对经典板型的应用都是在静态的三维空间意识中进行的,每一条线、每一个空间都被赋予了规定的含义。
在创意立裁的“互动”中,由于融入了拓扑理念,使设计者不拘泥于现有形式,每条线、每个空间、每个细节都能循环、转换。

图5-82

图5-83
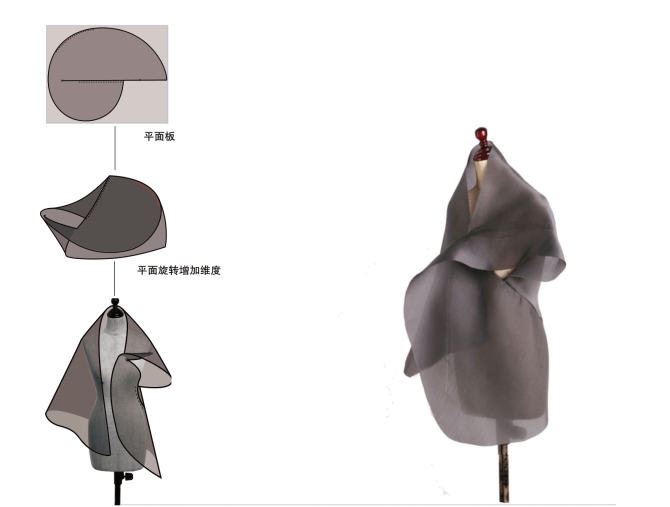
图5-84
依据平面板型在立裁旋转造型

图5-85

图5-86
由此形成的“拓扑互动”是“创意立裁”中的特色部分。拓扑空间以接近于“无形”的境界让我们在创意立裁的互动中拥有“无限”的空间与形态。不管用何种手法操作,拓扑造型思维下的衣、袖、领、前后衣片、上下衣身,都将呈现出连接、循环、转换、矛盾等空间形式(图5-86~图5-97)。

图5-87

图5-88
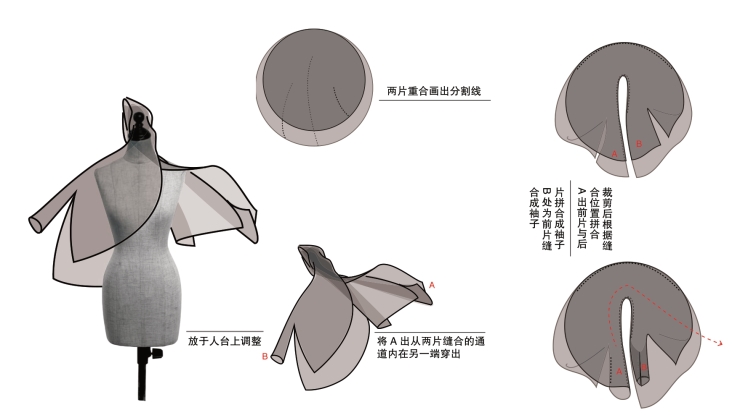
图5-89

图5-90

图5-91
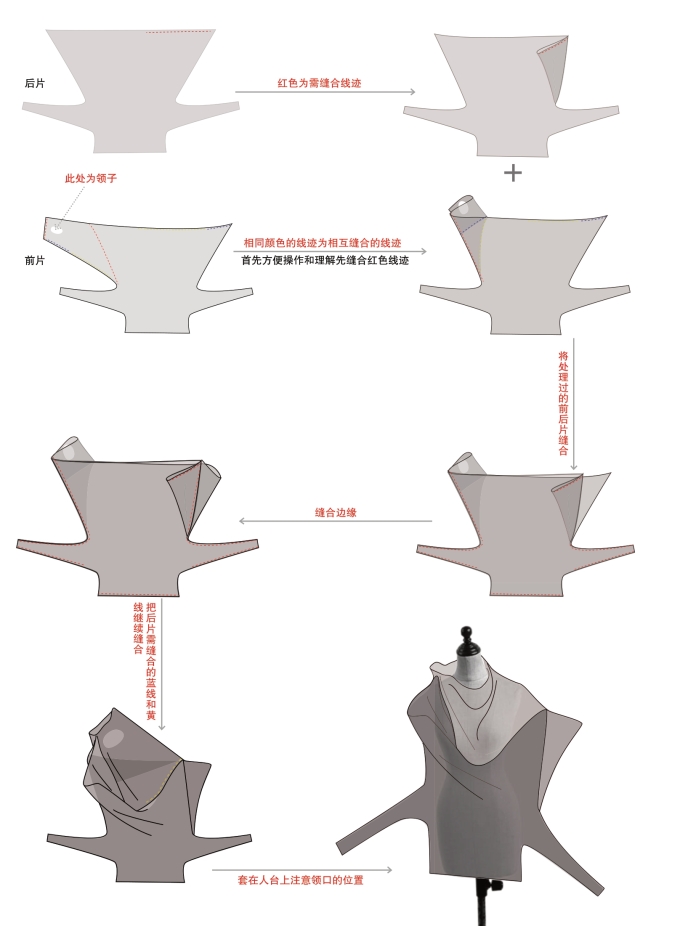
图5-92

图5-93

图5-94

图5-95

图5-96
建筑师格雷格·林恩认为,拓扑曲面固有的弯曲性表现了将不同问题进行整合的逻辑;拓扑曲面依靠向量描述,因此它们可以系统地将时间因素和运动因素的影响表达在形态之上。(https://www.xing528.com)

图5-97
2.分形结构造型
分形结构来自于分形几何。分形几何的概念由曼德布罗特1975年提出,它是探索和处理自然与工程中不规则图形的理论工具。分形几何的基本思想是:客观事物具有自相似的层次结构,局部与整体在形态、功能、空间等方面具自相似性。可以将其简单理解为一个粗糙或零碎的几何形状可以分成多个部分,且每一部分都(至少近似地)是整体缩小后的形状。分形几何在任意小的尺度上都能有精细的结构,并且其结构往往呈现出明显的秩序性和渐变感。实际上自然界中没有真正的分形,但服装造型设计可以利用事物的自相似性进行几何的分形。
“分形”可以简单地理解为“某个简单的几何形状可以分成多个结构近似的部分”。利用分形几何概念以及维度空间的量能转换,对于创意立裁有着直接的借鉴价值。分形是以“非整数维”的形式充填空间的形态,来表达一个动态的变化过程。相似性是它最基本的特征,具有一定的秩序感。
分形形态使我们改变了用孤立的眼光看待事物中点、线、面的思维习惯,而是把它们视为一个整体形的产物,点线面是从形中分离出来的,而不是用点线面去“造形”。这些特有的形态,是可以用数学、物理的方式有系统、有逻辑地加以运算和描述。运算的结果让我们看到原本无法“看到”的惊人细节(包括空间结构):它们以相似的“层次”结构,使事物细化至无穷的层次。适当的放大或缩小,并不能改变它的尺寸和结构。这种由数学运算出的复杂形态,为人们增添了新的审美追求和审美对象。
在创意立裁中引入分形理念,可以让一个立体几何随着分形次数的递增而逐渐分解,从而转化成另一种形态,同时又保持了原结构的相似性。它们由局部出发延伸至整体。在分形造型形态中,整体常常反映出局部的特征,或者说,整体是由局部的特征构成的。
分形造型可分从以下两类入手:一是几何分形,它不断地重复同一种形态或图案;几何分形常呈现出多个几何体的相交或相嵌,以此拓展出的空间维度造成强烈的空间感受。另一种是随机分形,包括用计算机依靠迭代生成的方法,创造出奇异而混沌的图形。在创意立裁中,我们也可以进行类似的分割,无疑会为设计者扩展出新的自由空间,它超出了以人的主观审美和寓意为触发点的创作模式,让人得以进入纯粹的形式情景中去。
(1)圆柱分形
在以圆柱体为分形的基础体上,先在圆柱中央位置挖两个开口,其大小分别能适应于颈部以及臀部大小。将圆柱简单地分割,然后套在人台上(图5-98)。
用其他分割形式进行分割,并观察圆柱分割完成后呈现出的分形自相似性。在随机的操作中发觉它的形态可塑性,再置于人台上调整造型(图5-99)。
参照下面的图例(图5~100~图5-102),用面料展开款式造型。

图5-98
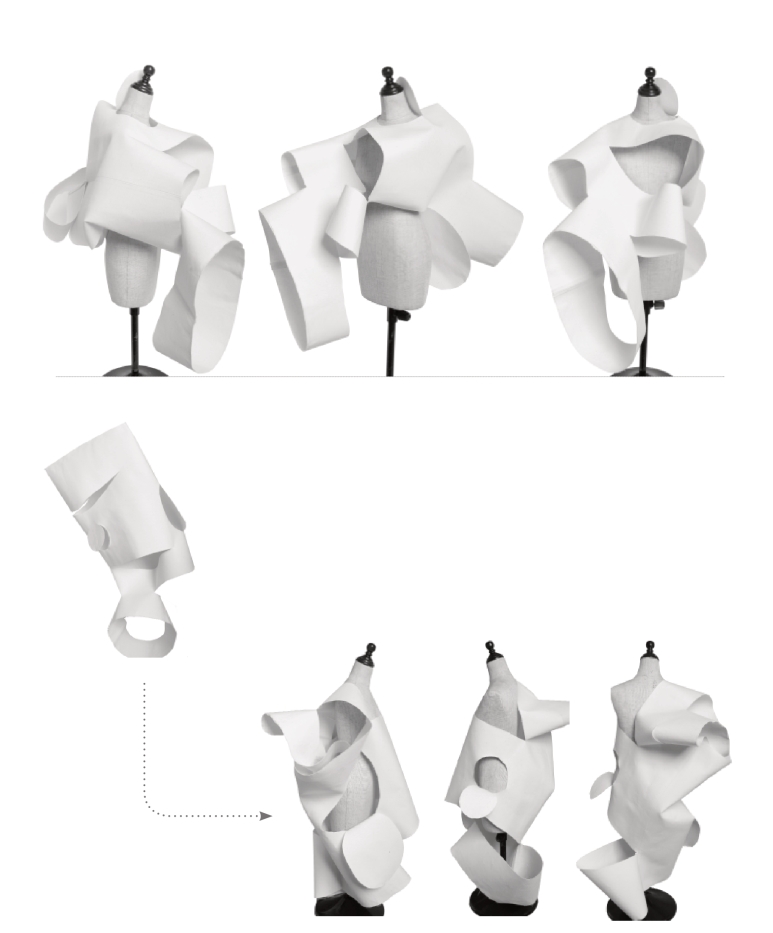
图5-99

图5-100

图5-101

图5-102
(2)锥体分形(图5-103)
在锥体基础上只分割一刀,套置于人台上,观察到锥体被分割成两个非常明确的相似锥型分形空间,然后依据此形态进行服装在人体上的造型尝试。
在同样的锥体上随机分割两刀或三刀,使锥体自身形态与分形语言互溶。参照图5-105的造型互动形式,摆脱了锥体与人体近似形态的拘泥,呈现出分形语言自身带来的超乎想象的空间形态。选择各种形态与人体互动,以诱发更多的造型可能。

图5-103

图5-104
(3)锥体分形拓展
做一锥体基本型,可直接放在人台上做随机分形,一边观察分形完成的连续、分叉及缠绕的几何形态,一边进行造型发散。先将一块正方形布的两个邻近边缝合构造成锥体(去掉顶角),然后在锥体上随机分形。由于分割线的数量、形状可变性与立体几何形态的灵活度相结合,可产生无穷尽的多样分形空间。
选择一种分形空间形态并与人体互动,将有灵感的秩序部分进行拓展,是不断完善服装创造语境的过程(图5-105、图5-106)。

图5-105
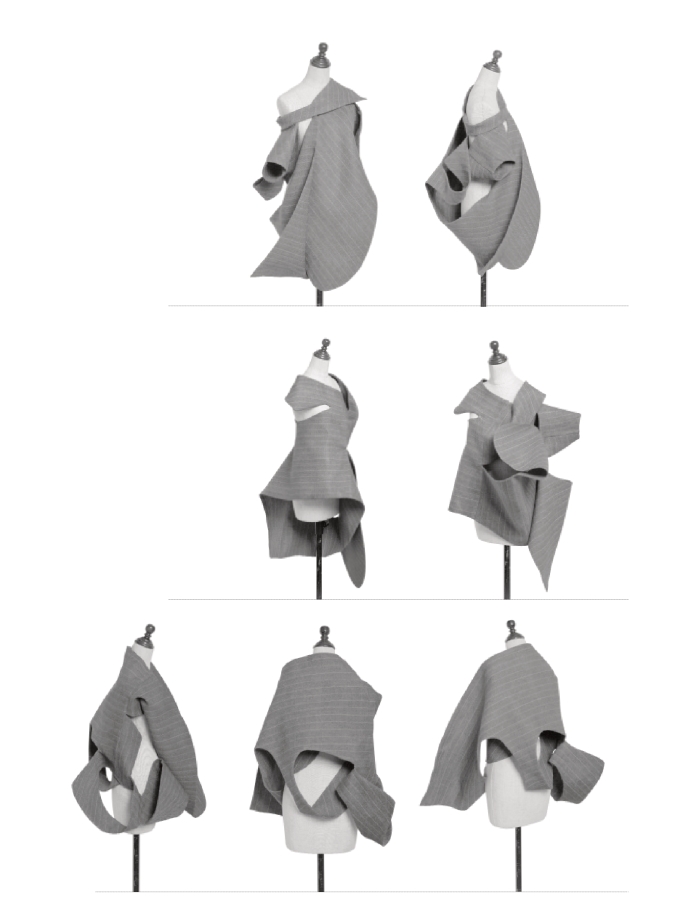
图5-106
“分形”似乎具有一定的衍生性,它能将某一个局部切割、组合出丰富的维度效果。但实际上,分形是维度的分数化,是非整数的维度(例如2.5维),看来分形空间还难以被列入多维空间的范畴。但分形毕竟以它独特的形式,让我们意识到空间的维度是可以从整数维拓展到分数维的。从计算机推算出来的分形空间上可以看到:分形产生的空间造型是人类思维所难以想象的。下面的图例(图5-107~图5-110)是依据分形造型方法进行的款式造型尝试。

图5-107

图5-108

图5-109

图5-110
从个人的角度理解“空间”内涵,很大程度上包含着一些尝试因素。当尝试着用理性思考和感性审美相结合的方法建立起创意立裁的“技术与艺术结合训练体系”,意味着立意裁剪不仅限于技术层面的突破,许多创意元素正等候着“入场”的时机。深度的思考确实离不开理性(包括逻辑)的支持,在本章中,我对一些司空见惯的概念重新进行了梳理,这对创意立裁具有特殊的意义。为此,我甘愿冒着“偏颇”、“歧义”的风险,仅供抛砖引玉。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




