装配尺寸链计算的方法与步骤

装配尺寸链的应用包括两个方面：其一，是在已有产品装配图和全部零件图的情况下，由已知的组成环的基本尺寸、公差及偏差，求封闭环的基本尺寸、公差及偏差。然后与已知条件相比，看是否满足装配精度的要求，验证组成环的基本尺寸、公差及偏差确定得是否合理。这种应用称为“正计算”；其二，在产品设计阶段，根据产品装配精度要求（封闭环），确定组成环的基本尺寸、公差及偏差，然后将这些已确定的基本尺寸、公差和偏差标注到零件图上，这种应用方法称“反计算”。但无论哪一种应用方法，装配尺寸链的计算方法只有两种，即极值法和概率法。概率法解算尺寸链的步骤如下：

1.各环公差的计算

根据概率论的原理，即独立随机变量之和的均方根误差σ0与这些随机变量相应的σi值有如下的关系

在装配尺寸链中，其组成环（即各零件加工尺寸的数值）是彼此独立的随机变量，因此作为组成环合成量的封闭环也是一个随机变量。

当尺寸链中各组成环的尺寸误差都遵循正态分布规律，则其封闭环也将遵循正态分布规律。此时各尺寸的随机误差，即尺寸的分布范围为其均方根的6倍。

令尺寸的公差T=6σ，则封闭环公差T0与各组成环公差的关系式为

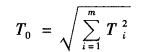
即当各组成环公差都为正态分布时，封闭环的公差等于各组成环公差平方和的平方根。

如零件尺寸不属于正态分布时，则上式需引入一个相对分布系数k，则有

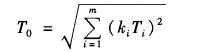
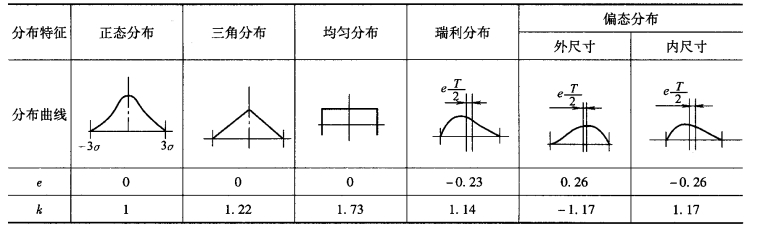
不同分布曲线的相对分布系数k值见表6-1。

表6-1　一些尺寸分布曲线的k和e值(www.xing528.com)

2.各环算术平均值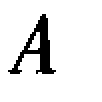的计算

根据概率论原理，各环的基本尺寸是以尺寸分布的集中位置即用算术平均值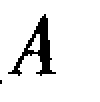来表示的，所以在装配尺寸链中有

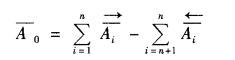
即封闭环的算术平均值等于各增环算术平均值之和减去各减环算术平均值之和。

当各组成环的尺寸分布曲线属于对称分布，而且分布中心与公差带中心重合时，见图6-8a，则其各环的算术平均值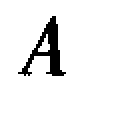即等于该尺寸公差带的中心尺寸（称之为平均尺寸Aav）。此外亦有

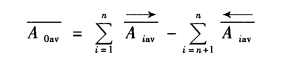
图6-8　分布曲线尺寸的计算

a）对称分布　b）不对称分布

按以上计算出各环的公差以及各环的平均尺寸Aav后，各环的公差对平均尺寸应注成双向对称分布，然后根据需要，可再改注为具有基本尺寸和相应的上、下偏差的形式。

利用概率法时，需要掌握各组成环的尺寸分布规律，即已知相对分布系数k及相对不对称系数e。在缺乏这些统计系数时，可假定e=0，k=1.5进行近似估算。由于概率法在计算上的复杂性，所以它在应用上受到一定限制。