哈瑞立刻打开ISO和ASME的标准，发现的确是四大公差，见表3-1。
表 3-1
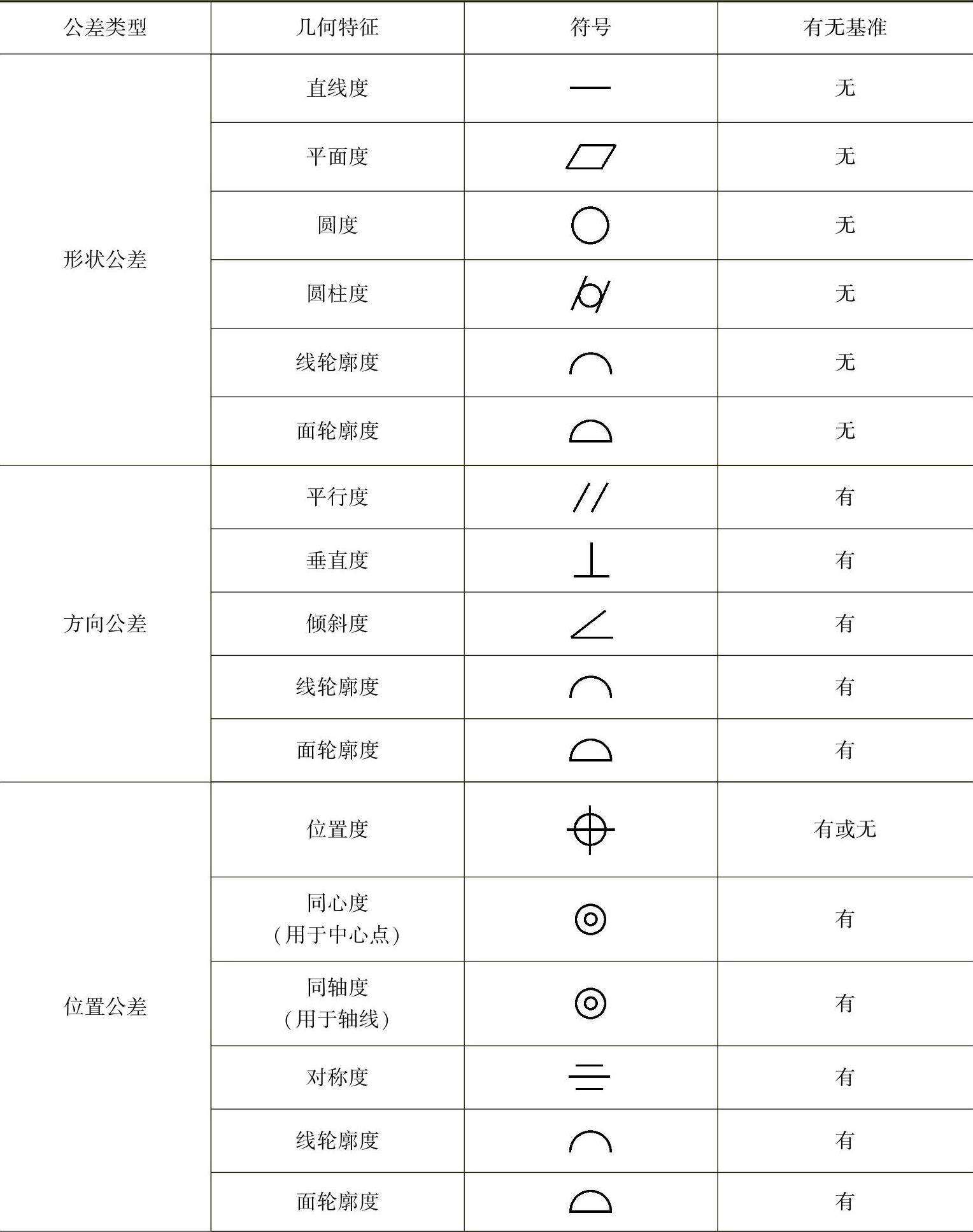
（续）
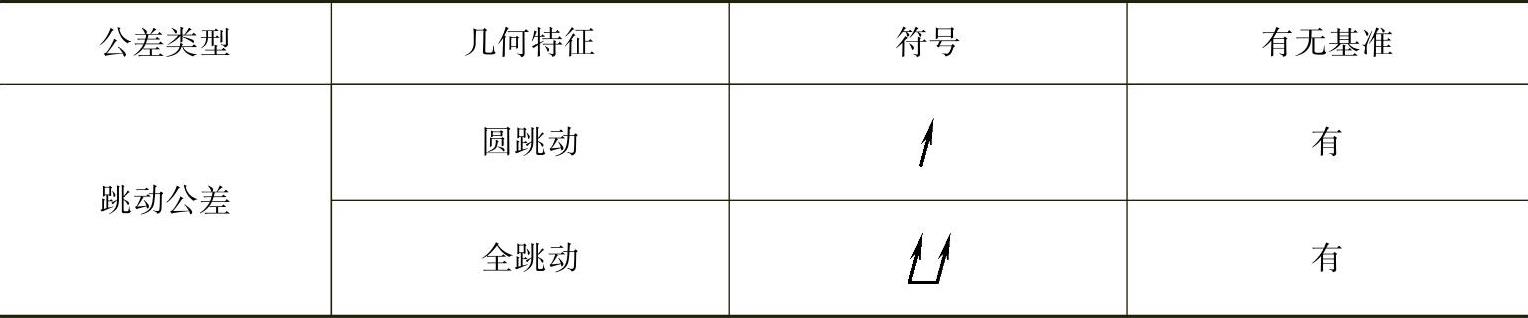
躺在宿舍的哈瑞又进入了梦乡，再次见到了火星来的测量员同事，他正在测一张桌子是否合格。这次的测法是正确的，把桌腿放在大理石平台上，用三坐标测量机CMM测头测桌子表面。几分钟后，三坐标测量机CMM将桌面的测量点模拟出一条曲线（图3-18），火星的同事在曲线上画出了几条平行线（图3-19），这几条线引起了哈瑞的好奇。
图 3-18
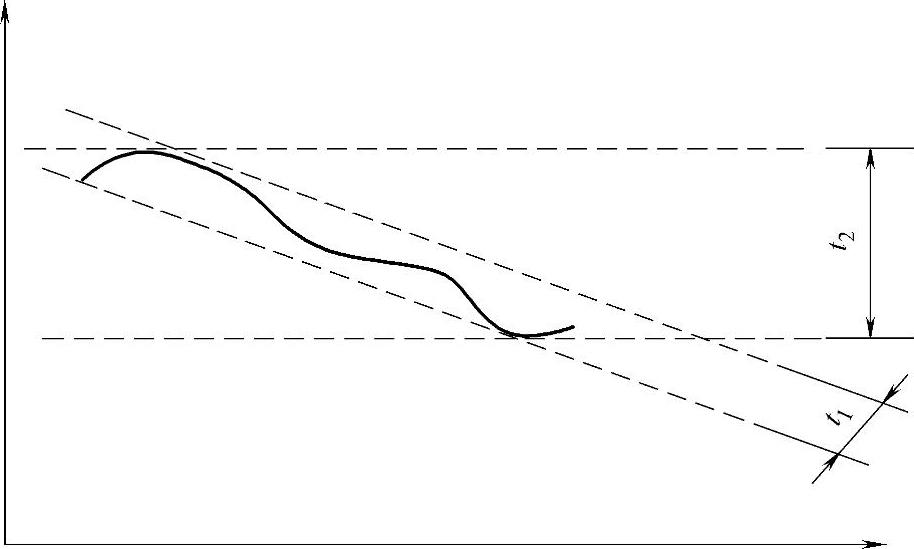
图 3-19
火星同事解释道：“两水平虚线间的距离t2是相对于地面的平行度值。两倾斜虚线间的距离t1是平面度值。”
哈瑞：“如果桌面逆时针旋转摆正（图3-20），则平行度和平面度正好相等，如果桌面稍斜一点，平行度报告上升，而平面度报告不变，对吗？”
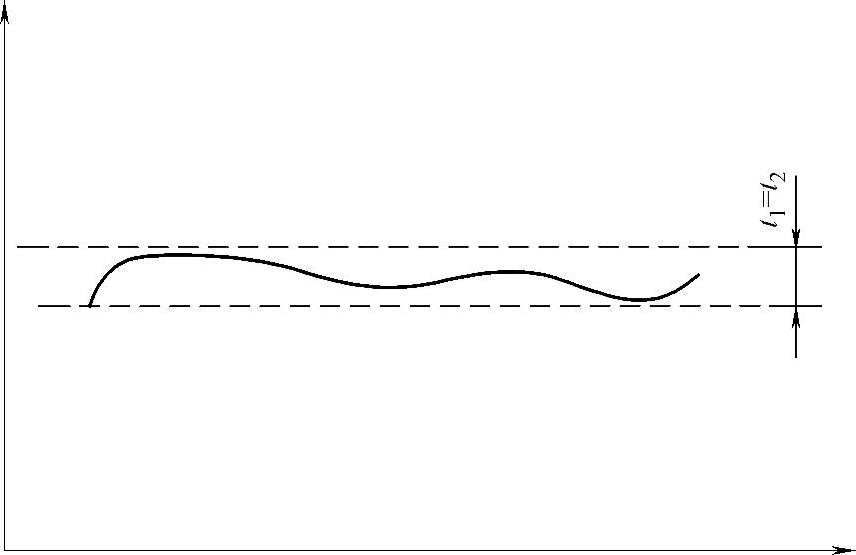
图 3-20
火星同事：“有道理，但没人这样想过，这样想有什么意义呢？”
哈瑞：“意义很大，当桌面平行度报告为1mm时平面度必然小于或等于1mm，也就是说如果对桌面提出1mm的平行度要求，那么实际上也控制了桌面的平面度在1mm以内。”
说完画了个表格（表3-2）。
表 3-2 （单位：mm）
(www.xing528.com)
这时火星同事拿出一张表来，说：“我师父给了我一张类似的表格（表3-3），我没看懂。”
表 3-3
（续）
哈瑞看到这张表，茅塞顿开，“如果我们对桌面高度要求是在100～120mm之间，桌面的平行度就不可能超过10mm，同时桌面的平面度也不会超过10mm。”然后他拿着这张表就去找天佑，一个健步，哐当一声摔下了床，才知道自己是在做梦。
爬上床一想，那跳动呢？跳动是如何控制位置、方向和形状的呢？想着想着又进入了梦乡。回到大学校园，哲波老师正在指导大家做毕业设计，微笑着说道：“同学们，几何公差不知道标什么时，请标跳动，因为跳动对形状、位置、方向都能管控……”
在哲波老师风趣的话语中，下课铃响了，天也亮了，原来是闹铃响了。翻开大学的笔记本，四个经典图形出现在眼前（图3-21、图3-22、图3-23、图3-24）。
哈瑞立刻复习了一下所有几何公差的公差带。
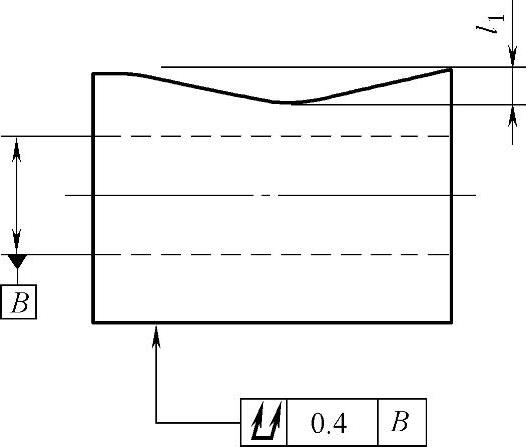
图 3-21
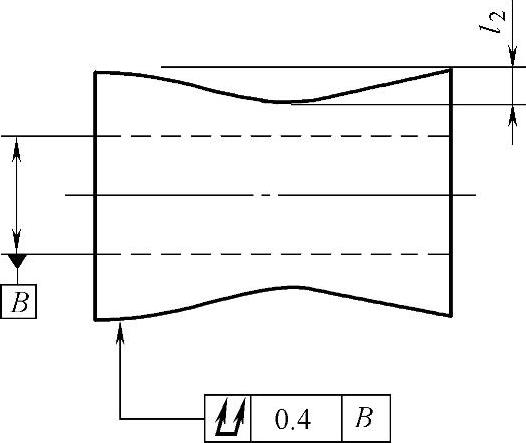
图 3-22
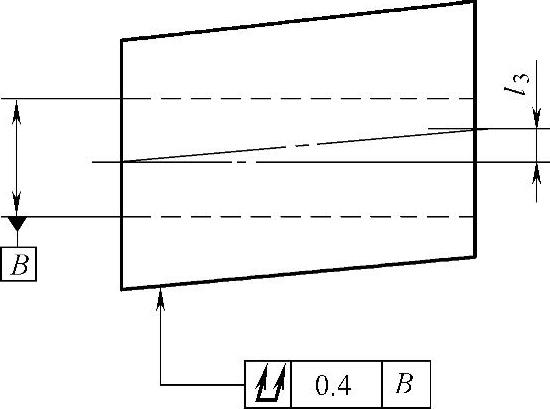
图 3-23
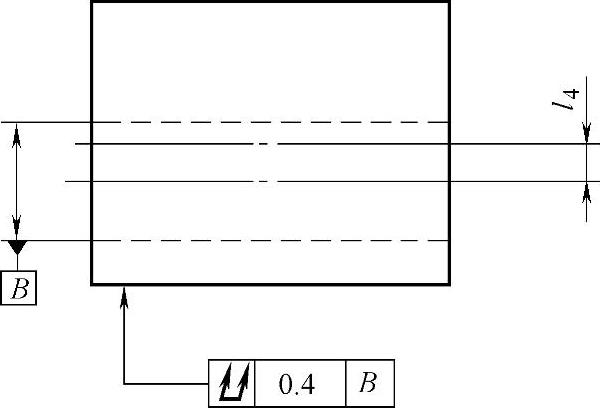
图 3-24
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
