如何计算质数等分数的分度值？

当工件等分数Z为质数，不能进行因子分解，如19、31、47等，或者利用公式（N∶1=40∶1=n∶）不能进行分度（如63、87等）时，就要使用新的方法进行分度，常用的方法有差动分度法和单动间隔分度法。

1.差动分度法原理及其计算

差动分度就是在分度头主轴的后锥孔和侧轴处安装交换齿轮，如图4-3所示，分度时摇转分度头摇柄，带动分度盘顺时针或逆时针一起转动，利用摇柄和分度盘之间的相对运动实现分度。

图4-4中，若不采用差动分度，摇柄从1转到2的位置，应转过的转数为X₁。若采用差动分度，分度盘随着摇柄转动，分度盘转数为Y。分度盘和摇柄转动方向相同时，摇柄实际转数X=X₁+Y，如图4-4a所示；两者转动方向相反时，X=X₁−Y，如图4-4b所示。

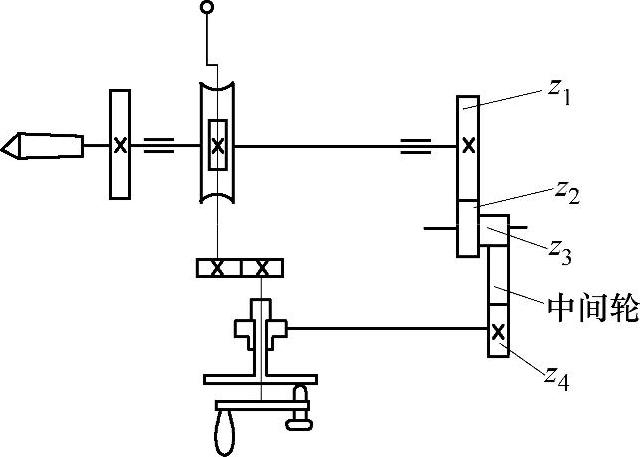
图4-3 差动分度传动系统

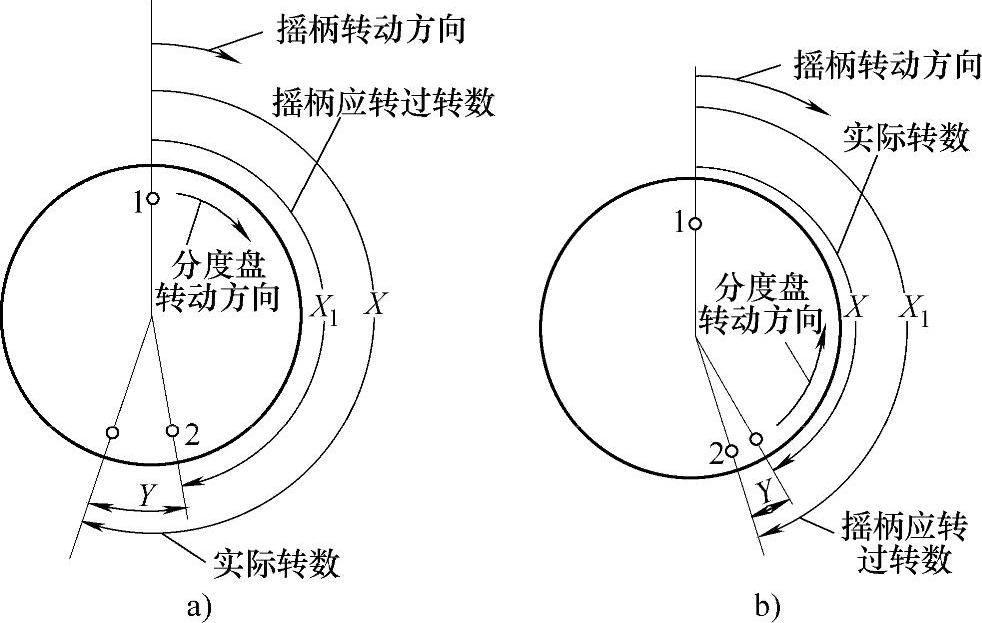
图4-4 差动分度中的摇柄和分度盘

a）转动方向相同 b）转动方向相反

差动分度可按以下步骤进行∶

1）选定一个假定等分数Z₀。

2）按照假定等分数Z₀计算分度摇柄差动转数n₀，即

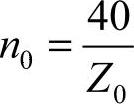
3）确定交换齿轮z₁、z₂、z₃、z₄的传动比i，。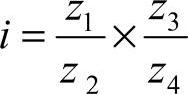

差动分度中，由于交换齿轮的作用，分度盘和摇柄差动转动，这时的分度盘转数n′等于分度摇柄应转过的转数减去分度摇柄的差动转数n₀，即n′=n−n₀，亦即

由于操作中每分度一次，分度头主轴就转1/Z转，工件和分度头主轴属同一轴上，这时

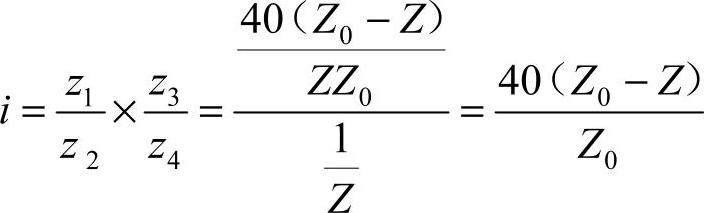
差动分度中，若Z₀＞Z，i为正值，这时摇柄转动方向和分度盘转动方向相同；若Z₀＜Z，i为负值，摇柄转动方向和分度盘转动方向相反。两者的转动方向可通过增加或减少中间轮来实现（中间轮不会改变传动比i）。

根据式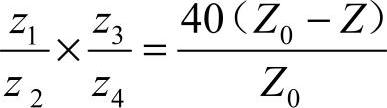，设Z₀−Z=X，则得

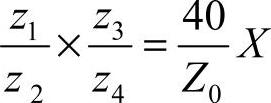(www.xing528.com)

由于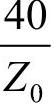=n₀，于是有

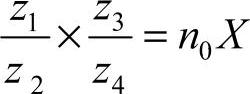
差动分度的计算应以下式进行验算，验算出的等分数应与要铣削等分数相等，否则计算有误。

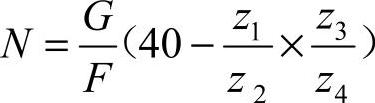
分度摇柄转动方向与分度盘转动方向相反时用下式验算

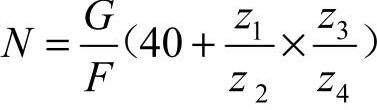
式中 N——验算出的等分数；

G——分度中选定的孔圈数；

F——每次分度摇柄转过的孔距数。

2.单动间隔分度的原理及其计算

差动分度法可以精确地解决所有不能进行因子分解的质数等分数的分度，但不能应用于铣削锥齿轮和斜齿圆柱齿轮，此时只能采用单动间隔分度法。

单动间隔分度法是一种带有误差的分度方法，所以也称近似分度法，可以应用于一般齿轮的加工。

单动间隔分度时，设分度头速比为40∶1，工件等分数为Z，选择分度盘孔圈数为N，则有

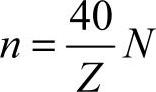
其中，40/Z对于分度的工件来说是个常数，所以n随N而变。对于不能进行因子分解的质数，用40/Z不能分度的根本原因就在于选择任何孔数N都不能约去分母，不能使n成为整数，即n总是小数。这时，可以乘上一个整数m，使这小数变成或者接近一个整数，然后取这个接近的整数来进行分度，即

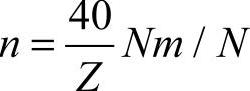
式中 n——分度摇柄转数；

Z——工件等分数；

N——选取的分度盘每圈孔数；

m——铣齿分度间隔齿数。