尺寸链解算实例及简图分析

例1-1加工图1-18a所示轴承座，设计尺寸为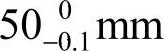和。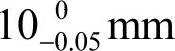

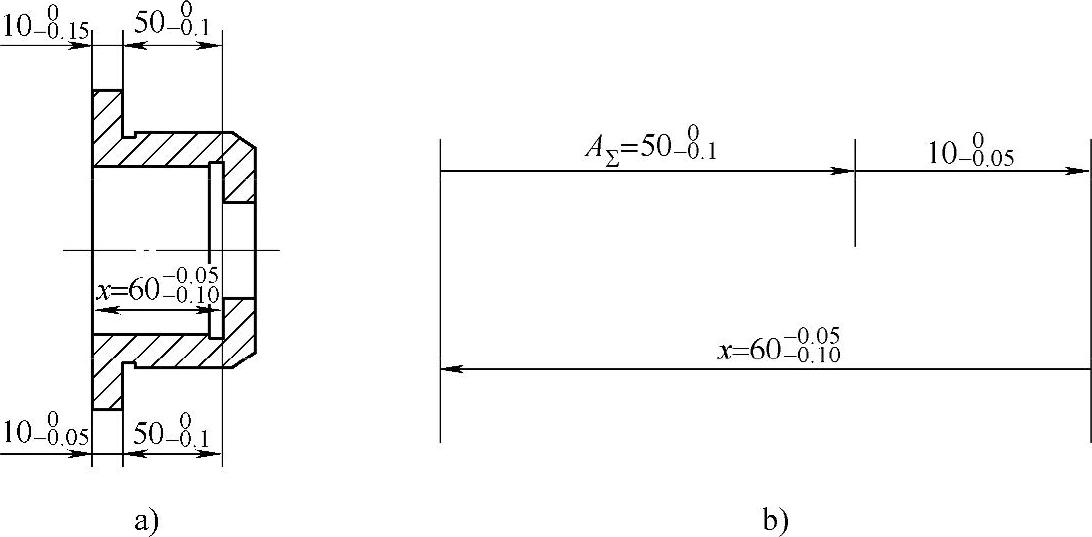
图1-18 轴承座

解 由于设计尺寸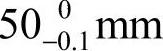在加工时无法直接测量，只好通过测量尺寸x来间接保证它。尺寸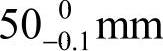、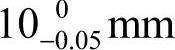和x就形成了一工艺尺寸链。分析该尺寸链可知，尺寸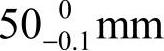为封闭环，尺寸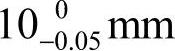为减环，x为增环。

利用尺寸链的解算公式可知

因此，。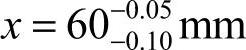

尺寸链图如图1-18b所示。

计算上面的尺寸链，由于环数少，利用尺寸链解算公式比较简便。不过，公式记忆起来有的人会感到有些困难，甚至容易弄混；如果尺寸链环数很多，利用尺寸链解算公式计算起来还会感到比较麻烦，并且容易出错。下面介绍利用竖式解算尺寸链的方法。

利用竖式解算尺寸链时，必须用一句口诀对增环、减环的上、下极限偏差进行处理。这句口诀是：“增环上、下极限偏差照抄，减环上、下极限偏差对调并反号”。本例将该尺寸链列竖式则为

同样解得(www.xing528.com)

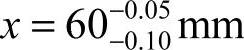
例1-2加工图1-19a所示零件，A、B、C面在镗孔前已经过加工，镗孔时，为方便工件装夹，选择A面为定位基准来进行加工，而孔的设计基准为C面。

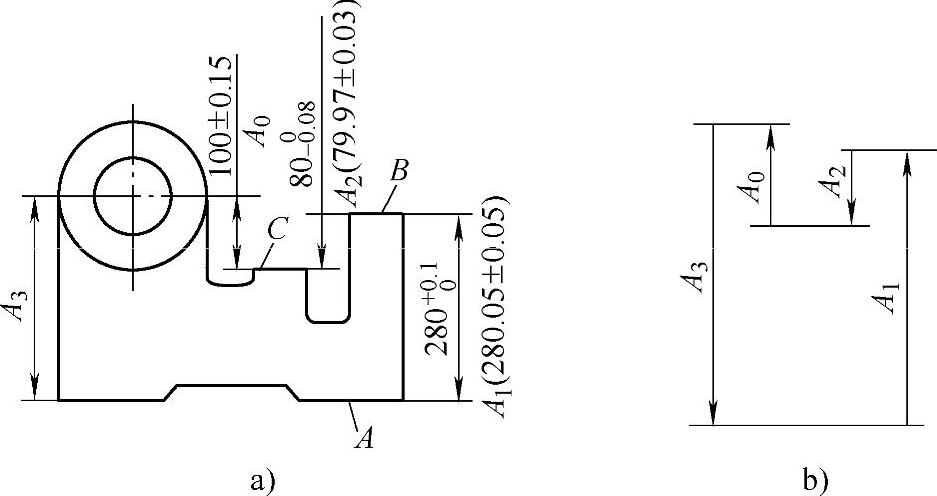
图1-19 零件图及尺寸链简图

解 显然，此属于定位基准与设计基准不重合，加工时镗刀需按定位基准A面来进行调整，故应先计算出工序尺寸A₃。

根据题意作出工艺尺寸链简图，如图1-19b所示。

由于面A、B、C在镗孔前已加工，故A_l、A₂在本工序前就已被保证精度，A₃为本工序直接保证精度的尺寸，故三者均为组成环，而A₀为本工序加工后才得到的尺寸，故A₀为封闭环。由工艺尺寸链简图（图1-19b）可知，组成环A₂和A₃是增环，A₁是减环。为使计算方便，现将各尺寸都换算成平均尺寸。由此列竖式得

解得