发电运行控制策略优化

交流励磁变速恒频DFIG风力发电系统并网前后发电机的运行状态和控制策略均不相同，并网前空载运行，实施空载并网控制；并网后发电运行，实施最大风能追踪控制。

图6-6为风力机运行过程中功率与转速的关系曲线。其中形状类似抛物线的曲线为不同风速下符合风力机特性的功率-转速关系曲线，从下到上风速依次增加，连接各条曲线峰值点构成的曲线为最大功率曲线（即最大功率追踪控制时的有功功率给定参考曲线），下面参照此图对采用功率给定控制的最大风能追踪过程进行分析。

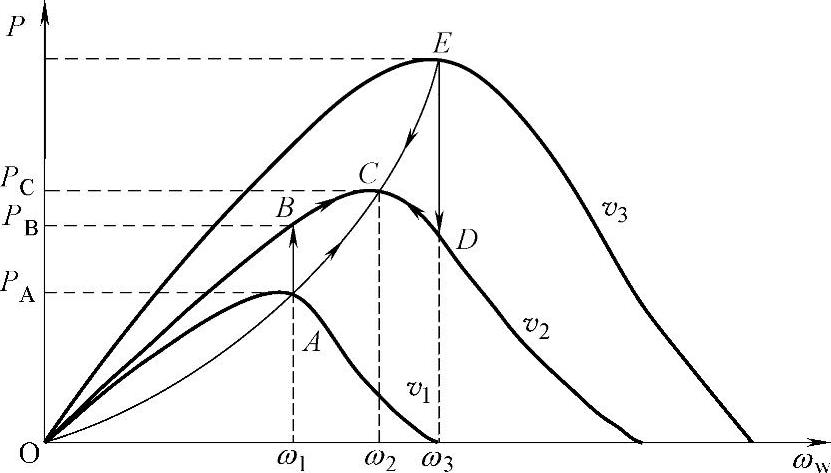
图6-6 最大风能追踪过程分析

假设原来在风速v₁下，风力机稳定运行在P_opt曲线的A点上，此时风力机的输出功率和发电机的输入功率相平衡，都为P_A，风力机稳定运行在转速ω₁上。如果某时刻，风速升高至v₂，风力机的运行点就会由A点跳至B点，输出功率突变至P_B，由于惯性和调节过程的滞后，发电机仍暂时运行在A点，其输入功率大于输出功率，功率失衡导致转速上升。在转速增加的过程中，风力机和发电机分别沿着B-C和A-C曲线增速，当达到风力机功率曲线与最佳曲线相交的C点时，功率再一次平衡，转速稳定为ω₂，ω₂就是对应于风速v₂的最佳转速。同理，风速由v₃下降到v₂也可用类似的方法分析。

最大风能追踪的机理就是通过控制DFIG输出有功功率，控制DFIG的电磁阻转矩来实现最佳转速控制。在实际发电运行中，除了要控制DFIG的输出有功功率以外，还需控制DFIG的输出无功功率，综合称之为DFIG的功率控制。DFIG功率控制的优劣直接影响风力发电系统的最大风能追踪效果、风电并网的电能质量以及发电机的运行特性。

由于交流励磁变速恒频双馈发电机风力发电系统是一个高阶次、非线性、强耦合的多变量系统，若用常规的控制方法将十分复杂，而且效果也难以令人满意，本书采用定子磁链定向矢量控制实现电机功率之间的解耦及最大风能追踪控制。

因为交流励磁电机的定子绕组直接接在大电网的低压侧，可以近似地认为定子的电压幅值、频率都是恒定的，所以交流励磁双馈发电机一般多选择定子电压或定子磁场定向方式。这里采用定子磁链定向，将同步旋转dq坐标系的d轴定向在定子磁链Ψ₁方向上。依据发电机惯例的定子磁链定向矢量空间关系示意图如图6-7所示。

此时，d、q轴上的磁链分量分别是：ψ_ds=ψ₁，ψ_qs=0。由于DFIG定子侧频率为工频，定子绕组电阻远小于定子绕组电抗，可以忽略，即R_s=0，DFIG感应电动势近似等于定子电压，按照发电机惯例，感应电动势e₁滞后磁链ψ₁90°，故e₁位于q轴负方向，有u_ds=0，u_qs=-u₁，其中u₁为定子电压矢量的幅值，当定子端并入理想电网时，u₁等于电网电压矢量，为常数。

因为在交流励磁双馈式风力发电系统矢量控制中，被控制的是转子电压、电流，所以必须从数学模型中找到转子电流分量与其他物理量的关系。

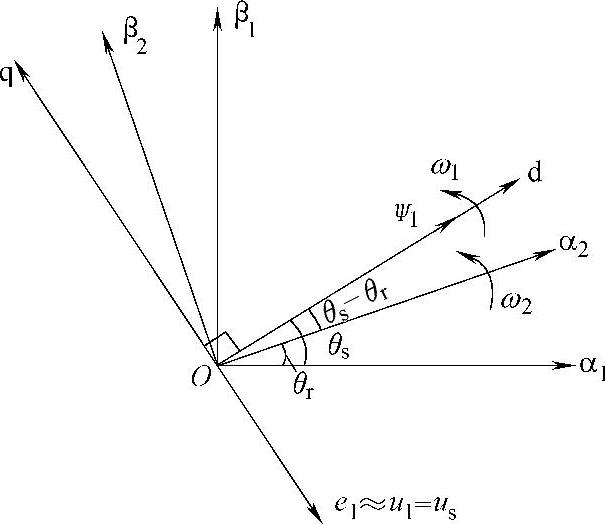
图6-7 定子磁链定向矢量空间关系示意图

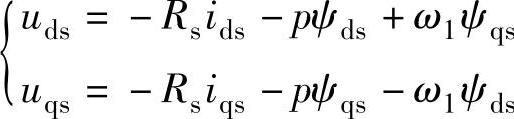将R_s=0，u_ds=0，u_qs=-u₁，ψ_ds=ψ₁，ψ_qs=0代入定子绕组磁链方程和电压方程和可得

由上式可知，双馈发电机并入理想电网后，其定子磁链将保持恒定，幅值为电网电压与同步角速度之比。

将式（6-16）代入转子磁链方程可得

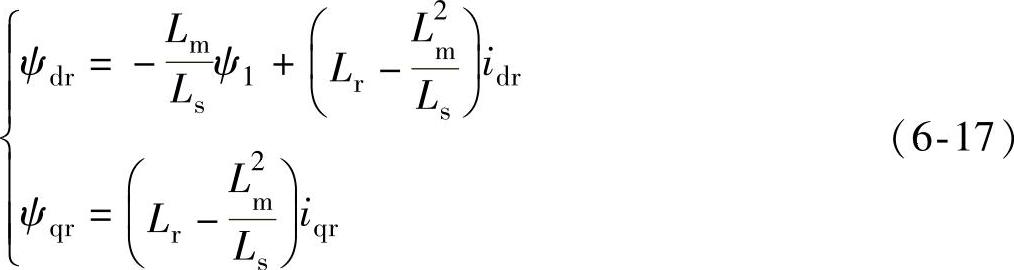
令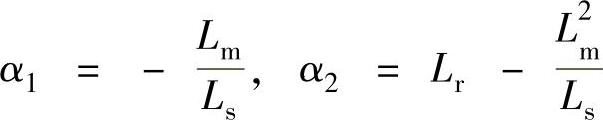，将其代入转子绕组电压方程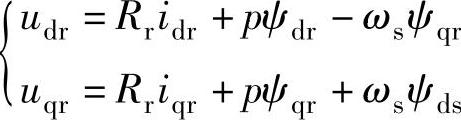得

式中，u_dr′、u_qr′为分别与i_dr、i_qr具有一阶微分关系的电压分量；Δu_dr、Δu_qr为解耦电压补偿分量。(www.xing528.com)

其中

由上式可知，可以分别设计d、q轴的电流PI调节器。

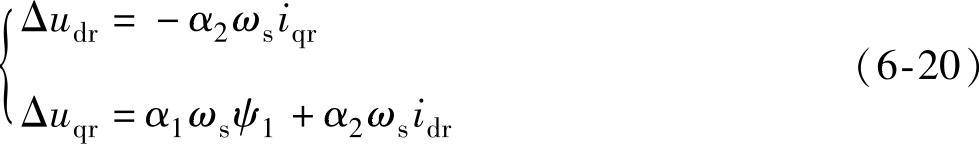
式中，u_dr′、u_qr′为实现转子电压、电流解耦控制的解耦项；Δu_dr、Δu_qr为消除转子电压、电流交叉耦合的补偿项。

将转子电压分解为解耦项和补偿项，既简化了控制，又保证了控制的精度和动态响应速度。在经过前馈补偿去掉由反电动势引起的交叉耦合项后，可以通过调节转子电压的d轴和q轴分量分别控制发电机的转子磁链和电磁转矩。由（6-16）式，得将上式代入电磁转矩方程式得

由上式可以看出，当定子磁链ψ₁保持恒定时，电磁转矩与转矩电流i_qr成正比。根据瞬时功率理论，DFIG在两相同步旋转坐标系下的定子侧瞬时有功、无功功率可写为

在定子磁链定向矢量控制策略下，将u_ds=0，u_qs=-u₁代入上式可得

由上式可知，在定子磁链定向控制下双馈发电机定子输出有功、无功功率分别与定子电流在q、d轴上的分量成正比，故调节i_qs和i_ds可分别独立调节有功和无功功率。

式（6-15）～式（6-24）构成了双馈发电机定子磁链定向矢量控制下的完备数学模型。根据以上讨论，可以得出DFIG风力发电系统定子磁链定向矢量控制策略框图，如图6-8所示。

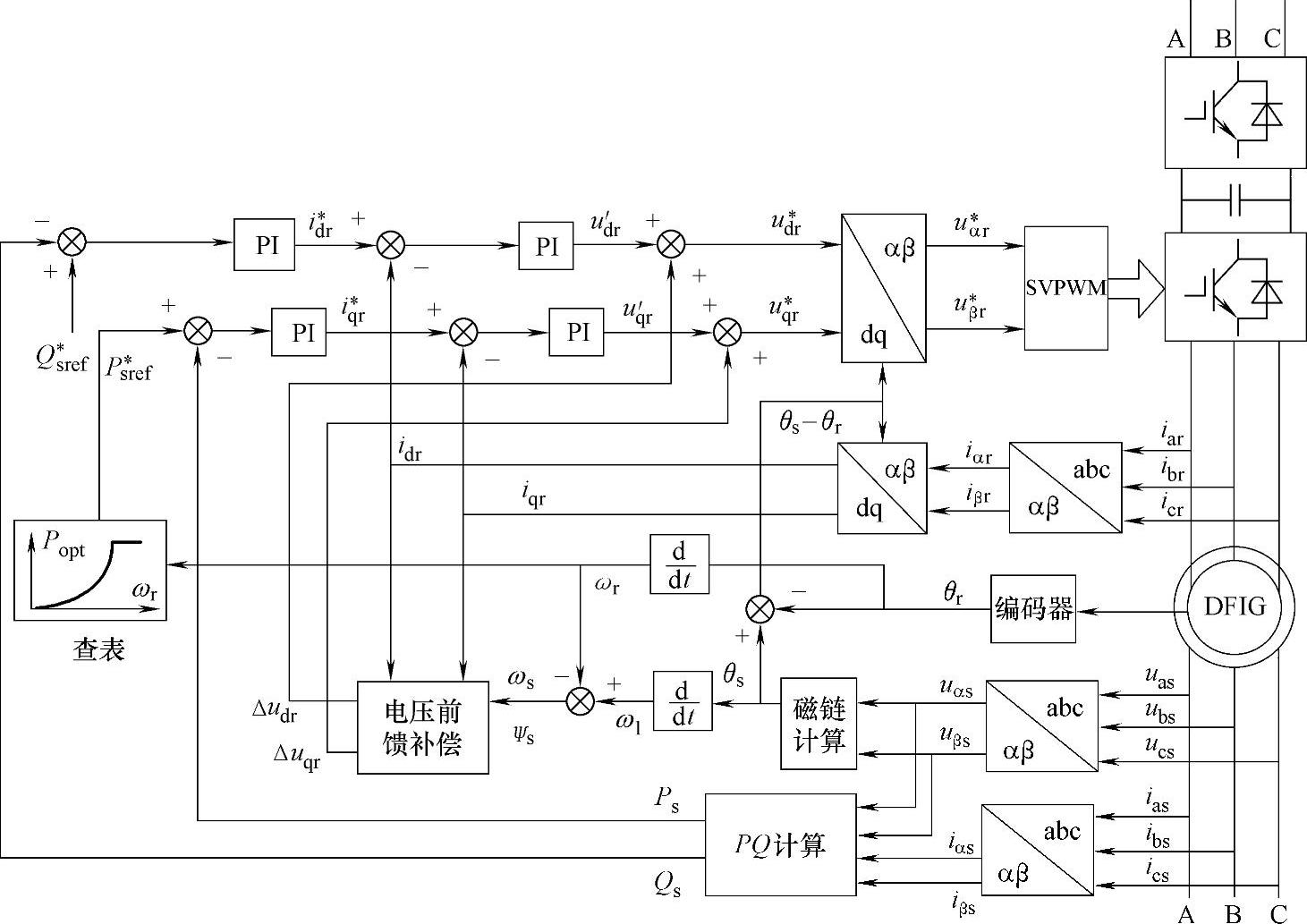
图6-8 变速恒频风力发电系统控制框图

整个系统为双闭环结构，内环为转子电流控制环，由i_dr、i_qr两个控制通道组成，均采用带积分和输出限幅的PI调节器，电流误差经调节后输出电压控制量，叠加Δu_dr、Δu_qr前馈电压补偿量，即可得到同步旋转坐标系中的转子电压控制量，再经坐标变换得到双馈发电机转子两相静止电压控制指令u_αr^*、u_βr^*，经SVPWM调制后产生所需的励磁电压及电流。外环为功率控制环，根据有功、无功功率给定和经过计算得出的反馈值进行比较后输入PI控制器，有功功率控制环节可等效简化为转速控制环，根据当前的风速计算出对应于风力机最佳叶尖速度比的转速值作为转速环的给定，和电机转速反馈值比较后的差值送入带积分和输出限幅的PI型控制器。另外，如果从减少转子励磁电源双PWM变换器损耗的角度考虑，则最好将无功功率设定为0。

磁链计算—定子磁链观测器单元采用一种实用和简单的u-ω型磁链观测器，其变量运算关系如图6-9所示。由于DFIG定子磁链矢量Ψ₁超前于定子电压矢量u₁90°，若u₁相角为θ_u，则Ψ₁的相角θ_s为θ_s=θ_u+90°；Ψ₁可由ψ₁=u₁/ω₁得出。

图6-9 u-ω型定子磁链观测器