深入解析空间电压矢量脉宽调制

空间电压矢量脉宽调制（Space Vector Pulse Width Modulation，SVPWM）技术与常规的正弦波脉宽调制（SPWM）相比具有直流母线电压利用率高，电流波形畸变小和易于数字化实现等优点，因而在电力电子与电气传动领域获得越来越广泛的应用。采用SVPWM技术即使不做过调制处理，变换器输出交流线电压基波的最大值为直流母线电压，也比采用一般的SPWM的变换器的输出交流电压高了15%。

MATLAB/Simulink是当前最为流行的仿真软件之一，其中的SimPowerSys-tems库包含电气传动领域中的大部分模块，大大方便了仿真研究。但是没有现成的SVPWM模块，因此在对变速恒频双馈风力发电机转子交流励磁用双PWM变换器的仿真中，需要自行构造SVPWM的仿真模型。本书下节内容对此作详细介绍。

空间电压矢量控制在电机传动系统已得到广泛的应用，本文将空间电压矢量控制技术引入到双馈发电机双PWM变换器，典型的网侧变换器结构可参照图1-6。

图中6个开关器件选用IGBT，对其进行编号，上桥臂从左到右为1、3、5，下桥臂对应为4、6、2。1、3、5号IGBT的开关状态将决定变换器的输出，假设线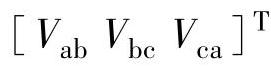电压为、相电压为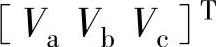、开关变量为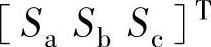、直流侧供电电压为V_dc，应用坐标变换理论，推导过程如下：

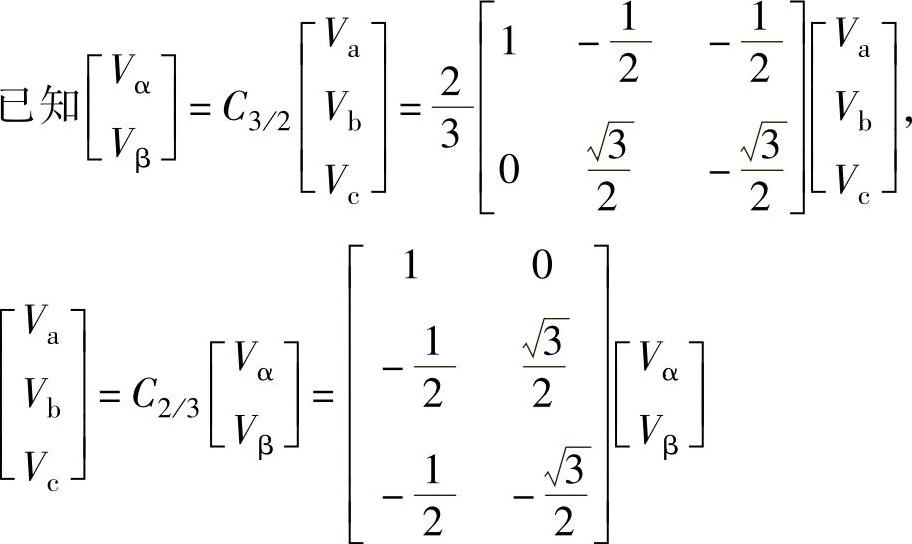
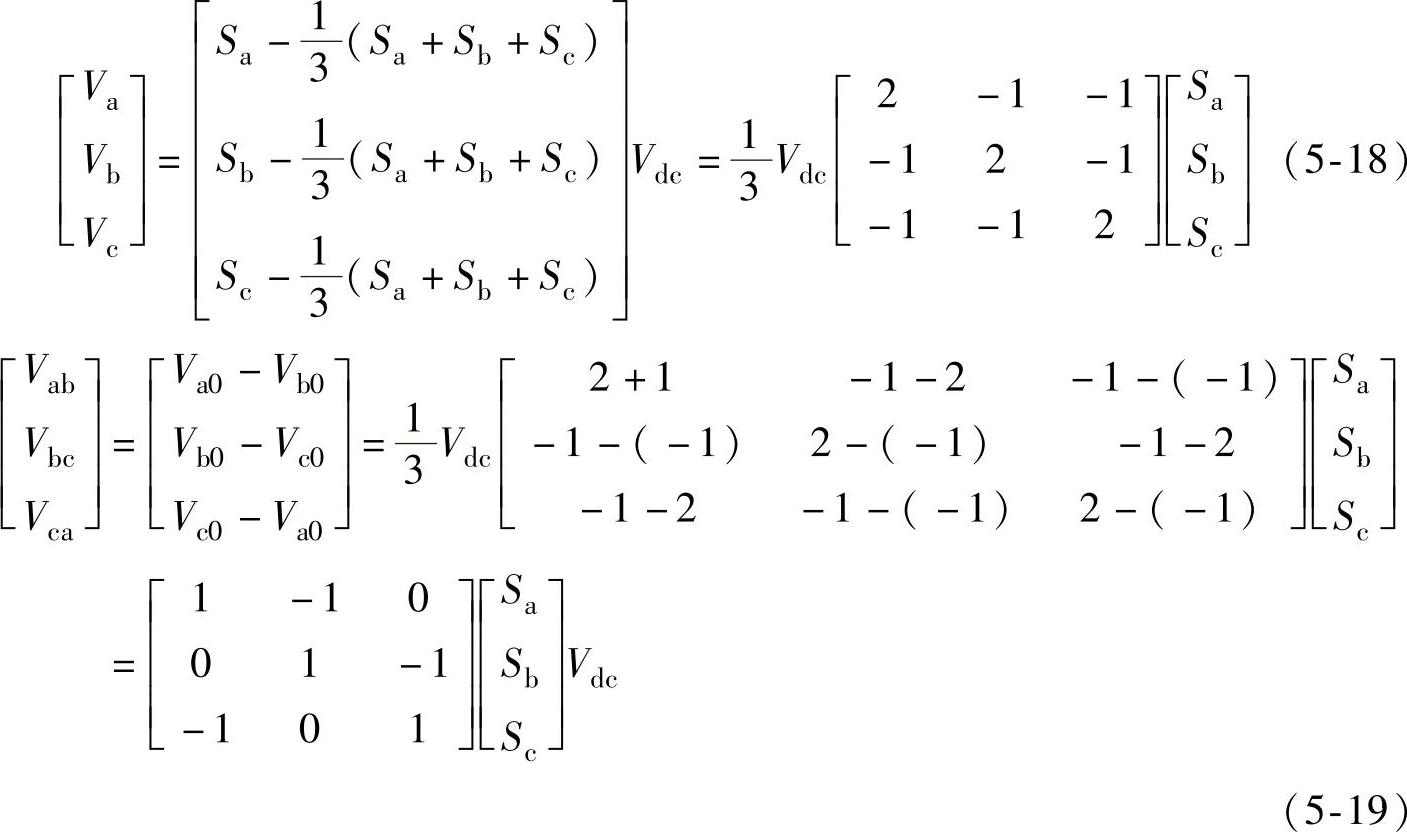
可以看出，逆变器工作时，有八种可能的开关组合。根据式（5-18）和式（5-19），若以V_dc为基准值，则逆变器的输出线电压和相电压见表5-1。

表5-1 功率管开关状态及相应逆变器的电压关系

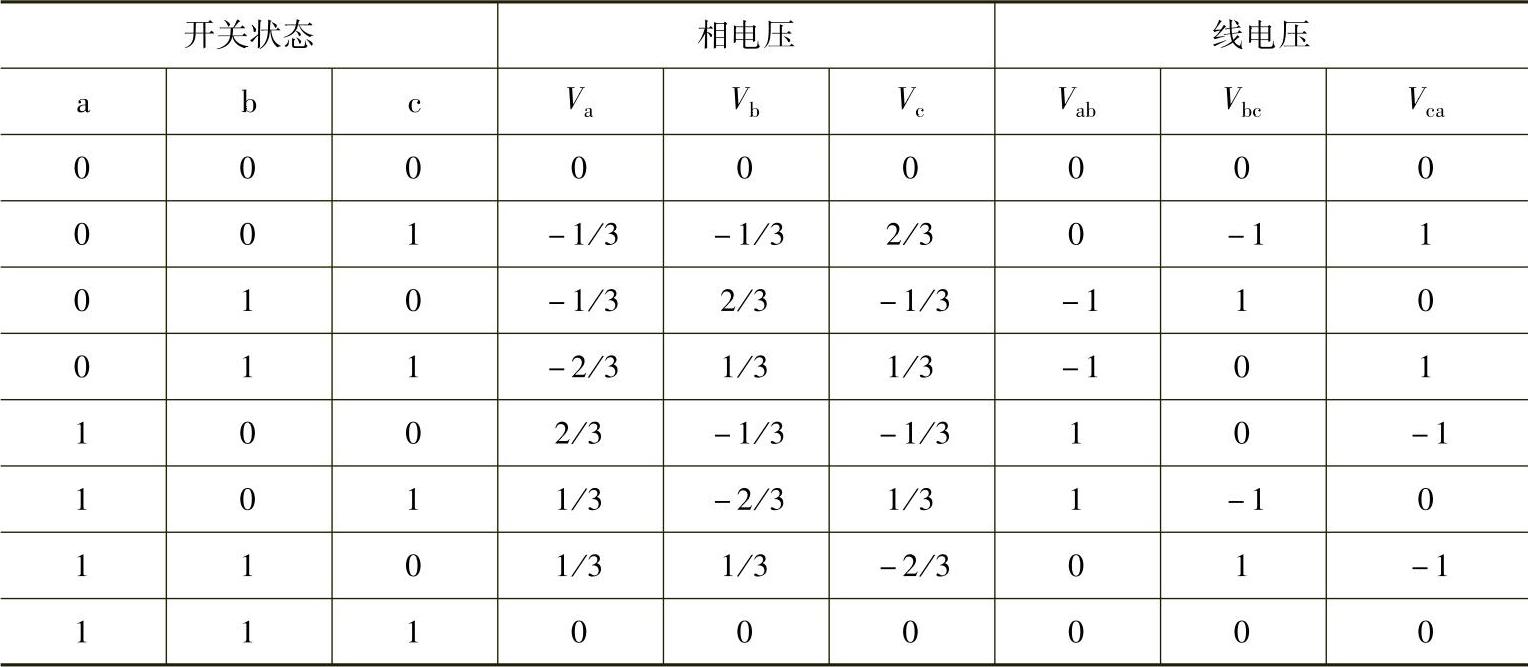
在dq坐标系中，输出的三相相电压相对应的d、q分量可以用下式表示：

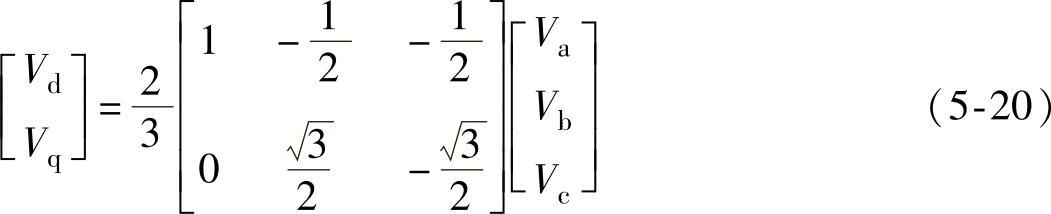
上式把八种开关状态组合映射到dq坐标系，并相应得到六个相互间夹角为60°的非零电压向量和两个位于坐标原点的零电压向量，这八个向量称作基本空间矢量，并将空间分成了六个扇区，如图5-8所示。

SVPWM控制的目的是通过与基本的空间矢量对应的组合得到一个给定的参考电压矢量U_out。由于逆变器能够产生的基本电压矢量只有八个，因此在已知参考电压矢量后可以根据伏秒特性相等的原理来使输出电压矢量逼近参考电压矢量。若知道参考电压矢量位于哪一个60°扇区，就可以选择与其相邻的两个基本空间电压矢量及零矢量并控制它们的作用时间来等效参考电压矢量。

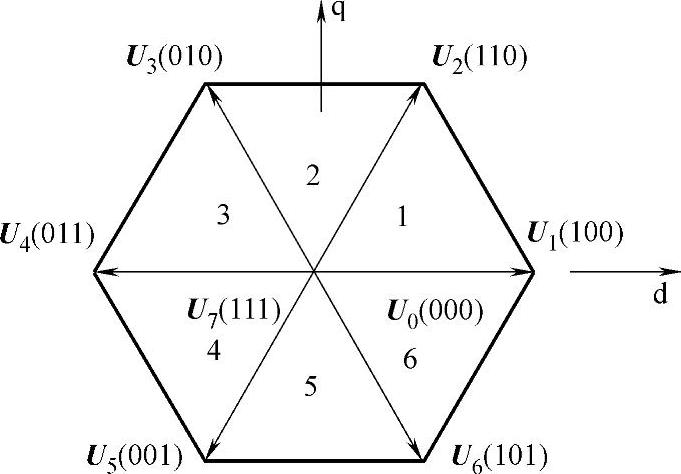
图5-8 基本电压空间矢量图

本书对其算法作如下说明，假设参考电压矢量U_out位于1扇区，则U_out可以用U_0°和U_60°两个矢量来表示。于是有如下等式：

用dq坐标系描述，则有：

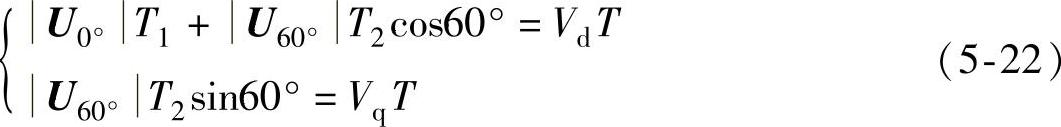(www.xing528.com)

式中，T为开关周期；T₁、T₂为U_0°、U_60°作用时间；T₀为零矢量作用时间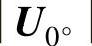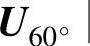；、的幅值都为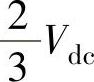，可计算得到

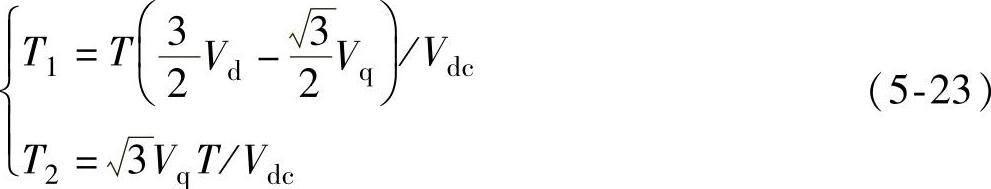
同理，可计算参考矢量在其他扇区时相邻矢量的作用时间。当然，必须进行饱和判断，即如果T₁+T₂＞T，则取：

由前面分析可知，如果要计算T₁、T₂，则必须要知道参考电压矢量所在的扇区。设N=A+2B+4C，如果定义：

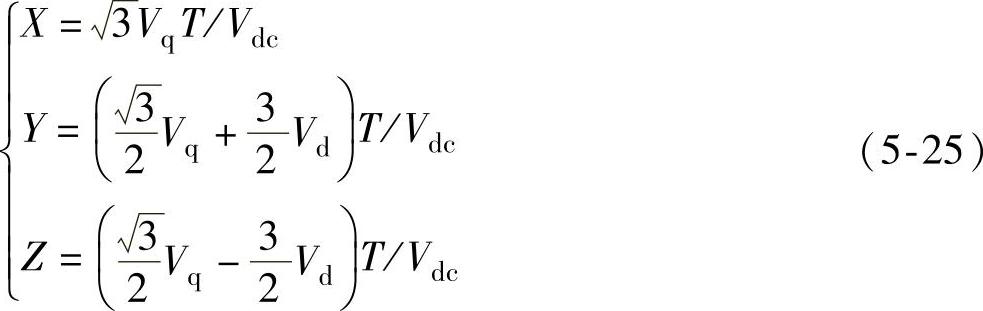
有一种简便判断扇区的方法：若V_q＞0，则A=1，否则A=0；若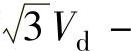V_q＞0，则B=1，否则B=0；若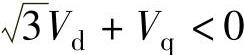，则C=1，否则C=0。通过以上分析可得N与扇区及矢量作用时间T₁、T₂的关系，见表5-2。

表5-2 N与扇区及矢量作用时间T₁、T₂关系表

若已知SVPWM的调制周期T，根据上面的算法很容易计算相邻矢量作用时间。但必须合理选择零矢量000和零矢量111，才能限制开关频率，减少开关损耗。选择零矢量的原则是，使逆变器开关状态每个周期只变化一次。确定好每个扇区开关状态的先后顺序，以减少不必要的开关动作。以扇区1为例，如图5-9所示。假设零矢量000和111在一个开关周期中作用时间相同，生成的是对称PWM波形，可把每个基本空间矢量作用时间都一分为二，按000、100、110、111、110、100、000的作用顺序，可以看出，每次只有一个开关变化。

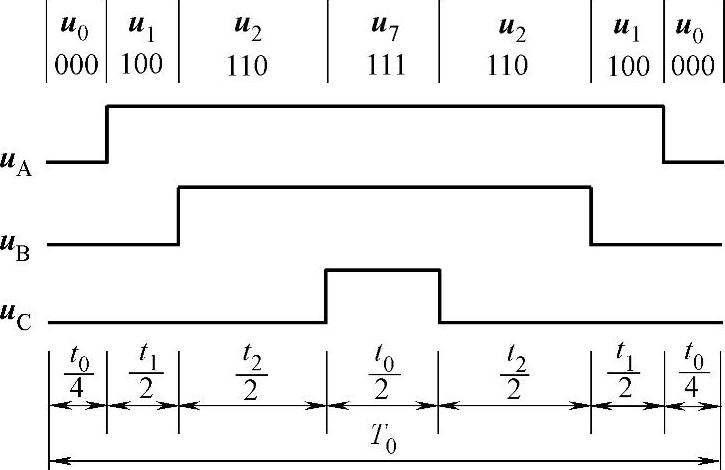
图5-9 扇区1的工作波形

定义开关切换点距离零点时间为T_u、T_v、T_w，可得到

T₁对应最先作用的矢量时间，T₂对应另外一个非零矢量作用时间。那么T_u、T_v、T_w在一个开关周期中具体分给哪个比较值，由各扇区的波形确定。T_u要分给占空比最大的相，T_w分给最小的相。通过各个扇区的工作波形，就可得出相关的切换点，见表5-3。

表5-3 切换点赋值表