直接功率控制的原理解析

根据双馈发电机的基本原理，可得双馈发电机在固定转速ω_r下，在转子定向坐标系α_r、β_r下的等效电路如图4-15所示。

定子磁链和转子磁链在静止和旋转坐标系下的矢量图如图4-16所示，在以转子转速ω_r为参考的两相同步旋转坐标系下，定子和转子磁链的表达式为

式中，ψ_s、ψ_r为定、转子磁链；I_s、I_r为定、转子电流；V_s、V_r为定、转子电压；L_m、L_σs、L_σr为互感、定、转子漏感；L_s、L_r为定、转子绕组自感；R_s、R_r为定、转子绕组电阻；s上标表示静止坐标系；r上标表示旋转坐标系；s下标表示定子；r下标表示转子。

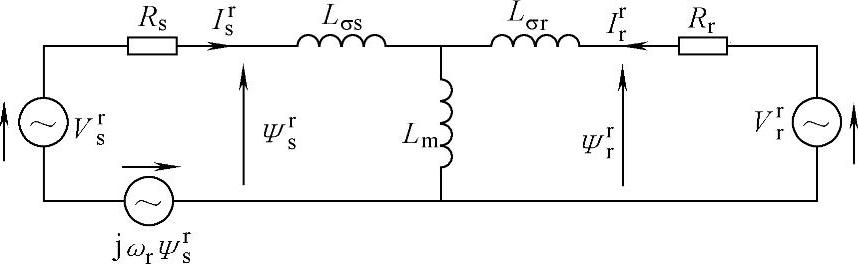
图4-15 双馈发电机在旋转坐标系下的等效电路图

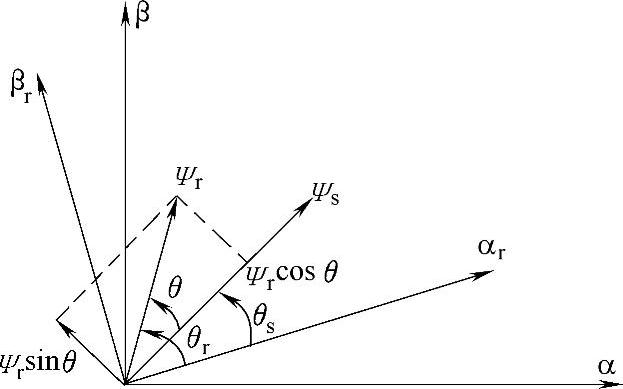
图4-16 定子磁链和转子磁链在静止和旋转坐标系下的矢量图

根据上式可以得到定子电流的表达式：

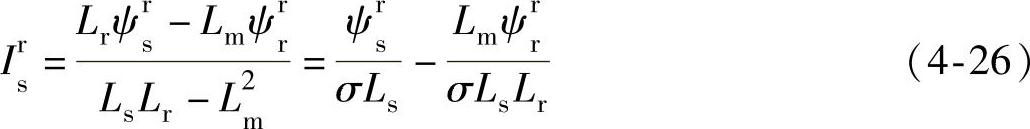
式中，σ为漏磁系数，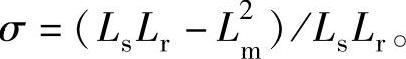

参考图4-15，定子电压矢量表达式为

定子侧输入的有功功率可以表达为

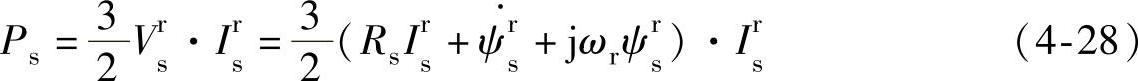
忽略定子铜耗，上式可简化为

同理，定子侧输入的无功功率可表达为

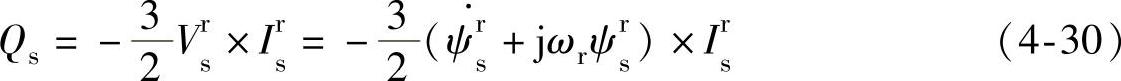
图4-16显示了定子磁链和转子磁链在αβ静止坐标系下和α_rβ_r旋转坐标系下的关系。定子磁链和转子磁链在α_rβ_r旋转坐标系下的表达式为

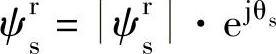
定子磁链在两种坐标系下的关系为(www.xing528.com)

由图4-16可知：

θ_s=ω₁-ω_r （4-33）

在静止坐标系中，定子磁链可表示为

由于风机具有比较大的惯性，假设与定子相连的电网是稳定的，并且转子转速在采样周期内不变，忽略定子电阻，由式（4-32）可得

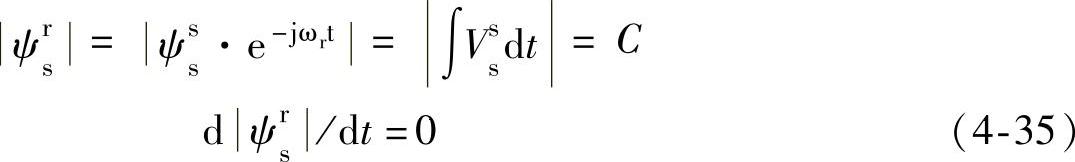
对式（4-31）第一式求导，同时把式（4-32）、式（4-33）代入可得

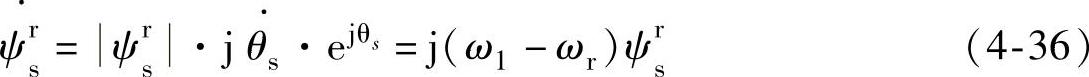
把式（4-25）和式（4-26）代入式（4-29）和式（4-30）可得定子侧的有功功率输入和无功功率输出的表达式为

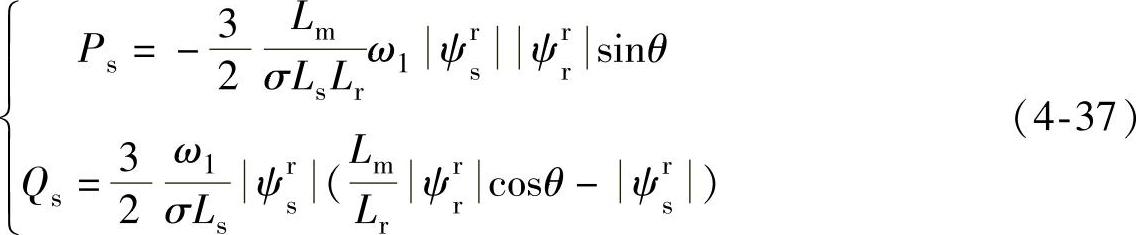
式中，θ为转子磁链和定子磁链矢量的夹角，θ=θ_r-θ_s；各个矢量的关系参照图4-16。

对式（4-37）求导可得

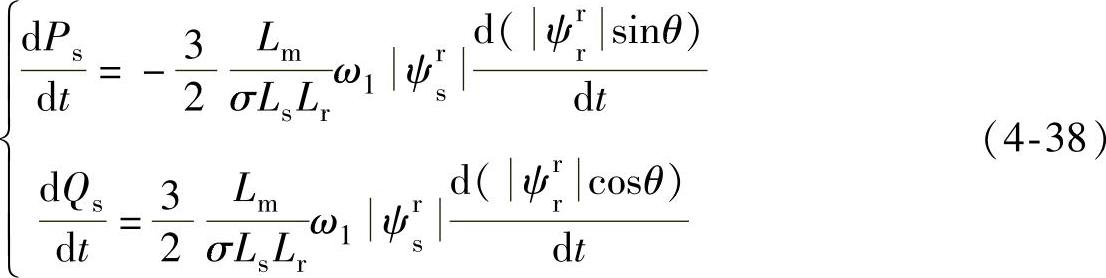
从上式可以看到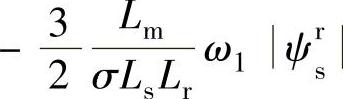为恒定的参数，变量为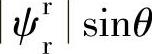和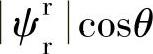，所以通过分别调节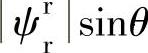和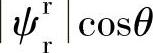就可以达到分别控制有功功率和无功功率的目的，这说明定子有功功率和无功功率的控制可以转化到对转子磁链的控制。

图4-17为两电平变换器和开关电压矢量图。由图4-17a可知，三相桥的每一个桥臂输出的相电压v_a、v_b和v_c都有两个值，分别为0和+V_d，这样开关电压矢量V_n（abc）共有八种组合，分别为：V₀（000）、V₁（001）、V₂（010）、V₃（011）、V₄（100）、V₅（101）、V₆（110）和V₇（111），其中“0”表示上桥臂关断下桥臂开通，“1”表示上桥臂开通下桥臂关断，且V₀（000）和V₇（111）是零矢量，其余为非零矢量。

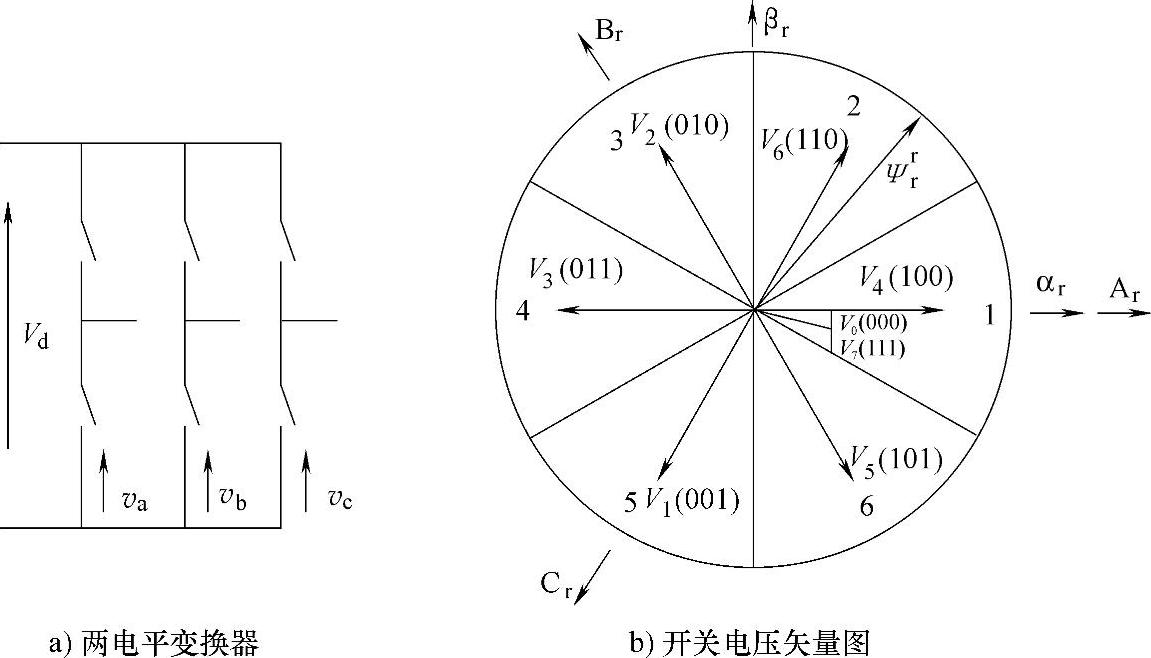
图4-17 两电平变换器和开关电压矢量图

忽略转子电阻，转子磁链的微分在旋转坐标系下表达为

由上式可见转子磁链的变化可以归为转子电压的变化：转子磁链按照转子电压矢量的方向移动，速度和电压矢量的幅值成比例。因此通过选择适当的开关矢量就可以控制转子磁链的运动方向，如图4-17b所示，电压矢量的选取与转子磁链所属扇区有关。