悬移质对水流能量的影响

（一）能量损失在空间分布的变化

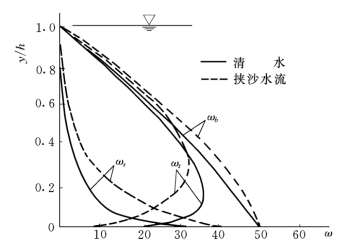
图7-30　清水及挟沙水流各能量指标沿水深的分布（钱宁，万兆惠，1983）

在二维明渠的主流区，单位水体单位时间所提供的能量Wb、就地损失的能量Ws，及水体向边界传递的能量Wt之间满足能量平衡关系。挟沙水流中悬浮泥沙改变紊动特性和时均流速分布的结果，将使能量损失在空间上的分布也发生变化。图7-30为钱宁和万兆惠根据水槽清浑水试验资料计算的上述三种能量指标自水面至某一高程累积值沿水深分布的对比。由图可见：①在水流上部的主流区，和清水相比挟沙水流能够提供更多的能量，在水流下部，则情况正好相反；②在绝大部分流区内，由于挟沙水流的流速梯度较大，因而就地消耗的能量也比清水水流为大，在十分贴近床面的流层内，清水水流比挟沙水流有更为集中的能量消耗；③与能量的提供和消耗相对应，挟沙水流中能量自主流区向近底流层的传递不复象清水水流那样集中。

（二）悬移质运动影响能量损失的分析

有了悬移质泥沙运动后，水流的势能转化为热能的全过程将发生相应的变化。这个变化比较复杂，目前对许多细节还不清楚，因而也就缺乏一个统一的理论可以对各种阻力损失现象作出解释。但从定性上，可以对悬移质影响水流能量损失的作用作如下分析：

（1）从固体颗粒置换流体所带来的流场变化考虑。与清水水流相比，挟沙水流中有一部分流场的空间为固体颗粒所占据，减少了通过粘性转化为热能的流体的有效空间（或体积）。从这一角度考虑，固体颗粒的存在使能量损失减少。

（2）从挟沙水流的粘性不同于清水考虑。泥沙颗粒的存在使挟沙水流的粘性增加，从而使近壁区粘性底层的厚度增大。如果水流周界原来是水力粗糙区或处于过渡区，则粘性底层厚度的增大将使周界变得相对光滑，从而使水流能量损失减少。细颗粒泥沙对挟沙水流粘性增大的作用更为显著，因而对阻力的影响也较大。如果周界原来就是水力光滑的，则挟沙水流粘性和粘性底层的变化将对阻力没有影响。

（3）阻力系数和雷诺数的关系因流态及边界条件不同而划分为三个区域，在不同的区域内，阻力系数与雷诺数的关系不同。若在相同的流速和水深下进行比较，由于挟沙水流的粘性要比清水大得多，因此其雷诺数要比清水水流小得多。在层流区及光滑紊流区，特别是在层流区，挟沙水流的阻力系数就有可能大于清水水流。

（三）悬移质运动影响能量损失的有关试验研究成果

对于悬移质泥沙对水流能量损失影响这一问题，现有的试验成果显示出很大的分歧。下面分别介绍有关的试验研究成果。

1.悬移质运动使水流能量损失减少的试验结果

（1）黄河、长江的实测资料。张瑞瑾（1989）收集了黄河的实测资料，点绘曼宁粗糙系数n与含沙量的关系，发现n值随含沙量增大而减小（见图7-31），说明悬移质使阻力减小。和试验水槽研究相比，天然河道的情况要复杂得多，影响阻力系数或糙率系数的因素众多，变化幅度常常很大，因此图中点子的分散度较大是可以理解的。但n随含沙量的增加而减小的客观事实是确实存在的。长江中下游的实测资料也有同样的规律。

（2）水槽试验资料。Vanoni&Nomicos（1960）在保持周界相同的前提下，在水槽中量测对比清水和不同含沙量条件下阻力损失的变化，发现沙波的发展消长对阻力损失起重要作用。在同样的边界条件下，悬移质存在使阻力系数减少4%～20%。张瑞瑾（1989）在水槽试验中，得到在不同的含沙量下阻力系数变化规律：随含沙量的增加，阻力系数有明显的降低趋势。

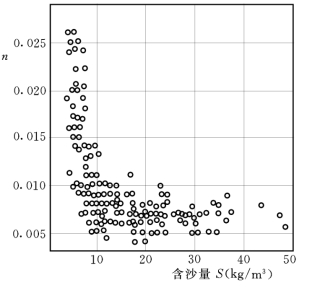
图7-31　黄河下游糙率系数随断面含沙量的变化（张瑞瑾，1989）

Wang et al.（1998）对较高浓度的含沙水流在光滑、粗糙床面下阻力特性进行了试验研究。结果表明，在粗糙床面下，含沙水流的能量损失较清水显著降低。

2.悬移质运动使水流能量损失基本不变的试验结果

Einstein&Chien（1955）保持周界相同的前提下，在水槽中量测对比清水和不同含沙量条件下阻力损失的变化，在相近的试验条件下，挟沙水流的能量损失与清水没有明显的不同。Wang&Qian（1989）的试验也得到了同样的结论。

3.悬移质运动使水流能量损失增加的试验结果

MIT的学者用轻质颗粒的试验研究表明，随着含沙量的增大，阻力系数增大（Elata&Ippen 1961；Daily&Hardison 1964；Daily&Roberts 1964）。Montes&Ippen（1973）用石英沙（D50=0.365mm）和天然沙（D50=0.132mm）以及其混合物在光滑槽壁、较陡底坡条件所作的试验，发现同样的规律，即挟沙水流的阻力系数显著大于清水，含沙量愈大，阻力系数也愈大，如图7-32所示。(www.xing528.com)

图7-32　阻力系数与含沙量的关系（Montes&Ippen 1973）

Bruhl&Kazanskji（1976）管道试验表明，中径0.3mm的粗颗粒悬浮输移时，水头损失显著大于清水。加入0.01mm以下的细颗粒时，水头损失比只有粗颗粒时有所减少。

万兆惠等在宽0.4m、高0.4m、长24m的活动循环水槽中进行高含沙水流试验，槽壁及槽底均由玻璃组成。D50=0.042，0.056mm，含沙量最高达到900kg/m3。以相同的雷诺数作为比较的前提，则挟沙水流的阻力系数略小于清水的相应值。若以相同的水深和流速作为比较的前提，高含沙水流的阻力系数显著大于清水的相应值。

Lyn（1991）研究了在平衡输沙和非平衡输沙条件下挟沙水流的阻力特征，在分析试验资料时强调必须把阻力系数的变化和流速分布的变化结合起来考虑。试验所用泥沙颗粒直径为：0.15mm，0.19mm，0.24mm，流速分布用激光流速仪量测。试验结果表明，悬沙的加入使阻力系数增大。图7-33为悬沙水流和清水阻力系数的比较。他同时分析了Coleman（1981）及Parker&Coleman（1986）的资料，点绘了悬沙水流与清水阻力系数比和Richardson数的关系，结果如图7-34所示。图7-33和图7-34清楚地表明了含沙水流阻力系数明显大于清水水流的阻力系数。

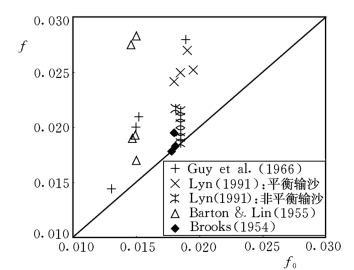
图7-33　悬沙水流和清水阻力系数的比较（Lyn 1991）

4.悬移质运动使水流能量损失有各种不同变化的试验结果

Mih（1972）根据有关的试验资料，认为挟沙水流的能量损失大于、等于或小于清水水流的能量损失的可能性都是存在的。他从对数流速分布公式出发，得到光滑圆管的阻力系数为：

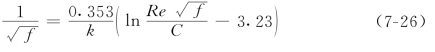
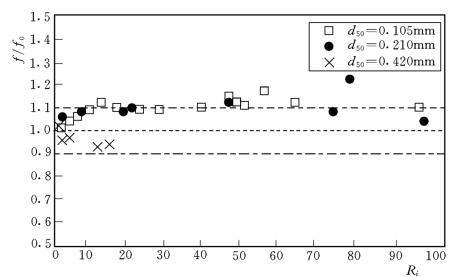
图7-34　悬沙水流和清水阻力系数的比和Richardson数的关系（Lyn 1991）

式中：Re=Ud/ν，d为管径。有关资料（Daily&Hardison 1964；Daily&Roberts 1964）表明，k与C是体积比颗粒浓度的函数，k随浓度的增大而减小，而C随浓度的增大而增大，即上式中的系数k与C随着含沙量的增大而有不同的发展趋势，这样，根据这两种发展的对比消长，挟沙水流的阻力损失比较起来，就可能出现各种不同的情况。

Arora et al.（1986）的定床挟沙水流试验也表明，挟沙水流的阻力系数和清水水流相比也存在不同的情况。试验的大致情况为：颗粒粒径d=0.082～0.164mm，比重2.04～2.65，体积比浓度34～6562ppm，水流Re=7×104～3×105，Fr=0.60～1.30。挟沙水流和清水阻力系数的比较如图7-35，其中横坐标为克服浓度梯度做功与克服阻力做功的比值。显而易见，当大于1200时，挟沙水流阻力损失大于清水水流的能量损失，但小于1200时，情况恰恰相反，挟沙水流的能量损失比清水水流要小。这表明，若悬浮泥沙为细颗粒或浓度很小，挟沙水流的阻力损失较清水小；若颗粒粒径较大或浓度较大，阻力损失增加。Arora et al（1986）认为，细颗粒泥沙存在会使紊动减弱，阻力损失减小；若颗粒粒径较大或含沙量较大，悬浮泥沙会造成额外的能量损失，从而使能量损失增大。他认为能量损失应该和参数有密切的关系。根据其试验资料，点绘了f/f0和的变化趋势，见图7-36，可见f/f0随的增大而增大。

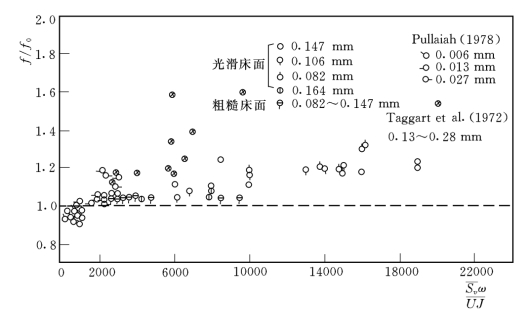
图7-35　阻力系数与参数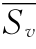ω/UJ的关系

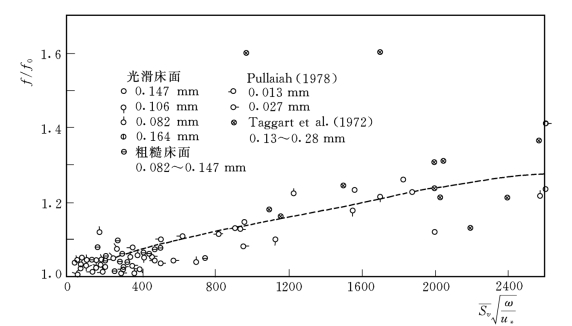
图7-36　阻力系数与参数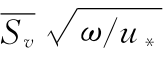的关系

需要指出的是，研究悬移质运动对水流能量损失的影响时，必须排除周界条件变化这一因素，而且试验研究时要严格控制泥沙全部处于悬浮状态，以避免推移质运动产生的影响。其次是比较的标准问题：是用同一雷诺数作为标准还是用同一流速（及水深）作为标准，所得的结论不一定相同。另外需要说明的是，紊动减弱并不等同于能量损失减少。因为紊动能取自水流的有效势能，并最终转化为热能。悬移质的存在需要紊动动能来支持，但是紊动动能本来就是能量转化过程中的中间媒介物，取出部分紊动动能支持泥沙悬浮并不意味着有效势能转化为紊动动能的数量减少，所以说紊动减弱并不等同于能量损失的减少。

还应指出，冲积河流阻力的影响因素中，一般来说，含沙量与床面形态相比是次要因素，悬沙耗能仅占有效能量的百分之几，但对高含沙水流而言，情况有所不同，可参考钱宁编写的《高含沙水流运动》。