挟沙水流的能谱密度分析

能谱密度分布给出了总的紊动能量沿频率的分布，在工程上可以把紊动能量最大的频带作为设计依据。明渠清水水流能谱密度分布特征已经有了比较深入的认识，参见Nezu&Nakagawa（1993）。悬移质运动的存在，使水流的能谱密度分布产生很大的变化。

泥沙的悬浮是泥沙被向上运动的水团所举起，同时它又相对于周围水体下沉的综合结果。只有比泥沙粒径大得相当多的水团方能有效地将泥沙举起，即泥沙的上升需要从尺度比它大得多的漩涡中取得紊动动能。另一方面，泥沙在下沉的过程中，颗粒与周围水体有垂直方向的相对运动，一部分释出的位能将因摩擦而散失为热能，另一部分位能将转化为泥沙颗粒尾迹中所不断产生的涡漩的动能，而这些涡漩的尺寸和泥沙颗粒的大小是同一数量级的。也就是说，在沙粒一升一降的过程中，一方面消耗了部分紊动动能，另一方面使大尺度涡漩的部分能量向小尺度的涡漩转移，带来了紊动频谱的变化。同时，悬沙的存在使水流的粘性增大，这将影响涡漩之间的能量传递过程。挟沙水流中不可能存在象清水水流中那样小的漩涡。由于细颗粒泥沙使水流粘性增大的作用显著，所以也正是细颗粒泥沙使小尺度涡漩消失的作用更加明显。最小尺度涡漩消失，使大尺度涡漩的能量相对增加。

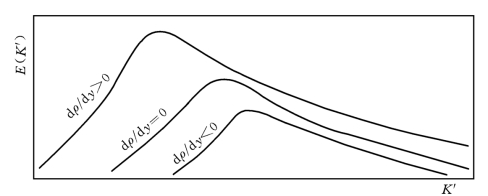
图7-20　紊动能谱的变化（密度梯度对能谱的影响）

Monin（1959）得到了图7-20所示结果。图中横坐标为每单位长度的波数K′，可以看成是涡漩尺度的倒数；纵坐标为是尺度相当于K′的这种涡漩所包含的紊动动能。由图可见，与清水相比（dρ/dy=0），挟沙水流（dρ/dy＜0）曲线的峰型向右方偏移，即有一部分能量由尺度较大的漩涡（K′值较小）转移到尺度较小的漩涡（K′值较大）；与此同时，曲线下总的面积减小，亦即紊动动能总的有所减少。

王兴奎和钱宁（1989）通过试验得到了能谱密度随含沙浓度的变化如图7-21，试验用沙为轻质塑料沙。随着含沙量的增加，紊动的频率降低，大约以10Hz为界，低频分量随含沙浓度而增加，高频分量则随含沙浓度的增加而减小。图7-22为能谱密度分布的底部平均统计参数n50和n90（分别代表50%和90%的紊动能量小于该频率）随含沙浓度的变化特点，图中表明，特征频率随含沙浓度的增加而减小，当体积比浓度达到15%时，n90减小为清水的一半，n50减小得更多，说明紊动能量主要往低频集中。

Lyn（1992）、Hishida et al（1995）的试验资料也证实了悬沙的存在使低频分量增强，而使高频分量减弱。Cellino&Graf（1999）给出了在三个不同水深处能谱密度的试验结果，见图7-23，可见随着泥沙的加入，能谱密度向低频分量偏移。(www.xing528.com)

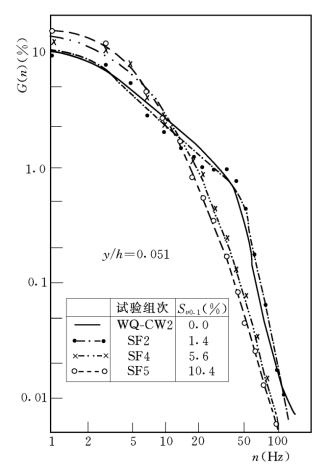
图7-21　紊动能谱分布随含沙浓度的变化（引自Wang&Qian 1989）

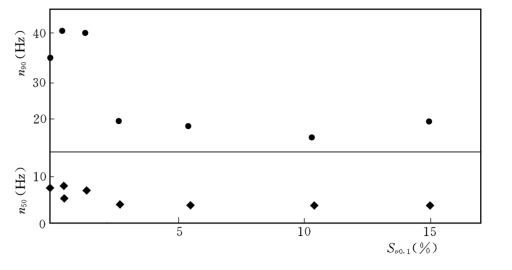
图7-22　紊动能谱分布特征频率随含沙浓度的变化（引自Wang&Qian 1989）

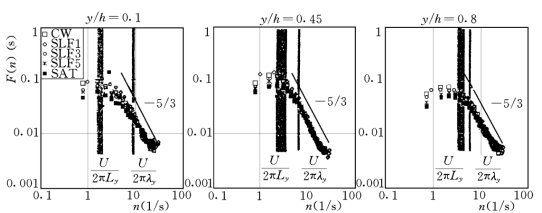
图7-23　能谱密度随含沙量的变化（Cellino&Graf 1999）