混凝土配合比设计中的泥沙扩散理论

（一）扩散方程的解

当悬移质含沙量的垂线分布达到平衡状态时，泥沙扩散问题成为一个均匀、恒定的问题，式（6-11）中对距离x和对时间t的偏微分均等于零。则二维扩散方程为

对y的微分。为了求解式（6-14），首先必须知道εy沿垂线的分布，如假定εy为常数，则式（6-14）的解为

式中：Sva为悬移质泥沙在距床面为a处的体积比含沙浓度。

为了检验式（6-15）是否合理，前人用各种试验方法作了验证，如Rouse（1938）在圆筒中加一组等间距的格栅，使格栅在圆筒中作上下简谐振动，从而在较长一段距离内得到均匀的紊动流场。试验时，在筒中加了四种不同粒径D的泥沙（D=0.0313mm，0.0625mm，0.125mm，0.25mm）。对每一种粒径，量测不同的浓度在各种振动频率下的垂线含沙量分布。试验结果表明含沙量分布基本符合式（6-15）的理论曲线。则根据实测资料，由式（6-15）可以求出εy值。Rouse假定

式中：L为掺混长度，这里即为格栅的振幅；v′为紊动强度，它随格栅的振动频率而变。对某一特定的条件，L和v′均为常数，从实测资料可知，两种细沙（D=0.0313，0.0625）的εy为常数，亦即β为常数。而对较粗的两种沙，εy（亦即β）则有所变化，Rouse认为这是由于颗粒的惯性影响所致。

Rouse试验表明，对某些特定的条件，可以取εy为常数。对于天然河道，可以近似取

进一步的研究表明，泥沙的扩散系数εy不是常数而是空间位置的函数，但现有的理论还不能给出εy沿垂线的分布规律。最常用的方法是假定泥沙扩散系数与动量交换系数εm相等，即假定

将式（6-18）代入式（6-14）得

悬移质垂线分布公式（6-22）中的指数Z确定了泥沙在垂线上分布的均匀程度，Z值越小，悬移质分布越均匀。此外，泥沙的悬浮高度也是Z的函数，根据爱因斯坦的观点，可取Z=5时作为泥沙是否进入悬浮状态的临界判别值。

在式（6-22）的推导过程中，假定扩散系数与动量交换系数相等，即可用式（6-18）表示。如采用不同的表达式，将得出不同的悬沙浓度分布公式。倪晋仁和王光谦（Ni，1991）从式（6-14）出发，假定泥沙扩散系数为

式中：L1为颗粒沿垂线方向运动的特征长度；v为垂向脉动流速，假定为正态分布，进一步假定当v＜0时，的概率密度为零，则

式中：v′为垂向脉动流速的紊动强度。

式（6-23）中的沉速ω与单颗粒静水沉速的关系可表示为

将式（6-24）～式（6-26）代入式（6-14）可得

如取m=1，积分式（6-27）即可得出悬沙浓度分布公式

选取不同的n值，可以得出不同的浓度分布公式。如取n=0，可得出Laursen公式，取n=1，则得出Rouse公式。

刘大有（1985，1993）根据力平衡原理，参照湍流混合气体运动中组元间作用力的本构关系给出了湍流二相流间阻力的本构式，推导出了充分发展的明渠流动中的泥沙浓度垂向分布。当引入某些近似的假定后，可得泥沙运动的扩散方程。

（二）扩散方程的验证

自从20世纪30年代推导出悬移质浓度分布的基本公式后，人们做了大量的工作以验证这一理论公式的结构是否正确及公式的指数Z值是否与实测值相符。大量的野外实测资料表明，式（6-22）的结构是正确的。在实验室内的研究方面，Vanoni（1946），Ismail（1952）及Einstein和钱宁（1955）等人做了大量的工作。他们的试验结果也都证实了式（6-22）的结构是正确的。但另一方面，实测的指数值Z1与式（6-23）的理论值Z之间仍有一定的差别。一般说来，Z1都小于Z。即实测的悬移质的垂线分布要比理论计算的结果更为均匀。Einstein和钱宁（1955）还从悬移质垂线分布的微分方程式推导了Z1和Z之间的理论关系，称之为扩散理论的第二近似解，如图6-3中的虚线。从图中收集的各种野外及室内的实测资料来看，当Z值较小时，实测值与理论值的差别不大，随着Z值的增加，两者的差距也越来越大，最后Z 1有接近于一个常数的趋势。

一种观点认为，悬移质扩散理论中的理论指数与实测指数不尽相符，这是由于在式（6-18）中假定泥沙扩散系数与动量交换系数相等的缘故。而实际上它们会有一定的差别。Vanoni从实验资料得出，泥沙扩散系数一般大于动量交换系数，据此假定

式中：β为大于1的比例常数，因泥沙的性质不同而异，则式（6-23）可以写成

图6-3　理论计算Z值与实测值Z 1的对比

从而可以与实测资料取得一致。

但是也有一些与此相反的结果，即β值小于1。例如Brush（1962）的试验结果。他在垂直向下的淹没射流中加入玻璃球，同时量测各断面的流速和含沙量的横向分布。结果表明，粒径为0.19mm的玻璃球的横向分布与流速分布一致，即β等于1，但对于两种较粗的球体（粒径为0.32mm和0.55mm），β值为0.50和0.15。作者认为这是由于粗颗粒泥沙的交换因受到惯性的影响，有落后于动量交换的情况。但若仔细分析其试验方法则可以看出，对于较粗的两种球体，由于沉速的影响，在相同的时间间隔内，玻璃球将比水团处于更低的位置，由于它们是向下呈扇形扩散的，越向下扩散得越宽，所以合理的方法应是取它们在同一时刻的分布作比较而不是取同一断面的分布作比较。如用这样的方法将会得出更大的β值。

Cellino（1999）从试验的实测资料得出，β值始终小于1（0.432～0.671），且与水流的饱和输沙程度有关，水流越趋近于饱和输沙，β值越小。需要指出的是，Cellino在用式（6-32）计算β值时，取k=0.4，但其实测资料的k值小于0.4。

Graf（2000）分析了大量的河流和水槽的实测资料得出，对于平整床面，β＜1，而对于有床面形态的水流，β＞1。

邵学军（1990）从泥沙颗粒的随机运动出发对扩散系数作了理论上的探讨，得出了一些有价值的结论。将颗粒在垂向上的位移速度分解为平均值和脉动值，平均值即为颗粒的沉速反号，即ω，脉动值取决于颗粒和流体的物理性质及紊动情况。颗粒的位移速度可近似地用伊藤随机微分方程表示

式中：Y（t）为颗粒的垂向随机位移；v′s为颗粒垂向速度的脉动强度；β（t）为布朗运动过程。(www.xing528.com)

式（6-33）可以改写成用白噪音过程α（t）表达的形式

采用上两式即是假定颗粒的垂向运动速度在相邻的两个时段中是互不相关的，而实际上运动颗粒的速度会有一定的相关时间TL，但如果主要研究时间尺度大于TL的情况，则上两式的假定是合理的。

试验资料和理论分析的结果表明，高频率小尺度的漩涡对颗粒的运动没有明显的作用，只有长度尺度大于或等于颗粒直径的紊动漩涡对颗粒的运动才是有效的，对应这种漩涡的时间比尺可表示为

式中：v′（y）为在高程y处长度尺度大于颗粒直径的那部分紊动漩涡的垂向脉动强度。根据雅林的观点，可以把流速脉动过程近似地表示为时间步长为tm的阶跃过程，如图6-4。在时段tm之内，点y处的脉动流速是恒定的，由颗粒在此恒定流场中的运动方程即可求出其速度v，再对不同的时段取统计平均就得到在统计平均意义下，颗粒在y处的垂向脉动强度为

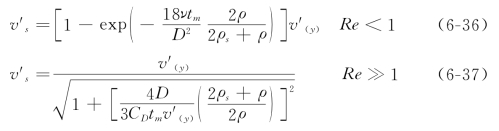
式中：CD为圆球绕流阻力系数。从统计物理学和随机过程的理论可知，非线性微分方程式（6-34）的解Y（t）所具有的转移概率密度P（y，t）应满足如下方程

图6-4　垂向流速脉动过程的简化模型

（a）实际过程；（b）阶跃过程

转移概率密度函数P（y，t）的物理意义是颗粒于时刻t0在点y0投放入紊动流场以后，于时刻t在y处出现的概率。若在时刻t0在点y0同时投放N个颗粒，则NP即表示时刻t在y处的颗粒浓度。设颗粒的密度相同，大小均匀，则NP与颗粒的体积浓度成正比，将式（6-38）的两边同乘以N，用体积浓度Sv代替NP，可得

对于浓度达到稳恒的情况，=0对y积分一次并利用浓度分布稳恒的条件可得

从上式与一般扩散方程相比即可得出

将式（6-35），式（6-36）及式（6-37）代入式（6-41），再根据试验资料定出常系数，取v′（y）≈u*，最后可以得出扩散系数的表达式

从上式可以看出，对于沉速处于紊流流区的颗粒，扩散系数将随粒径的加大而增加，但颗粒密度的影响较小。邵学军用专门设计的试验对式（6-42）进行了验证，见图6-5，图上还点绘了Rouse的试验结果，试验资料的粒径范围为0.125～0.95，比重为1.05～2.65。

图6-5　理论计算的扩散系数与实测值的对比

（三）扩散方程的修正

前已述及，式（6-22）的基本结构是正确的，但其计算的水面含沙浓度为零，床面处的浓度为无穷大，这与实际情况不符，其原因之一就是采用的动量交换系数是从对数流速分布公式推导而得的。

为了克服这一缺点，许多学者作了更进一步的研究。张小峰和陈志轩（1990）从悬移质扩散方程出发，根据粘性流体的非滑移条件，考虑了泥沙颗粒周围有部分流体随泥沙一起运动的特点，得出了一个新的悬沙浓度分布方程。在推导式（6-4）的时候，曾假定垂直方向的时均速度为零而得出了悬沙浓度的基本方程式（6-11）。张小峰和陈志轩认为，根据粘性流体的非滑移条件，泥沙颗粒表面的水体随泥沙颗粒一起运动，当泥沙颗粒以速度ω下沉时，其周围的部分水体亦将以ω或小于此值的速度向下运动，由连续条件可知，由于上升水体的体积减少，泥沙下沉引起的水体上升的速度将加大，则流体在垂直方向的时均速度应为

式中：m0为大于1的系数，它反映了颗粒表面附着水体的影响，与颗粒形状、尺寸及含沙量的大小等因素有关。相应式（6-14）的推导过程可以得出

式（6-44）与式（6-14）相比，多了一项含沙浓度的高阶项。假定泥沙扩散系数与动量交换系数成比例，取

将式（6-45）代入式（6-44）积分可得

从式（6-46）可以看出，在水面处，含沙浓度不为零，在床面处，当y趋于零时，由上式计算的含沙浓度为泥沙初始干容重与沙粒比重之比，这是合符实际情况的。可以看出，这一研究所依据的物理概念明确，所得结论合理，且公式结构简单，便于实际应用。此后，张小峰和谈广鸣（1992）又用相同的方法对非均匀沙的浓度分布进行了研究，得出了任一粒径组的悬沙浓度分布。

曹志先等（1995）从固液两相的连续方程和运动方程出发，当考虑两相混合体的质量通量时，得出混合体的垂向时均速度为

对比式（6-44）和式（6-48）可以看出，其结构形式相同但括号内的附加项反号。其主要差别在于垂向时均速度的选取，张小峰考虑泥沙下沉带动周围附着的水体下降，从而使液相有一个向上的时均运动，而曹志先则从流场的质量通量考虑得出混合流体具有一个向下的时均速度，导致了两个相反的结论。从研究问题的实质来看，混合流体在垂向上具有时均流动是难以成立的。

王兴奎和钱宁（1985）考虑了粒间离散力对浓度分布的影响，得出了扩散系数与颗粒直径、密度和浓度之间的关系。颗粒之间的碰撞将在垂直方向产生离散力，根据拜格诺的分析，离散力Pd可表示为

式中：λ为颗粒的线性浓度；ρm为浑水的垂线平均密度；k为浑水时均流速分布公式中的卡门常数。

当泥沙较粗，浓度较大时，颗粒离散力的影响已不能忽略，这一影响可以近似简化为使紊动流场中运动的颗粒的沉速降低。颗粒的群体沉速采用式（6-26），则当考虑了浓度和颗粒离散力影响后，式（6-32）中泥沙扩散系数的修正系数β值为

由式（6-49）和式（6-50）的结果表明，泥沙扩散系数将随粒径和密度的加大而增加，这是因为沙粒的比重越大、粒径越粗，其在紊动流场中运动的惯性越大，则会具有较大的扩散系数；此外，它还随含沙浓度的增加而加大，这是因为颗粒离散力随浓度加大而加大，其综合作用是使悬沙的垂线浓度分布更均匀。这些结论与邵学军的理论分析结果有相同之处。图6-6是计算结果与爱因斯坦和钱宁及王兴奎和钱宁的实测资料的对比，从图中可以看出，计算值与实测值的符合程度是令人满意的。

图6-6　计算浓度分布与爱因斯坦和钱宁（a）及王兴奎和钱宁（b）实测值的对比