Samaga的研究探索与创新

Samaga等人（1986）在长30m，宽0.20m的变坡循环水槽中，用四种混合沙进行了系统试验。试验条件为：D50=0.25～0.57mm，几何标准差σg=1.91～3.41，水深h=0.06～0.11m，平均流速U=0.49～0.78m/s，坡度J=0.005～0.007，推移质单宽输沙率gb=1.08～5.78N/（m·s）。在试验时，等水沙平衡以后，量测中垂线的流速分布U—y和浓度分布，沙样颗分后定出各级泥沙的垂线分布Ci—y，CiU积分即得出第i级粒径的悬移质输沙率。在水槽出口取样得出总的输沙率，作颗分后可得出各级泥沙的总输沙率，扣除相应的悬移质输沙率后就可得出各级粒径的推移质输沙率。

在进行资料分析时，建立分级输沙强度Φi与沙粒剪应力τ′o对应的Shields数Θ′i[τ′o/（γS—γ）Di]之间的关系，如图5-28，在图中同时画出了D=D50的均匀沙的关系曲线。

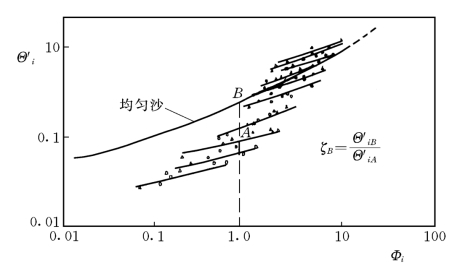
图5-28　分粒径级的输沙率参数Φi与Shields数Θ′i的关系

从图中可以看出，在相同的水流条件下，细粒径组（均匀沙曲线上部）的输沙率小于均匀沙的值，而粗粒径组（均匀沙曲线下部）的输沙率则偏大。定义在某一输沙强度下，Di粒径组的Shields数Θ′i与相同粒径均匀沙的Shields数Θ1的比值ζB为隐蔽——暴露系数，如图5-28中的ζB即定义为Θ′B与Θ′A的比值。由试验发现，Θ′i还和泥沙的均匀系数M有关，均匀系数定义为：在直角坐标的级配曲线中，从50%画一条横线，级配曲线上方小于50%的面积与大于50%的面积之比，如图5-29中面积B与面积A之比。M对Θ′i的影响可用系数LB表示，其相互关系见表5-2。点绘ζBLB与Θ′i的关系发现，随τ′0/τoc的变化，ζBLB与Θ′i遵循不同的关系。如用KB表示τ′0/τoc的影响，见图5-30，则KBζBLB的乘积与Θ′i遵循统一的规律，见图5-31。这样，由表5-2及图5-30和图5-31，已知分粒径级的Θ′i就可求出相应的ζB，最后得出ζBΘ′i与Φi的统一规律，见图5-32。

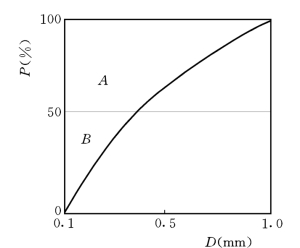
图5-29　均匀系数M定义

表5-2　LB随M的变化

(www.xing528.com)

图5-30　KB与τ′0/τ0c的关系（只与水流条件有关）

实际计算过程归纳为：从级配曲线求出M，由表5-2内查得出LB，根据水流条件由图5-30查出KB，已知分粒径级的Θ′i，由图5-31查出KBζBLB的值，计算出ζB值，最后用ζBΘ′i由图5-32查出Φi值，由Φiib的值从式（5-48）即可算出分粒径级的输沙率，求和即得出总输沙率。图5-31和图5-32的资料包括室内试验和野外观测的资料。

图5-31　KBζBLB与Θ′i的关系

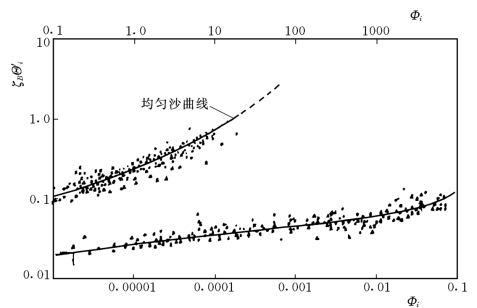
图5-32　分组粒径输沙率的统一关系

惠遇甲（1992）对有关非均匀沙挟沙力的研究成果进行了全面的总结和评述，列出参考文献50余篇。