Einstein的质运动理论推移（1942，1950）

Einstein从长期的实验观察中注意到床面泥沙颗粒的运动具有随机性，推移质与床沙之间存在着不断的交换，根据这些物理图形，运用现代流体力学的知识建立了推移质运动的理论。并用实测资料建立了推移质运动强度Φ与水流参数Ψ之间的经验关系。以后又利用概率论的方法导出了Φ和Ψ函数关系的数学表达式，并进一步推广到非均匀沙。最后又从推移质和悬移质之间同样存在交换的概念出发，把推移质运动理论和悬移质扩散理论联系起来，提出了床沙质挟沙力的计算方法。这一方法就现阶段的水平而言，是考虑最全面的方法之一。

（一）床沙与推移质之间的交换现象

试验观测的结果表明，床沙与推移质之间存在着交换。对于任何一颗推移质泥沙来说，它的运动行程是间歇的，而不是连续的。它在被水流搬运一段距离后，便在床面静止下来，成为床沙质，其运动过程示意如图5-13。可以认为，推移质输沙率实质上决定于泥沙颗粒在交换过程中在床面停留时间的久暂，停留时间越长，推移质输沙率越小。

（二）交换现象的统计分析

研究推移质的运动规律，最好是用统计的方法研究大量的泥沙颗粒在一定的水流条件下的运动规律。在Einstein的染色沙试验中，从处于平衡状态的河段的进口在某一时段投入染色沙粒，观测这些沙粒在不同时间在床面的分布，结果如图5-14所示。这一图形与弹子盘中弹子的运动轨迹十分相似，根据这一模式，对推移质泥沙运动得出了如下基本认识：

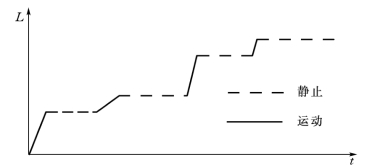
图5-13　卵石推移质颗粒的运动过程

图5-14　床面染色沙粒的分布

1）河床表面的泥沙和运动的推移质之间存在着不断的交换。

2）应该采用统计学的观点来研究大量的泥沙颗粒在一定的水流条件下的运动过程。

3）任何泥沙颗粒自床面被水流带起的或然率决定于泥沙的性质及床面附近的流态，而与其过去的历史无关。使泥沙运动的作用力主要是上举力，当瞬时上举力大于泥沙颗粒的水下重量时，床面泥沙进入运动状态。

4）泥沙颗粒运动的单步距离约为沙粒直径的100倍。

5）泥沙在床面上各处落淤的或然率相同。

（三）推移质公式的推导

推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。

1.泥沙的沉积率

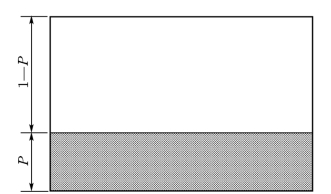
图5-15　水流上举力大于沙粒水下重量所占床面比例示意图

在一定的水流条件下，假定河床表面比例为P的部分面积上的水流上举力大于泥沙颗粒的水下重量，有1—P的面积上的上举力小于泥沙的水下重量，示意如图5-15。当进入研究断面的N颗沙粒走完一个单步距离后，将会有N（1—P）颗沙粒正好落在水流的瞬时上举力小于泥沙的水下重量的面积上而沉积下来，另有NP颗沙粒落在瞬时上举力大于泥沙的水下重量的面积上，则走完一个单步距离后再继续前进。在完成第二个单步距离后，又有NP（1—P）粒沙沉积下来，再剩下NP2颗泥沙继续前进，如此不断发展下去，当走完第K个单步距离后，会有NPk—1（1—P）颗沙沉积下来，最后可得泥沙运动的平均距离为

若推移质泥沙的单宽输沙率为gb，则在单位时间内通过所研究断面的泥沙，都将在长度为L0的范围内沉积下来，这样，单位面积上泥沙的沉积率gd为

2.泥沙的冲刷率

泥沙颗粒自床面冲刷外移的条件取决于有多少这样的泥沙暴露在水流下面，及使泥沙举离床面的上举力大于沙粒水下重量的或然率有多大。假定在单位面积上的泥沙颗粒数为，则其重量为。根据前面的假定，在单位床面面积上，有比例为P的面积上的水流上举力大于泥沙的水下重量，即颗粒冲刷外移的或然率为P。这样，在单位面积上，将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。

已知冲刷外移的沙量，需要进一步求出这些泥沙被冲走的时间，假定泥沙的交换时间与泥沙在静水中沉降一个粒径的距离所需的时间成正比，即

最后得出单位面积上泥沙的冲刷率gS为

前已述及，使泥沙冲刷外移的或然率定义为水流的上举力大于泥沙颗粒水下重量的概率，则其有两种含义，对同一床面面积上的不同时刻，它代表在全部时间中泥沙被冲刷外移的时间比例；对同一时刻的单位床面面积，它则表示上举力大于泥沙水下重量的面积比例，所以在泥沙沉积率和泥沙冲刷率中的或然率P是同一物理量的不同表达方式。

3.输沙平衡条件(www.xing528.com)

当推移质运动达到平衡时，自河床冲起的泥沙和推移质中落淤的泥沙应相等，则

Φ为推移质运动强度，或然率P为

泥沙的水下重量为

水流作用在颗粒上的上举力为

Einstein（1949）从试验结果得出，若取距理论床面0.35D处的流速作为上式中的有效流速，CL=0.178，上举力的脉动遵循正态分布

式中：η为随时间而变化的上举力脉动值，如用上举力脉动的标准差η0来衡量上举力的大小，即令η=η0η*，其中η*为无量纲的上举力脉动值，再令

或然率P代表W′/FL小于1的机遇

由于上举力与流速的平方成正比，不管流速是正或是负，上举力总是正的，见图5-16，所以式（5-55）可以写成绝对值的形式

图5-16　推移质运动概率（图中阴影部分）示意图

令B*=B′/η0，对泥沙颗粒刚好被举离床面的临界状态

在这一范围内，上举力小于泥沙颗粒的水下重力，不会有推移质运动。前已假定，上举力的分布为正态分布，则η*的分布也应是正态的，即

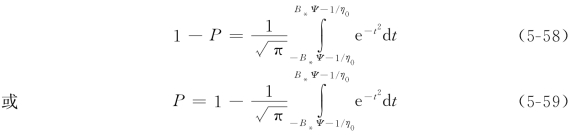
最后可得推移质输沙率公式

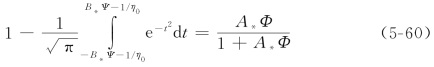
式中的常数可根据试验资料确定：η0=0.5，A*=1/0.023，B*=1/7。理论公式与试验资料的对比见图5-17，由图可知，两者是十分相似的。

图5-17　爱因斯坦推移质公式与试验成果的对比

在爱因斯坦的公式中，Φ与Ψ为积分关系式，不便于实际应用，爱因斯坦给出了Φ与Ψ的关系图供查用，如图5-18。在实际计算时用下式计算亦有足够的精度。

必须注意，由式（5-54）计算Ψ时应采用R′b。