床面形态等效糙度法

Simons和Richardson曾提出过当量糙率（Equivalent Roughness）的概念，其后van Rijn（1982）、Brownlie（1983）、秦荣昱（1987）等研究者都对运用当量糙率计算冲积河流阻力的方法进行了研究。

（1）Brow nlie方法。Brow nlie（1983）从量纲分析出发，根据大量实测与试验资料，提出了一个沙质河床低速流区和高速流区的水深预报方法。这个方法对于数值模拟计算来说，应用比较方便。在Brownlie的方法中，并未将水流阻力划分为沙粒阻力和沙波阻力。虽然仍考虑了床面形态的作用，但却是将其作为大尺度的颗粒或当量糙率来处理的。泥沙颗粒特性由中值粒径D50、比重γs=ρsg，以及几何标准偏差σg（假定粒径属于对数正态分布）三个变量来描述。这种方法中的无量纲组合参数为

式中：无量纲单宽流量；σg和D50反映泥沙级配的影响。

式（3-109）中假定水流在完全粗糙区，Reynolds数的大小不引起阻力系数变化，所以自变量中将Re排除在外。

对于沙垄床面上的水流，综合阻力系数可按半对数方程或其近似的幂次表达形式表示（类似于Manning-Strickler公式），但粗糙高度由测量的河床形态高度kd代替，即

式中：a为比例系数。

对上式进行一系列繁复的整理，最终得到

式（3-111）表明，Shields数Θ与kd的0.1次幂成比例，因此Θ并不明显取决于kd，或者说kd的精确度并非Θ的决定性因素。进一步假定κd/D50与未确定幂次的q*J成比例，床沙非均匀性的影响由σg的幂次来体现。将这些假定代入式（3-111）有

式中：β，x，y，z均为未知常数，对上式两边取对数后，通过多元回归可确定这些常数。Brownlie分别将22组试验和实测系列的1100多组数据区分低能态和高能态后，点绘了它们的最佳拟合关系，如图3-34和图3-35。其相关系数分别为R=0.992和R=0.999。

经过回归分析，Brownlie建议，对于宽浅河流，h=R，低水流能态区的水深可用下式确定

图3-34　低水流能态区（沙纹和沙垄）Θ和q*、J的关系（Brow nlie，1983）

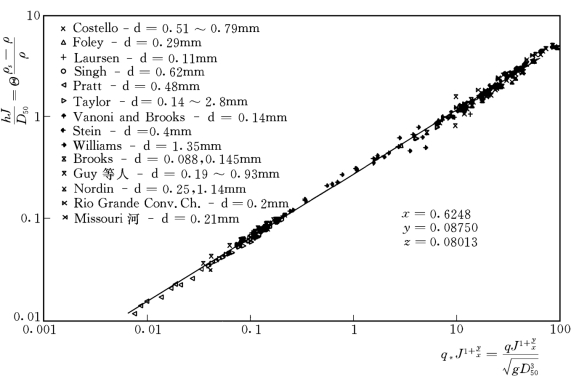
图3-35　高水流能态区（动平床，逆行沙浪）Θ和q*、J的关系（Brow nlie，1983）

对于高水流能态区，可用下式确定

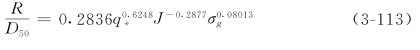
对于水流流区的确定，Brownlie选用无量纲参数Fg、D50/δ和比降J。其中

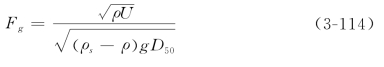
是沙粒Froude数，其意义为作用于沙粒上的拖曳力与其水下重量之比的平方根。参数D50/δ为平均粒径与粘性底层厚度的比值，其中δ为粘性底层的厚度，δ=，变量是由方程（3-114）得到的高速流区无沙垄时的剪切流速u*。

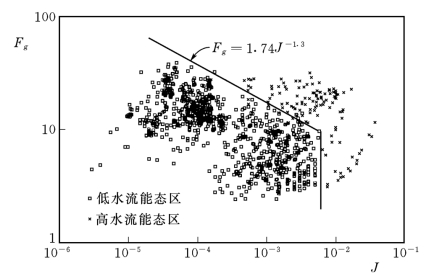
根据沙粒Froude数Fg和比降J所绘的流区关系如图3-36和图3-37。

(www.xing528.com)

图3-36　水流高、低能态判别图（Brow nlie，1983）

从图3-36和图3-37中可以看到，当比降J＞0.006时，只存在高能态流区；对于较小的比降J，可按下列方程给出一个近似的分界线

符号特指该线上的Fg值。对于沿该线的交迭的过渡区，可由下两式确定：

1）低速流区的上限方程

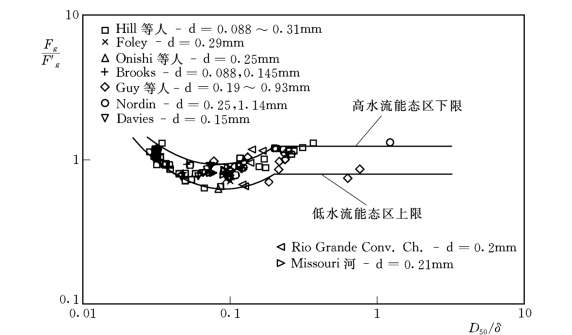
图3-37　过渡区水流能态判别图（Brow nlie，1983）

2）高速流区的下限方程

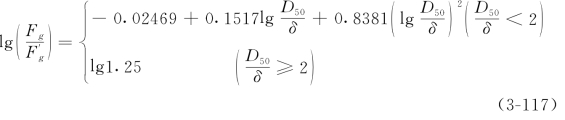
（2）van Rijn方法。荷兰工程师van Rijn（1982，1984a，1984b）研究了床面形态特征、Chezy系数与水流以及床沙参数间的关系，根据较为可靠的1500组水槽和实测资料，提出了计算河床形态尺寸和有效水力粗糙度的计算方法。如第三章所述，他把低能态和过渡区所形成的床面形态类型表示成无量纲输运强度参数T和无量纲粒径d*的函数，从而建立沙波尺寸和它们的有效粗糙度的简单函数关系

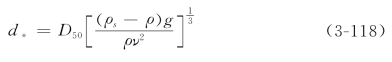
式中：ν为动力粘滞系数；u*C为Shields临界河床剪切速度，其计算式为（van Rijn，1984a）

其次，通过分析大量水槽和现场资料，导出沙波波高Δ和波长λ的计算式如下

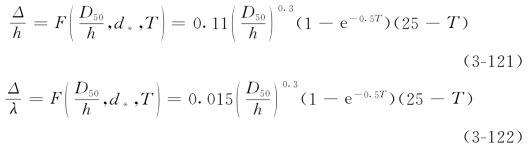
van Rijn认为动床粗糙度是由颗粒糙度ks颗粒和形状糙度ks形状引起的。通过研究导得

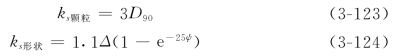
其中沙波陡度ψ=Δ/λ，当Δ/λ=0时即为平床。

于是高、低能态和过渡区（除逆行沙波外）的动床有效粗糙度ks可用下式计算

最后得到Chezy系数为

【注释】

[1]姜国干，1948，水槽两壁对于临界拖曳力之影响，中央水利实验处研究报告乙种1号。