综合糙率与河床及河岸糙率的关系处理方法

明渠流动的边界剪切应力中，记河岸部分的剪切应力为τw，河床上的剪切应力为τb，过水断面湿周中河岸部分为Pw，河床部分为Pb，如图3-24。

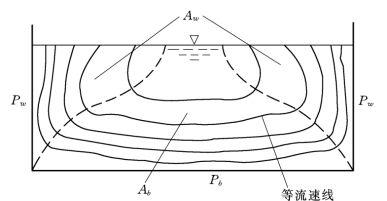
图3-24　Einstein的水力半径分割法

对于恒定均匀流动来说，分析隔离水体上的受力平衡，可求得全断面（总湿周长为P）上的边界剪应力平均值为τ0=γRJ，因此应有

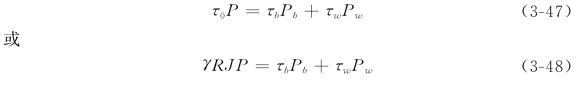
通常情况下的已知量包括Q、J、Pw、Pb、P、边壁糙率nw和床面糙率nb。水深h和水力半径R一般是未知量，需要求解。求解时必须给出τb和τw的表达式以使阻力方程组封闭，也就是将边界中的河岸边壁和床面区分开来计算各自的剪切应力。据此推求综合糙率n，最后就可用Manning公式解算水深。

给出τb和τw的表达式的方法有两种，一种是由Einstein（1942）提出的水力半径分割法，另一种是能坡分割法。这两种方法可以通过以下的解析理论进行对比和分析。

（一）综合糙率处理方法的解析分析

Einstein将整个过水面积划分为3个区域，如图3-24所示。他认为各个区域内的水体机械能只传递到本区域的边界上，且各个区域内能坡可以看作是相同的。在这些假定下，河床、河岸阻力可写成

以下的分析中，以不带下标的参数表示相应于全断面的参数，下标为“b”的参数表示相应于河床床面的参数，下标为“w”的参数表示相应于河岸边壁的参数。

朱鹏程（1991）对峡谷河道边壁糙率进行分析时，从阻力方程组解的惟一性出发推导得到了Einstein综合糙率系数关系式。随后许光祥（1996）在分析河床阻力和河岸阻力的问题时，也从类似思路出发对综合糙率系数关系的不同处理方法进行了研究。许光祥令已知参数为A、U、J、Pw、Pb、nw、nb，未知参数为Ab、Ub、Rb、Aw、Uw、Rw、n。这样运用式（3-49）、式（3-50）求河床阻力τb和河岸阻力τw时总共需要列出7个方程，合称为阻力方程组。它们可由几何形态连续、水流连续、水力半径定义、曼宁公式及经验或半经验公式等方程组成，除全断面Manning公式（3-37）外，还可写出5个方程（含河岸、河底各自的Manning公式）如下

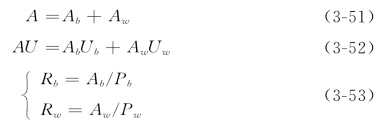
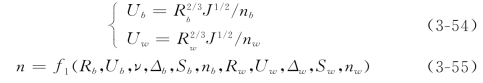
按许光祥定义，式（3-55）中的Sb、Sw分别为与河床阻力及河岸阻力相联系的水体的形状系数；Δb、Δw分别为河床及两壁的绝对糙度；ν为水流的运动粘性系数。至此方程数已达6个。由于河岸、河床可以看成是定床，它们的糙率可以通过经验方法或其他方法确定。但综合糙率不易预先确定，即阻力方程组中的式（3-55）实际上为未知关系，也就是还缺少一个定解条件，需要补充一个方程。由于J、Pw、Pb是已知量，由式（3-49）、式（3-50）和式（3-53）可以看出，求解河床阻力τb和河岸阻力τw实际相当于求解Aw。许光祥将Aw作为自变量，不作任何假定或附加条件，列出求解Aw的方程。根据各个阻力单元的曼宁公式，有

利用式（3-56），可将式（3-52）改写为如下形式

将式（3-51）和式（3-53）代入式（3-57），写成Aw的函数形式，则得到含Aw和n两个未知数的方程如下

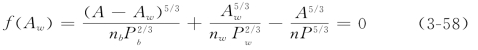
求解Aw就相当于求方程（3-58）的根。因为方程中n也是个未知数，许光祥（1996）认为可以通过判断方程是否有解，来把n表达为nb和nw的恰当形式，从而获得综合阻力的处理方法。将f（Aw）对Aw求一阶和二阶导数，可得

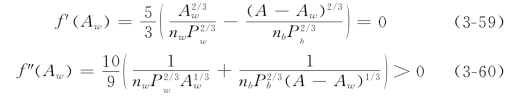
如果能找到令f′（Aw）=0且f″（Aw）＞0的点，就可知函数f（Aw）有极小值点存在。为此解方程f′（Aw）=0，可得到令f（Aw）取极小值的惟一的一个Aw值是

在x oy坐标系内，令y=f（Aw），x=Aw，则方程（3-58）有解的几何意义就是曲线y=f（Aw）与横轴存在交点。因为函数f（Aw）有极小值，所以只有当此极小值小于零时，曲线y=f（Aw）与横轴才存在交点，方程（3-58）才有解。换句话说，如果把式（3-61）给出的Aw值代入方程（3-58），应有

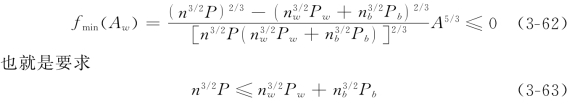
这就是封闭阻力方程组所需要的最后一个条件。根据条件式（3-63），可以看出阻力方程组解的存在性与Einstein（1942）提出的水力半径分割法和姜国干提出的能坡分割法之间的关系。

（二）水力半径分割法

Einstein认为水体分几部分与各相应边界上的剪切力分别平衡，并作了如下假定：全断面能坡J相同，各分区流速都相同，而且能使用Manning公式（3-37）分别计算。Einstein所给出的τb和τw的表达式是式（3-49）和式（3-50），代入式（3-48），约去J和γ后得

根据Einstein的假设，各分区流速都相同，使用式（3-37）分别计算有

由此得到R，Rw和Rb的表达式分别为

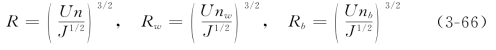
其中n，nw和nb都是已知量。代入式（3-64）中可得

化简后得到综合糙率的表达式

比较式（3-63）和式（3-68），很明显，Einstein对综合阻力的处理方法就是使式（3-63）的等号成立。所以，Einstein的处理方法事实上是前述阻力方程组存在惟一解的必要条件。根据这一理论推导，用Einstein法求得的综合阻力系数n，是所有能使阻力方程组有解的n值中的最大值。此时，Aw的解为式（3-61）。

朱鹏程（1991）的分析也从式（3-57）出发进行。他分别利用各分区流速都相同和能坡都相同这两个假设，加上面积恒等或流量恒等的关系，给出了综合阻力系数n的两个表达式，也即求解得出了式（3-55）的函数式。将两式分别对Rb求导可得到n的两个极值条件，由这两个条件均可得出式（3-68）。两个极值中一个是极大值、一个是极小值，而且两条曲线在极值点相切、n的值相同即是一个惟一解，由此亦推出Einstein法是阻力方程组存在惟一解的必要条件。

由式（3-68）可见，当河道十分宽浅时（Pw≪P），综合糙率主要由nb所决定。

推论 由流量叠加原理和各分区流速、坡降都相同的假设出发，有(www.xing528.com)

代入Manning公式（3-37）得到

约去坡降J后可得式（3-57），从而得到综合糙率的另一种表达式

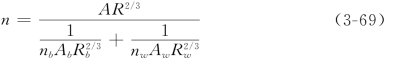
在河流模拟的一维数学模型中有时要用到这个结果。

又因为A=RP，Aw=RwPw，Ab=RbPb

代入式（3-57）后得到综合糙率与边壁、河床糙率的关系为

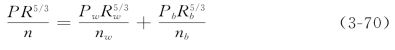
这两种方法都用到了全断面能坡J相同，各分区流速都相同的假设。

Einstein的水力半径分割法的物理含义，是认为一段边界上产生的紊动，只能影响该边界附近的水流，而不能传播到全断面，这也就是要求没有贯穿整个断面的大尺度紊动。显然，对于河道边界粗糙突起不太大、或者平原宽浅河流的情况来说，这个假设是合理的。此外，他所作的岸壁区、河床区水流速度相同的假设，也是只在类似的情况下才可认为是合理的。

（三）能坡分割法

在一定的河道条件下（如边界粗糙突起与水流的特征尺度相比已相当大，或断面形状比较窄深），一段边界上产生的紊动，不仅影响该边界附近的水流，而且能传播到全断面。此时由于岸壁所产生的紊动与床面所产生的紊动在全断面上完全混合在一起，不能区分，可以假定全断面水流共同平衡边壁和河床的剪切力，而不是区分成几个部分分别与各边界单元平衡。但水流消耗的总能量仍可区分成两部分，一部分消耗于岸壁所产生的紊动，另一部分则消耗于河床床面所产生的紊动。从能坡分割法的角度来说，总能坡中一部分与岸壁剪应力平衡，另一部分用来与河床剪应力平衡。能坡分割法所给出的τb和τw的表达式是

代入式（3-48）可得

将Manning公式分别用于岸壁区和河床区，反算出Jw和Jb代入上式，有

如果设水流满足如下较强的条件（全断面流速相同，不区分水力半径）

由此可以得到

也可以设水流满足如下较弱的条件（全断面流速不相同，区分水力半径）

同样可得到式（3-74）。由式（3-74）可得综合糙率的表达式为

这就是姜国干（1948）^[1]根据能坡分割法得到的结果。与Einstein方法得到的式（3-68）相比，式（3-75）中nw、nb是平方后加权平均，而在式（3-68）中两者是1.5次方后再加权平均，可见在其他条件相同的情况下，式（3-75）的结果倾向于令较大的糙率值占较大的比重，也就是略微突出了较大的粗糙所产生的紊动对阻力的贡献。

能坡分割法与阻力方程组解存在条件的关系。许光祥（1996）指出，能坡分割法不能满足前述阻力方程组有解的条件，因为这一方法给出的综合阻力系数n值，总是大于用Einstein法求得的综合阻力系数n值（而这个值已经是容许的最大上限），可分析如下。

将能坡分割法求得的综合阻力系数记为nJ，Einstein法求得的综合阻力系数记为nE，将式（3-68）和式（3-75）改写为如下形式，

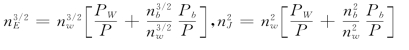
引入如下符号：Z=nb/nw，C=Pb/P，1—C=PW/P，Y=（nJ/nE）2，则可以写出

分析可知，上式所确定的Y值随Z而变，当Z=1时Y存在一个极小值Ymin=1，此外对于任何其他Z值均有Y＞1，即nJ＞nE。所以，采用能坡分割法，只有在nb=nw这种特殊情况时，才满足阻力方程组有解条件，此时水力半径分割法和能坡分割法会得到相同的结果。因此，从上述解析分析的角度出发，水力半径分割法更为严密一些。

（四）综合阻力的其他处理方法

Darcy-Weisbach公式的应用。由Darcy-Weisbach公式（3-39）可得，因此可将式（3-48）写为

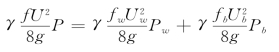
因此，无论用水力半径分割法还是用能坡分割法，只要设U=Uw=Ub，即可得到综合的Darcy-Weisbach阻力系数表达式

相应于N组断面分区的情况，也可得到

可见，如果公式的系数是无量纲的，在作代数演算时会有不少的便利。但正因为它是无量纲的，它的影响因素中必然包含水流的尺度（例如Reynolds数这个无量纲数就含有水流的特征长度）。因而Darcy-Weisbach系数不仅与边界粗糙程度有关，还与水深有关，虽然公式简单，但其值的确定并不简单。而有量纲的Manning粗糙系数n，与粗糙突起ks一样，在于恒定、均匀、定床的明渠流动中，对一个特定的边界只取一个特定值，可以认为它不随水深而变，所以公式虽略为复杂，但计算过程比较简单。

按上述方法求得全断面综合粗糙系数n，f后，就可按Manning公式（3-37）或Darcy-Weisbach公式（3-39）确定水位—流量关系。